开心洋葱 , 版权所有丨如未注明 , 均为原创丨未经授权请勿修改 , 转载请注明(Python)从零开始,简单快速学机器仿人视觉Opencv—运用五:物体运动跟踪!
(Python)从零开始,简单快速学机器仿人视觉Opencv—运用五:物体运动跟踪

-
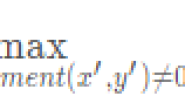
OpenCV图像处理视频教程——入门篇(二) -
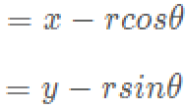
OpenCV图像处理视频教程——入门篇(三) -
在ubuntu18.04中安装opencv_contrib-3.2.0采坑教程 -

(Python)从零开始,简单快速学机器仿人视觉Opencv—运用一:快速截取图像中指定单个物体
- (Python)从零开始,简单快速学机器仿人视觉Opencv—运用三:物体运动跟踪
- 基于MATLAB的图像处理笔记
- (Python)从零开始,简单快速学机器仿人视觉Opencv—第二节:OpenCV的视频操作
- OpenCV学习+常用函数记录①:图像的基本处理
- OpenCV学习+常用函数记录②:图像卷积与滤波
- (Python)从零开始,简单快速学机器仿人视觉Opencv—第三节:OpenCV中的绘图函数
- (Python)从零开始,简单快速学机器仿人视觉Opencv—第四节:OpenCV处理鼠标事件
- (Python)从零开始,简单快速学机器仿人视觉Opencv—第五节:OpenCV用滑动条做调色板
- (Python)从零开始,简单快速学机器仿人视觉Opencv—第六节:OpenCV图像的一些基本操作
- (Python)从零开始,简单快速学机器仿人视觉Opencv—第七节:图像上的算术运算
- 数字图像处理(一) 绪论
- 数字图像处理(二) 数字图像处理基础
- 数字图像处理(三) 图像的变换
- 计算机视觉实战(二)图像基本操作
- (Python)从零开始,简单快速学机器仿人视觉Opencv—第十四节:图像梯度
- (Python)从零开始,简单快速学机器仿人视觉Opencv—第十六节:图像金字塔
