反向传播

  前面讲解了卷积神经网络的网络基本架构。我们在实际运算的时候会发现，随着计算次数的增加，我们的输出结果与我们的预期结果会不断的逼近。这是因为网络中的权重参数在不断的调整，那么参数是如何调整的？这就涉及到一个反向传播的问题。反向传播其实是神经网络的一个基础，下面我通过一个简单的示例带大家详细了解一下这个数学过程。  

前向传播过程

  了解反向传播之前，我们先来简单回顾一下前向传播的过程。也就是神经网络正常走完一个周期的过程。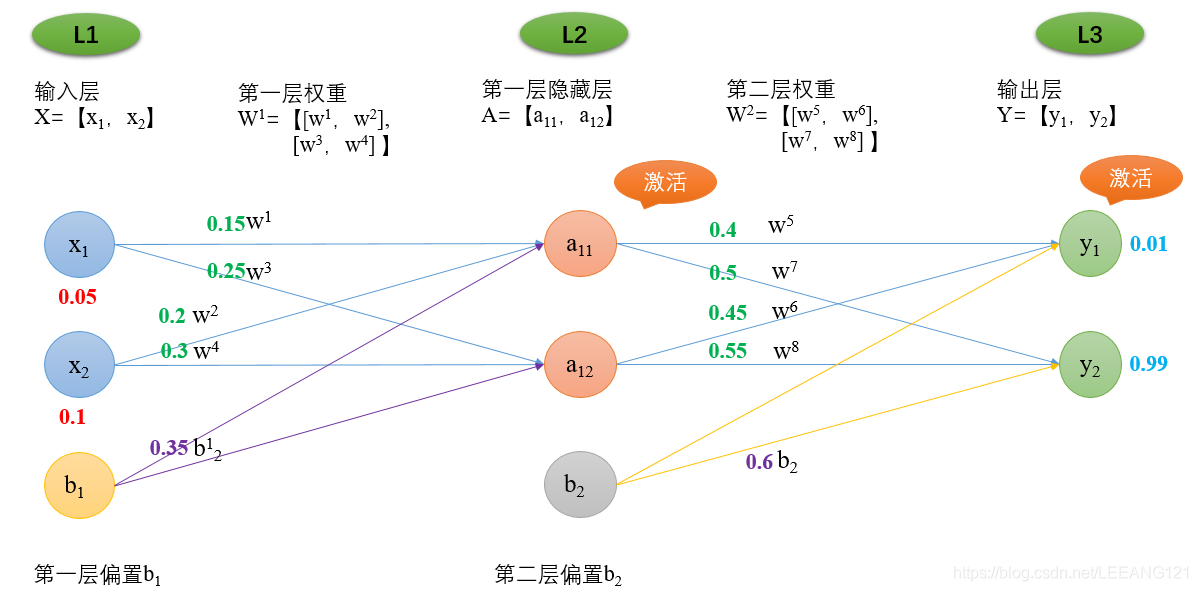  
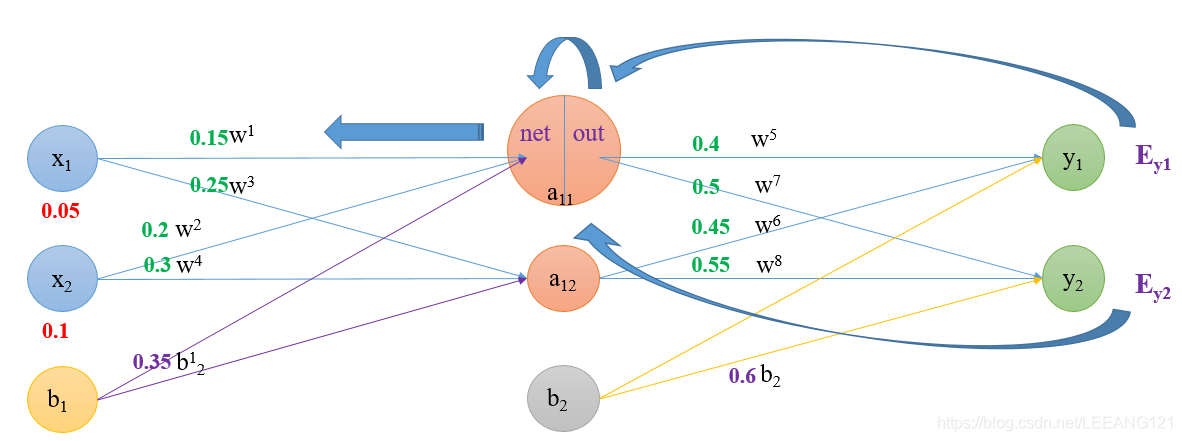
  如图所示，这是典型的神经网络的基本构成。其中L1层是输入层，L2层是隐藏层，L3层是输出层。假定我们现在输入一系列数组，我们希望最后的输出是我们预期的值，那么这些数组必然要经历一个参数的计算过程，下面我们通过一个具体的示例讲述一下这个变化是如何发生的。   首先我们明确初始条件   输入数据：x 1 = 0.05 ; 输出数据：y 1 = 0.01;   初始权重（随着计算的进行，权重会不断的更新迭代）：w 1 = 0.15 , w 2 = 0.2 , w 3 = 0.25 , w 4 = 0.3 , w 5 = 0.4 , w 6 = 0.45 , w 7 = 0.5 , w 8 = 0.55 ;   偏置：b 1 = 0.35 , b 2 = 0.6 .   激活函数为sigmoid函数(用激活函数是为了去线性化，具体原因我会在下次笔记中介绍）   这个神经网络的目的就是，我们给出一组输入，最后使得输出尽可能的接近y 1 = 0.01 , y 2 = 0.99 .   现在开始前向传播   （1）从L1层到L2层(输入层到隐藏层)：   计算神经元x 1​的输入加权和：n e t a 11 = w 1 ∗ x 1 + w 2 ∗ x 2 + b 1 ∗ 1    带入数据：n e t a 11 = 0.15 ∗ 0.05 + 0.2 ∗ 0.1 + 0.35 ∗ 1 = 0.3775    神经元a 11 的输出为（对神经元执行一次sigmoid激活）：  
  同理可得a 12的输出为：o u t a 12 = 0.596884378    (2)从L2层到L3层（隐藏层到输出层）：   （此时的L2层相当于我们的输入层，计算过程类似上一层）   计算输出神经元y 1 的输入加权和：n e t y 1 = w 5 ∗ o u t a 11 + w 6 ∗ o u t a 12 + b 2 ∗ 1   带入数据：n e t y 1 = 0.4 ∗ 0.593269992 + 0.45 ∗ 0.596884378 + 0.6 ∗ 1 = 1.105905967   
  同理可得y 2 ​的输出为：o u t y 2 = 0.772928465    这样前向传播的过程就结束了，我们得到的输出值为[0.75136507 , 0.772928465]，与实际值[0.01 , 0.99]相差还很远，为了得到一组接近我们需要的数据，我们需要调整参数（神经网络的权重），重新计算输出。那么如何调整参数？我们应该知道当前参数对误差的总影响，具体的方法就是要进行反向传播计算。

反向传播过程

  在进行反向传播之前，我们最后再回顾一下我们刚刚做了什么事情。 1,刚刚，我们首先定义了一组输入数值X ;   2,我们对输入数组执行第一册计算并将结果给到了隐藏层L2，我们假定这个函数为F ( x ) ;3,我们对隐藏层进行了非线性处理，假定这一步操作为S ( F ( x ) ) ;   4,接着我们将L2层视为新的输入层，对他执行了一系列变化并将值给到输出层L3，假定这一步操作为G ( S ( F ( x ) ) ) ;   5,最后我们对输出层执行了非线性变化，得到第一次计算的最终结果，这一步操作可以看做T ( G ( S ( F ( x ) ) ) ) .   6,根据链式法则，现在我们要做的就是给这个多嵌套的函数脱衣服。。。   脱衣服的过程一定要遵循先穿的后脱，后穿的先脱（会不会被河蟹）。。。   开始脱衣服反向传播：   1，计算总误差：  
  因为有两个输出，所以分我们别计算$y1$和$y2$的误差，然后计算两者之和：  
 

输出层向隐藏层的权值更新：

  以权重参数w5为例，如果我们想知道w5对整体误差产生了多少影响，可以用整体误差对w5求偏导求出：（链式法则）  
 
  我们来计算每一个单独的算式：  
 

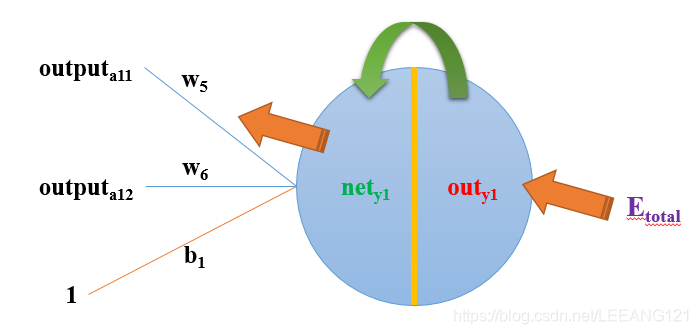
隐藏层向输入层的权值更新

  计算方法与上面一样，但是需要注意一点。从L3层到L2层计算权重w 5 时，是从o u t y 1 到n e t y 1 再到w 5​；而从L2层到L1层就算权重w 1 （以w 1 为例），是从o u t a 11 到n e t a 11​再到w 1 ​,其中o u t a 11 ，其中o u t a 11 ​接受的是从E y 1 和E y 2 两个方向传递的影响。  
  其中：  
 
 
 
  这样误差反向传播法就完成了，最后我们再把更新的权值重新计算，不停地迭代，在这个例子中第一次迭代之后，总误差E(total)由0.298371109下降至0.291027924。迭代10000次后，总误差为0.000035085，输出为0.015912196,0.984065734,非常接近预期输出，证明效果还是不错的。   传送门： CNN卷积神经网络原理详解（上） CNN卷积神经网络原理详解（中）