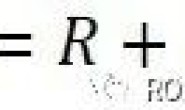@[toc]
一、ORB特征
1.1 FAST关键点

- 选取像素p,假设它的亮度为Ip;
- 设置一个阈值T(比如Ip的20%);
- 以像素p为中心,选取半径为3的圆上的16个像素点;
- 假如选取的圆上,有连续的N个点的亮度大于Ip+T或小于Ip-T,那么像素p可以被认为是特征点;
- 循环以上4步,遍历每一个像素执行相同操作。
1.2 BRIEF 描述子
论文:BRIEF: Binary Robust Independent Elementary Features
BRIEF算法的核心思想是在关键点P的周围S*S大小的范围内以一定模式选取N个点对,把这N个点对的比较结果组合起来作为描述子。为了保持踩点固定,工程上采用特殊设计的固定的pattern来做。
详细可以看:https://www.cnblogs.com/long5683/p/9737510.html
ORB_SLAM中定义的pattern
//下面就是预先定义好的随机点集,256是指可以提取出256位的描述子信息,每个位由一对点比较得来;4=2*2,前面的2是需要两个点(一对点)进行比较,后面的2是一个点有两个坐标
static int bit_pattern_31_[256*4] =
{
8,-3, 9,5/*mean (0), correlation (0)*/,
4,2, 7,-12/*mean (1.12461e-05), correlation (0.0437584)*/,
-11,9, -8,2/*mean (3.37382e-05), correlation (0.0617409)*/,
7,-12, 12,-13/*mean (5.62303e-05), correlation (0.0636977)*/,
2,-13, 2,12/*mean (0.000134953), correlation (0.085099)*/,
1,-7, 1,6/*mean (0.000528565), correlation (0.0857175)*/,
-2,-10, -2,-4/*mean (0.0188821), correlation (0.0985774)*/,
-13,-13, -11,-8/*mean (0.0363135), correlation (0.0899616)*/,
-13,-3, -12,-9/*mean (0.121806), correlation (0.099849)*/,
10,4, 11,9/*mean (0.122065), correlation (0.093285)*/,
-13,-8, -8,-9/*mean (0.162787), correlation (0.0942748)*/,
-11,7, -9,12/*mean (0.21561), correlation (0.0974438)*/,
7,7, 12,6/*mean (0.160583), correlation (0.130064)*/,
-4,-5, -3,0/*mean (0.228171), correlation (0.132998)*/,
-13,2, -12,-3/*mean (0.00997526), correlation (0.145926)*/,
-9,0, -7,5/*mean (0.198234), correlation (0.143636)*/,
12,-6, 12,-1/*mean (0.0676226), correlation (0.16689)*/,
-3,6, -2,12/*mean (0.166847), correlation (0.171682)*/,
-6,-13, -4,-8/*mean (0.101215), correlation (0.179716)*/,
11,-13, 12,-8/*mean (0.200641), correlation (0.192279)*/,
4,7, 5,1/*mean (0.205106), correlation (0.186848)*/,
5,-3, 10,-3/*mean (0.234908), correlation (0.192319)*/,
3,-7, 6,12/*mean (0.0709964), correlation (0.210872)*/,
-8,-7, -6,-2/*mean (0.0939834), correlation (0.212589)*/,
-2,11, -1,-10/*mean (0.127778), correlation (0.20866)*/,
-13,12, -8,10/*mean (0.14783), correlation (0.206356)*/,
-7,3, -5,-3/*mean (0.182141), correlation (0.198942)*/,
-4,2, -3,7/*mean (0.188237), correlation (0.21384)*/,
-10,-12, -6,11/*mean (0.14865), correlation (0.23571)*/,
5,-12, 6,-7/*mean (0.222312), correlation (0.23324)*/,
5,-6, 7,-1/*mean (0.229082), correlation (0.23389)*/,
1,0, 4,-5/*mean (0.241577), correlation (0.215286)*/,
9,11, 11,-13/*mean (0.00338507), correlation (0.251373)*/,
4,7, 4,12/*mean (0.131005), correlation (0.257622)*/,
2,-1, 4,4/*mean (0.152755), correlation (0.255205)*/,
-4,-12, -2,7/*mean (0.182771), correlation (0.244867)*/,
-8,-5, -7,-10/*mean (0.186898), correlation (0.23901)*/,
4,11, 9,12/*mean (0.226226), correlation (0.258255)*/,
0,-8, 1,-13/*mean (0.0897886), correlation (0.274827)*/,
-13,-2, -8,2/*mean (0.148774), correlation (0.28065)*/,
-3,-2, -2,3/*mean (0.153048), correlation (0.283063)*/,
-6,9, -4,-9/*mean (0.169523), correlation (0.278248)*/,
8,12, 10,7/*mean (0.225337), correlation (0.282851)*/,
0,9, 1,3/*mean (0.226687), correlation (0.278734)*/,
7,-5, 11,-10/*mean (0.00693882), correlation (0.305161)*/,
-13,-6, -11,0/*mean (0.0227283), correlation (0.300181)*/,
10,7, 12,1/*mean (0.125517), correlation (0.31089)*/,
-6,-3, -6,12/*mean (0.131748), correlation (0.312779)*/,
10,-9, 12,-4/*mean (0.144827), correlation (0.292797)*/,
-13,8, -8,-12/*mean (0.149202), correlation (0.308918)*/,
-13,0, -8,-4/*mean (0.160909), correlation (0.310013)*/,
3,3, 7,8/*mean (0.177755), correlation (0.309394)*/,
5,7, 10,-7/*mean (0.212337), correlation (0.310315)*/,
-1,7, 1,-12/*mean (0.214429), correlation (0.311933)*/,
3,-10, 5,6/*mean (0.235807), correlation (0.313104)*/,
2,-4, 3,-10/*mean (0.00494827), correlation (0.344948)*/,
-13,0, -13,5/*mean (0.0549145), correlation (0.344675)*/,
-13,-7, -12,12/*mean (0.103385), correlation (0.342715)*/,
-13,3, -11,8/*mean (0.134222), correlation (0.322922)*/,
-7,12, -4,7/*mean (0.153284), correlation (0.337061)*/,
6,-10, 12,8/*mean (0.154881), correlation (0.329257)*/,
-9,-1, -7,-6/*mean (0.200967), correlation (0.33312)*/,
-2,-5, 0,12/*mean (0.201518), correlation (0.340635)*/,
-12,5, -7,5/*mean (0.207805), correlation (0.335631)*/,
3,-10, 8,-13/*mean (0.224438), correlation (0.34504)*/,
-7,-7, -4,5/*mean (0.239361), correlation (0.338053)*/,
-3,-2, -1,-7/*mean (0.240744), correlation (0.344322)*/,
2,9, 5,-11/*mean (0.242949), correlation (0.34145)*/,
-11,-13, -5,-13/*mean (0.244028), correlation (0.336861)*/,
-1,6, 0,-1/*mean (0.247571), correlation (0.343684)*/,
5,-3, 5,2/*mean (0.000697256), correlation (0.357265)*/,
-4,-13, -4,12/*mean (0.00213675), correlation (0.373827)*/,
-9,-6, -9,6/*mean (0.0126856), correlation (0.373938)*/,
-12,-10, -8,-4/*mean (0.0152497), correlation (0.364237)*/,
10,2, 12,-3/*mean (0.0299933), correlation (0.345292)*/,
7,12, 12,12/*mean (0.0307242), correlation (0.366299)*/,
-7,-13, -6,5/*mean (0.0534975), correlation (0.368357)*/,
-4,9, -3,4/*mean (0.099865), correlation (0.372276)*/,
7,-1, 12,2/*mean (0.117083), correlation (0.364529)*/,
-7,6, -5,1/*mean (0.126125), correlation (0.369606)*/,
-13,11, -12,5/*mean (0.130364), correlation (0.358502)*/,
-3,7, -2,-6/*mean (0.131691), correlation (0.375531)*/,
7,-8, 12,-7/*mean (0.160166), correlation (0.379508)*/,
-13,-7, -11,-12/*mean (0.167848), correlation (0.353343)*/,
1,-3, 12,12/*mean (0.183378), correlation (0.371916)*/,
2,-6, 3,0/*mean (0.228711), correlation (0.371761)*/,
-4,3, -2,-13/*mean (0.247211), correlation (0.364063)*/,
-1,-13, 1,9/*mean (0.249325), correlation (0.378139)*/,
7,1, 8,-6/*mean (0.000652272), correlation (0.411682)*/,
1,-1, 3,12/*mean (0.00248538), correlation (0.392988)*/,
9,1, 12,6/*mean (0.0206815), correlation (0.386106)*/,
-1,-9, -1,3/*mean (0.0364485), correlation (0.410752)*/,
-13,-13, -10,5/*mean (0.0376068), correlation (0.398374)*/,
7,7, 10,12/*mean (0.0424202), correlation (0.405663)*/,
12,-5, 12,9/*mean (0.0942645), correlation (0.410422)*/,
6,3, 7,11/*mean (0.1074), correlation (0.413224)*/,
5,-13, 6,10/*mean (0.109256), correlation (0.408646)*/,
2,-12, 2,3/*mean (0.131691), correlation (0.416076)*/,
3,8, 4,-6/*mean (0.165081), correlation (0.417569)*/,
2,6, 12,-13/*mean (0.171874), correlation (0.408471)*/,
9,-12, 10,3/*mean (0.175146), correlation (0.41296)*/,
-8,4, -7,9/*mean (0.183682), correlation (0.402956)*/,
-11,12, -4,-6/*mean (0.184672), correlation (0.416125)*/,
1,12, 2,-8/*mean (0.191487), correlation (0.386696)*/,
6,-9, 7,-4/*mean (0.192668), correlation (0.394771)*/,
2,3, 3,-2/*mean (0.200157), correlation (0.408303)*/,
6,3, 11,0/*mean (0.204588), correlation (0.411762)*/,
3,-3, 8,-8/*mean (0.205904), correlation (0.416294)*/,
7,8, 9,3/*mean (0.213237), correlation (0.409306)*/,
-11,-5, -6,-4/*mean (0.243444), correlation (0.395069)*/,
-10,11, -5,10/*mean (0.247672), correlation (0.413392)*/,
-5,-8, -3,12/*mean (0.24774), correlation (0.411416)*/,
-10,5, -9,0/*mean (0.00213675), correlation (0.454003)*/,
8,-1, 12,-6/*mean (0.0293635), correlation (0.455368)*/,
4,-6, 6,-11/*mean (0.0404971), correlation (0.457393)*/,
-10,12, -8,7/*mean (0.0481107), correlation (0.448364)*/,
4,-2, 6,7/*mean (0.050641), correlation (0.455019)*/,
-2,0, -2,12/*mean (0.0525978), correlation (0.44338)*/,
-5,-8, -5,2/*mean (0.0629667), correlation (0.457096)*/,
7,-6, 10,12/*mean (0.0653846), correlation (0.445623)*/,
-9,-13, -8,-8/*mean (0.0858749), correlation (0.449789)*/,
-5,-13, -5,-2/*mean (0.122402), correlation (0.450201)*/,
8,-8, 9,-13/*mean (0.125416), correlation (0.453224)*/,
-9,-11, -9,0/*mean (0.130128), correlation (0.458724)*/,
1,-8, 1,-2/*mean (0.132467), correlation (0.440133)*/,
7,-4, 9,1/*mean (0.132692), correlation (0.454)*/,
-2,1, -1,-4/*mean (0.135695), correlation (0.455739)*/,
11,-6, 12,-11/*mean (0.142904), correlation (0.446114)*/,
-12,-9, -6,4/*mean (0.146165), correlation (0.451473)*/,
3,7, 7,12/*mean (0.147627), correlation (0.456643)*/,
5,5, 10,8/*mean (0.152901), correlation (0.455036)*/,
0,-4, 2,8/*mean (0.167083), correlation (0.459315)*/,
-9,12, -5,-13/*mean (0.173234), correlation (0.454706)*/,
0,7, 2,12/*mean (0.18312), correlation (0.433855)*/,
-1,2, 1,7/*mean (0.185504), correlation (0.443838)*/,
5,11, 7,-9/*mean (0.185706), correlation (0.451123)*/,
3,5, 6,-8/*mean (0.188968), correlation (0.455808)*/,
-13,-4, -8,9/*mean (0.191667), correlation (0.459128)*/,
-5,9, -3,-3/*mean (0.193196), correlation (0.458364)*/,
-4,-7, -3,-12/*mean (0.196536), correlation (0.455782)*/,
6,5, 8,0/*mean (0.1972), correlation (0.450481)*/,
-7,6, -6,12/*mean (0.199438), correlation (0.458156)*/,
-13,6, -5,-2/*mean (0.211224), correlation (0.449548)*/,
1,-10, 3,10/*mean (0.211718), correlation (0.440606)*/,
4,1, 8,-4/*mean (0.213034), correlation (0.443177)*/,
-2,-2, 2,-13/*mean (0.234334), correlation (0.455304)*/,
2,-12, 12,12/*mean (0.235684), correlation (0.443436)*/,
-2,-13, 0,-6/*mean (0.237674), correlation (0.452525)*/,
4,1, 9,3/*mean (0.23962), correlation (0.444824)*/,
-6,-10, -3,-5/*mean (0.248459), correlation (0.439621)*/,
-3,-13, -1,1/*mean (0.249505), correlation (0.456666)*/,
7,5, 12,-11/*mean (0.00119208), correlation (0.495466)*/,
4,-2, 5,-7/*mean (0.00372245), correlation (0.484214)*/,
-13,9, -9,-5/*mean (0.00741116), correlation (0.499854)*/,
7,1, 8,6/*mean (0.0208952), correlation (0.499773)*/,
7,-8, 7,6/*mean (0.0220085), correlation (0.501609)*/,
-7,-4, -7,1/*mean (0.0233806), correlation (0.496568)*/,
-8,11, -7,-8/*mean (0.0236505), correlation (0.489719)*/,
-13,6, -12,-8/*mean (0.0268781), correlation (0.503487)*/,
2,4, 3,9/*mean (0.0323324), correlation (0.501938)*/,
10,-5, 12,3/*mean (0.0399235), correlation (0.494029)*/,
-6,-5, -6,7/*mean (0.0420153), correlation (0.486579)*/,
8,-3, 9,-8/*mean (0.0548021), correlation (0.484237)*/,
2,-12, 2,8/*mean (0.0616622), correlation (0.496642)*/,
-11,-2, -10,3/*mean (0.0627755), correlation (0.498563)*/,
-12,-13, -7,-9/*mean (0.0829622), correlation (0.495491)*/,
-11,0, -10,-5/*mean (0.0843342), correlation (0.487146)*/,
5,-3, 11,8/*mean (0.0929937), correlation (0.502315)*/,
-2,-13, -1,12/*mean (0.113327), correlation (0.48941)*/,
-1,-8, 0,9/*mean (0.132119), correlation (0.467268)*/,
-13,-11, -12,-5/*mean (0.136269), correlation (0.498771)*/,
-10,-2, -10,11/*mean (0.142173), correlation (0.498714)*/,
-3,9, -2,-13/*mean (0.144141), correlation (0.491973)*/,
2,-3, 3,2/*mean (0.14892), correlation (0.500782)*/,
-9,-13, -4,0/*mean (0.150371), correlation (0.498211)*/,
-4,6, -3,-10/*mean (0.152159), correlation (0.495547)*/,
-4,12, -2,-7/*mean (0.156152), correlation (0.496925)*/,
-6,-11, -4,9/*mean (0.15749), correlation (0.499222)*/,
6,-3, 6,11/*mean (0.159211), correlation (0.503821)*/,
-13,11, -5,5/*mean (0.162427), correlation (0.501907)*/,
11,11, 12,6/*mean (0.16652), correlation (0.497632)*/,
7,-5, 12,-2/*mean (0.169141), correlation (0.484474)*/,
-1,12, 0,7/*mean (0.169456), correlation (0.495339)*/,
-4,-8, -3,-2/*mean (0.171457), correlation (0.487251)*/,
-7,1, -6,7/*mean (0.175), correlation (0.500024)*/,
-13,-12, -8,-13/*mean (0.175866), correlation (0.497523)*/,
-7,-2, -6,-8/*mean (0.178273), correlation (0.501854)*/,
-8,5, -6,-9/*mean (0.181107), correlation (0.494888)*/,
-5,-1, -4,5/*mean (0.190227), correlation (0.482557)*/,
-13,7, -8,10/*mean (0.196739), correlation (0.496503)*/,
1,5, 5,-13/*mean (0.19973), correlation (0.499759)*/,
1,0, 10,-13/*mean (0.204465), correlation (0.49873)*/,
9,12, 10,-1/*mean (0.209334), correlation (0.49063)*/,
5,-8, 10,-9/*mean (0.211134), correlation (0.503011)*/,
-1,11, 1,-13/*mean (0.212), correlation (0.499414)*/,
-9,-3, -6,2/*mean (0.212168), correlation (0.480739)*/,
-1,-10, 1,12/*mean (0.212731), correlation (0.502523)*/,
-13,1, -8,-10/*mean (0.21327), correlation (0.489786)*/,
8,-11, 10,-6/*mean (0.214159), correlation (0.488246)*/,
2,-13, 3,-6/*mean (0.216993), correlation (0.50287)*/,
7,-13, 12,-9/*mean (0.223639), correlation (0.470502)*/,
-10,-10, -5,-7/*mean (0.224089), correlation (0.500852)*/,
-10,-8, -8,-13/*mean (0.228666), correlation (0.502629)*/,
4,-6, 8,5/*mean (0.22906), correlation (0.498305)*/,
3,12, 8,-13/*mean (0.233378), correlation (0.503825)*/,
-4,2, -3,-3/*mean (0.234323), correlation (0.476692)*/,
5,-13, 10,-12/*mean (0.236392), correlation (0.475462)*/,
4,-13, 5,-1/*mean (0.236842), correlation (0.504132)*/,
-9,9, -4,3/*mean (0.236977), correlation (0.497739)*/,
0,3, 3,-9/*mean (0.24314), correlation (0.499398)*/,
-12,1, -6,1/*mean (0.243297), correlation (0.489447)*/,
3,2, 4,-8/*mean (0.00155196), correlation (0.553496)*/,
-10,-10, -10,9/*mean (0.00239541), correlation (0.54297)*/,
8,-13, 12,12/*mean (0.0034413), correlation (0.544361)*/,
-8,-12, -6,-5/*mean (0.003565), correlation (0.551225)*/,
2,2, 3,7/*mean (0.00835583), correlation (0.55285)*/,
10,6, 11,-8/*mean (0.00885065), correlation (0.540913)*/,
6,8, 8,-12/*mean (0.0101552), correlation (0.551085)*/,
-7,10, -6,5/*mean (0.0102227), correlation (0.533635)*/,
-3,-9, -3,9/*mean (0.0110211), correlation (0.543121)*/,
-1,-13, -1,5/*mean (0.0113473), correlation (0.550173)*/,
-3,-7, -3,4/*mean (0.0140913), correlation (0.554774)*/,
-8,-2, -8,3/*mean (0.017049), correlation (0.55461)*/,
4,2, 12,12/*mean (0.01778), correlation (0.546921)*/,
2,-5, 3,11/*mean (0.0224022), correlation (0.549667)*/,
6,-9, 11,-13/*mean (0.029161), correlation (0.546295)*/,
3,-1, 7,12/*mean (0.0303081), correlation (0.548599)*/,
11,-1, 12,4/*mean (0.0355151), correlation (0.523943)*/,
-3,0, -3,6/*mean (0.0417904), correlation (0.543395)*/,
4,-11, 4,12/*mean (0.0487292), correlation (0.542818)*/,
2,-4, 2,1/*mean (0.0575124), correlation (0.554888)*/,
-10,-6, -8,1/*mean (0.0594242), correlation (0.544026)*/,
-13,7, -11,1/*mean (0.0597391), correlation (0.550524)*/,
-13,12, -11,-13/*mean (0.0608974), correlation (0.55383)*/,
6,0, 11,-13/*mean (0.065126), correlation (0.552006)*/,
0,-1, 1,4/*mean (0.074224), correlation (0.546372)*/,
-13,3, -9,-2/*mean (0.0808592), correlation (0.554875)*/,
-9,8, -6,-3/*mean (0.0883378), correlation (0.551178)*/,
-13,-6, -8,-2/*mean (0.0901035), correlation (0.548446)*/,
5,-9, 8,10/*mean (0.0949843), correlation (0.554694)*/,
2,7, 3,-9/*mean (0.0994152), correlation (0.550979)*/,
-1,-6, -1,-1/*mean (0.10045), correlation (0.552714)*/,
9,5, 11,-2/*mean (0.100686), correlation (0.552594)*/,
11,-3, 12,-8/*mean (0.101091), correlation (0.532394)*/,
3,0, 3,5/*mean (0.101147), correlation (0.525576)*/,
-1,4, 0,10/*mean (0.105263), correlation (0.531498)*/,
3,-6, 4,5/*mean (0.110785), correlation (0.540491)*/,
-13,0, -10,5/*mean (0.112798), correlation (0.536582)*/,
5,8, 12,11/*mean (0.114181), correlation (0.555793)*/,
8,9, 9,-6/*mean (0.117431), correlation (0.553763)*/,
7,-4, 8,-12/*mean (0.118522), correlation (0.553452)*/,
-10,4, -10,9/*mean (0.12094), correlation (0.554785)*/,
7,3, 12,4/*mean (0.122582), correlation (0.555825)*/,
9,-7, 10,-2/*mean (0.124978), correlation (0.549846)*/,
7,0, 12,-2/*mean (0.127002), correlation (0.537452)*/,
-1,-6, 0,-11/*mean (0.127148), correlation (0.547401)*/
};
/**
* @brief 计算ORB特征点的描述子。注意这个是全局的静态函数,只能是在本文件内被调用
* @param[in] kpt 特征点对象
* @param[in] img 提取出特征点的图像
* @param[in] pattern 预定义好的随机采样点集
* @param[out] desc 用作输出变量,保存计算好的描述子,长度为32*8bit
*/
static void computeOrbDescriptor(const KeyPoint& kpt,
const Mat& img, const Point* pattern,
uchar* desc)
{
//得到特征点的角度,用弧度制表示。kpt.angle是角度制,范围为[0,360)度
float angle = (float)kpt.angle*factorPI;
//然后计算这个角度的余弦值和正弦值
float a = (float)cos(angle), b = (float)sin(angle);
//获得图像中心指针
const uchar* center = &img.at
(cvRound(kpt.pt.y), cvRound(kpt.pt.x));
//获得图像的每行的字节数
const int step = (int)img.step;
//原始的BRIEF描述子不具有方向信息,通过加入特征点的方向来计算描述子,称之为Steer BRIEF,具有较好旋转不变特性
//具体地,在计算的时候需要将这里选取的随机点点集的x轴方向旋转到特征点的方向。
//获得随机“相对点集”中某个idx所对应的点的灰度,这里旋转前坐标为(x,y), 旋转后坐标(x',y')推导:
// x'= xcos(θ) - ysin(θ), y'= xsin(θ) + ycos(θ)
// 获取对应位置的想数值
#define GET_VALUE(idx) \
center[cvRound(pattern[idx].x*b + pattern[idx].y*a)*step + \
cvRound(pattern[idx].x*a - pattern[idx].y*b)]
//brief描述子由32*8位组成
//其中每一位是来自于两个像素点灰度的直接比较,所以每比较出8bit结果,需要16个随机点,这也就是为什么pattern需要+=16的原因
for (int i = 0; i < 32; ++i, pattern += 16)
{
int t0, //参与比较的一个特征点的灰度值
t1, //参与比较的另一个特征点的灰度值
val; //描述子这个字节的比较结果
t0 = GET_VALUE(0); t1 = GET_VALUE(1);
val = t0 < t1; //描述子本字节的bit0
t0 = GET_VALUE(2); t1 = GET_VALUE(3);
val |= (t0 < t1) << 1; //描述子本字节的bit1
t0 = GET_VALUE(4); t1 = GET_VALUE(5);
val |= (t0 < t1) << 2; //描述子本字节的bit2
t0 = GET_VALUE(6); t1 = GET_VALUE(7);
val |= (t0 < t1) << 3; //描述子本字节的bit3
t0 = GET_VALUE(8); t1 = GET_VALUE(9);
val |= (t0 < t1) << 4; //描述子本字节的bit4
t0 = GET_VALUE(10); t1 = GET_VALUE(11);
val |= (t0 < t1) << 5; //描述子本字节的bit5
t0 = GET_VALUE(12); t1 = GET_VALUE(13);
val |= (t0 < t1) << 6; //描述子本字节的bit6
t0 = GET_VALUE(14); t1 = GET_VALUE(15);
val |= (t0 < t1) << 7; //描述子本字节的bit7
desc[i] = (uchar)val; //保存当前比较的出来的描述子的这个字节
}
#undef GET_VALUE
}
1.3 ORB 特征
==(即FAST关键点和加了旋转不变性的BRIEF 描述子)==
原始的FAST关键点没有方向信息,这样当图像发生旋转后,brief描述子也会发生变化,使得特征点对旋
转不鲁棒.
解决办法:使用灰度质心法计算特征点的方向。在一个圆内计算灰度质心
下图P为几何中心,Q为灰度质心

计算公式如下:
R是以几何中心为圆心的圆的半径
$I(x,y)$是对应$(x,y)$的像素值
后面的公式就是高中物理里面质心的计算公式,只不过密度变成了像素值
/**
* @brief 这个函数用于计算特征点的方向,这里是返回角度作为方向。
* 计算特征点方向是为了使得提取的特征点具有旋转不变性。
* 方法是灰度质心法:以几何中心和灰度质心的连线作为该特征点方向
* @param[in] image 要进行操作的某层金字塔图像
* @param[in] pt 当前特征点的坐标
* @param[in] u_max 图像块的每一行的坐标边界 u_max
* @return float 返回特征点的角度,范围为[0,360)角度,精度为0.3°
*/
static float IC_Angle(const Mat& image, Point2f pt, const vector
& u_max)
{
//图像的矩,前者是按照图像块的y坐标加权,后者是按照图像块的x坐标加权
int m_01 = 0, m_10 = 0;
//获得这个特征点所在的图像块的中心点坐标灰度值的指针center
const uchar* center = &image.at
(cvRound(pt.y), cvRound(pt.x));
// Treat the center line differently, v=0
//这条v=0中心线的计算需要特殊对待
//后面是以中心行为对称轴,成对遍历行数,所以PATCH_SIZE必须是奇数
for (int u = -HALF_PATCH_SIZE; u <= HALF_PATCH_SIZE; ++u)
m_10 += u * center[u]; //注意这里的center下标u可以是负的!中心水平线上的像素按x坐标(也就是u坐标)加权
// Go line by line in the circuI853lar patch
int step = (int)image.step1(); //这里的step1表示这个图像一行包含的字节总数。参考[https://blog.csdn.net/qianqing13579/article/details/45318279]
for (int v = 1; v <= HALF_PATCH_SIZE; ++v) // 行
{
// Proceed over the two lines
//本来m_01应该是一列一列地计算的,但是由于对称以及坐标x,y正负的原因,可以一次计算两行
int v_sum = 0; // 列的和,即y坐标加权和
int d = u_max[v]; // 获取某行像素横坐标的最大范围,注意这里的图像块是圆形的!
//在坐标范围内挨个像素遍历,实际是一次遍历2个
// 假设每次处理的两个点坐标,中心线下方为(x,y),中心线上方为(x,-y)
// 对于某次待处理的两个点:m_10 = Σ x*I(x,y) = x*I(x,y) + x*I(x,-y) = x*(I(x,y) + I(x,-y))
// 对于某次待处理的两个点:m_01 = Σ y*I(x,y) = y*I(x,y) - y*I(x,-y) = y*(I(x,y) - I(x,-y))
for (int u = -d; u <= d; ++u) // 列
{
//得到需要进行加运算和减运算的像素灰度值
//val_plus:在中心线下方x=u,y=v时的的像素灰度值
//val_minus:在中心线上方x=u,y=-v时的像素灰度值
int val_plus = center[u + v*step], val_minus = center[u - v*step];
v_sum += (val_plus - val_minus);//在v(y轴)上,2行所有像素灰度值之差
//u轴(也就是x轴)方向上用u坐标加权和(u坐标也有正负符号),相当于同时计算两行
m_10 += u * (val_plus + val_minus);
}
m_01 += v * v_sum;
}
return fastAtan2((float)m_01, (float)m_10);
}
1.4 半径R的圆的坐标范围
如图所示,因为像素坐标是离散的,所以为了得到一个比较平滑的圆。ORB里面计算了1/4个圆的边界。并通过对称关系得到整个圆
== 思想:==
当0<v<vmax时,我们通过三角形AGH,利用勾股定理计算umax[v]。 当v>vmax,我们就利用圆的对称性,计算余下的umax[v]。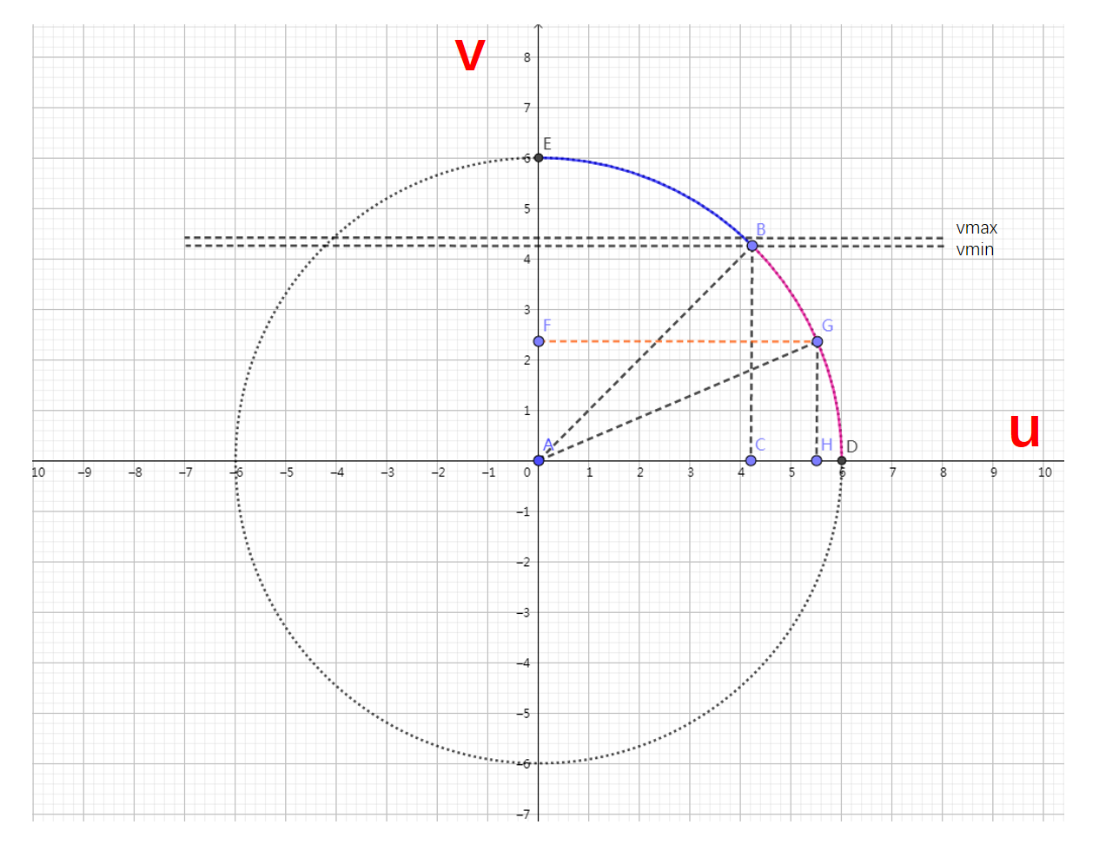
//This is for orientation
//下面的内容是和特征点的旋转计算有关的
// pre-compute the end of a row in a circular patch
//预先计算圆形patch中行的结束位置
//+1中的1表示那个圆的中间行
umax.resize(HALF_PATCH_SIZE + 1);
//cvFloor返回不大于参数的最大整数值,cvCeil返回不小于参数的最小整数值,cvRound则是四舍五入
int v, //循环辅助变量
v0, //辅助变量
vmax = cvFloor(HALF_PATCH_SIZE * sqrt(2.f) / 2 + 1); //计算圆的最大行号,+1应该是把中间行也给考虑进去了
//NOTICE 注意这里的最大行号指的是计算的时候的最大行号,此行的和圆的角点在45°圆心角的一边上,之所以这样选择
//是因为圆周上的对称特性 vmax=11
//这里的二分之根2就是对应那个45°圆心角
int vmin = cvCeil(HALF_PATCH_SIZE * sqrt(2.f) / 2); //vmin=11
//半径的平方
const double hp2 = HALF_PATCH_SIZE*HALF_PATCH_SIZE;
//利用圆的方程计算每行像素的u坐标边界(max)
for (v = 0; v <= vmax; ++v) // 这里计算的1/8个圆,45°
umax[v] = cvRound(sqrt(hp2 - v * v));//结果都是大于0的结果,表示x坐标在这一行的边界
// umax[11]=10
// Make sure we are symmetric
//这里其实是使用了对称的方式计算上四分之一的圆周上的umax,目的也是为了保持严格的对称(如果按照常规的想法做,由于cvRound就会很容易出现不对称的情况,
//同时这些随机采样的特征点集也不能够满足旋转之后的采样不变性了)
// 想象成前面的U, V互换就行了
for (v = HALF_PATCH_SIZE, v0 = 0; v >= vmin; --v)
{
// 因为圆上面的v变化小,这里找到umax相差至少一个像素的v0坐标,后面的就每个v0和v0 + 1的umax都不同了
while (umax[v0] == umax[v0 + 1])
++v0;
umax[v] = v0;
++v0;
}
二、图像金子塔
构建图像金子塔的目的:实现特征点的尺度不变性
一句话概括图像金字塔:就是对原图进行多次缩放,组成一组原图的不同分辨率的图像组std::vector
/**
* 构建图像金字塔
* @param image 输入原图像(gray),这个输入图像所有像素都是有效的,也就是说都是可以在其上提取出FAST角点的
*/
void ORBextractor::ComputePyramid(cv::Mat image)
{
for (int level = 0; level < nlevels; ++level)
{
float scale = mvInvScaleFactor[level];//获取本层图像的缩放系数
Size sz(cvRound((float)image.cols*scale), cvRound((float)image.rows*scale));//计算本层图像的像素尺寸大小
Size wholeSize(sz.width + EDGE_THRESHOLD*2, sz.height + EDGE_THRESHOLD*2);//为了对图像边沿也能高斯模糊,将图像进行“补边”,EDGE_THRESHOLD区域的图像不进行FAST角点检测
Mat temp(wholeSize, image.type()), masktemp;// 定义了两个变量:temp是扩展了边界的图像,masktemp并未使用
// mvImagePyramid 刚开始时是个空的vector
// 把图像金字塔该图层的图像指针mvImagePyramid指向temp的中间部分(这里为浅拷贝,内存相同)
// 这里相当于把中间没有增加边的原始的部分给抠出来了,只是为了预先指定每一层的大小
mvImagePyramid[level] = temp(Rect(EDGE_THRESHOLD, EDGE_THRESHOLD, sz.width, sz.height));
// Compute the resized image
//计算第0层以上resize后的图像
if( level != 0 )
{
//将上一层金字塔图像根据设定sz缩放到当前层级
resize(mvImagePyramid[level-1], //输入图像
mvImagePyramid[level], //输出图像
sz, //输出图像的尺寸(没有边)
0, //水平方向上的缩放系数,留0表示自动计算
0, //垂直方向上的缩放系数,留0表示自动计算
cv::INTER_LINEAR); //图像缩放的差值算法类型,这里的是线性插值算法
//把源图像拷贝到目的图像的中央,四面填充指定的像素。
//为了对边界也进行高斯模糊需要没给原图增加一个边界
//EDGE_THRESHOLD指的这个边界的宽度,由于这个边界之外的像素不是原图像素而是算法生成出来的,所以不能够在EDGE_THRESHOLD之外提取特征点
copyMakeBorder(mvImagePyramid[level], //源图像
temp, //目标图像(此时其实就已经有大了一圈的尺寸了)
EDGE_THRESHOLD, EDGE_THRESHOLD, //top & bottom 需要扩展的border大小
EDGE_THRESHOLD, EDGE_THRESHOLD, //left & right 需要扩展的border大小
BORDER_REFLECT_101+BORDER_ISOLATED); //扩充方式,opencv给出的解释:
}
else
{
//对于底层图像,直接就扩充边界了
copyMakeBorder(image, //这里是原图像
temp, EDGE_THRESHOLD, EDGE_THRESHOLD, EDGE_THRESHOLD, EDGE_THRESHOLD,
BORDER_REFLECT_101);
}
}
}
图像金字塔详细:https://www.cnblogs.com/long5683/p/9671005.html
因为ORB_SLAM每一个Frame的特征点数目是固定的,所以需要通过图像金字塔的尺寸分配每一层的特征点数目:
参考:https://zhuanlan.zhihu.com/p/61738607
float factor = 1.0f / scaleFactor; //图片降采样缩放系数的倒数
//第0层所希望的特征点个数 a1=Sn*(1-q)/(1-q^n)
float nDesiredFeaturesPerScale = nfeatures*(1 - factor)/(1 - (float)pow((double)factor, (double)nlevels));
//用于计算最后一层的特征点个数,前几层特征点的累计计数
int sumFeatures = 0;
//开始逐层计算要分配的特征点个数,顶层图像除外(看循环后面)
for( int level = 0; level < nlevels-1; level++ )
{
//分配 cvRound : 返回个参数最接近的整数值
mnFeaturesPerLevel[level] = cvRound(nDesiredFeaturesPerScale);
//累计特征点数
sumFeatures += mnFeaturesPerLevel[level];
//乘系数=第level层的特征点数目
nDesiredFeaturesPerScale *= factor;
}
//由于前面的特征点个数取整操作,可能会导致剩余一些特征点个数没有被分配,所以这里就将这个余出来的特征点分配到最高的图层中
mnFeaturesPerLevel[nlevels-1] = std::max(nfeatures - sumFeatures, 0);
三、四叉树均匀分布特征点
三维叫八叉树,图像是二维的所以叫四叉树
==算法步骤:==
(1)根节点=w/h个。一般的640×480的图像开始的时候只有一个根node。
(2)如果node里面的点数>1,把每个node分成四个node,如果node里面的特征点为空,就删掉这个node。
(3)新分的node的点数>1,就再分裂成4个node。如此,一直分裂。终止条件为:node的总数量> 需求的数量 ,或者无法再进行分裂。
(4)然后从每个node里面选择一个质量最好的FAST点。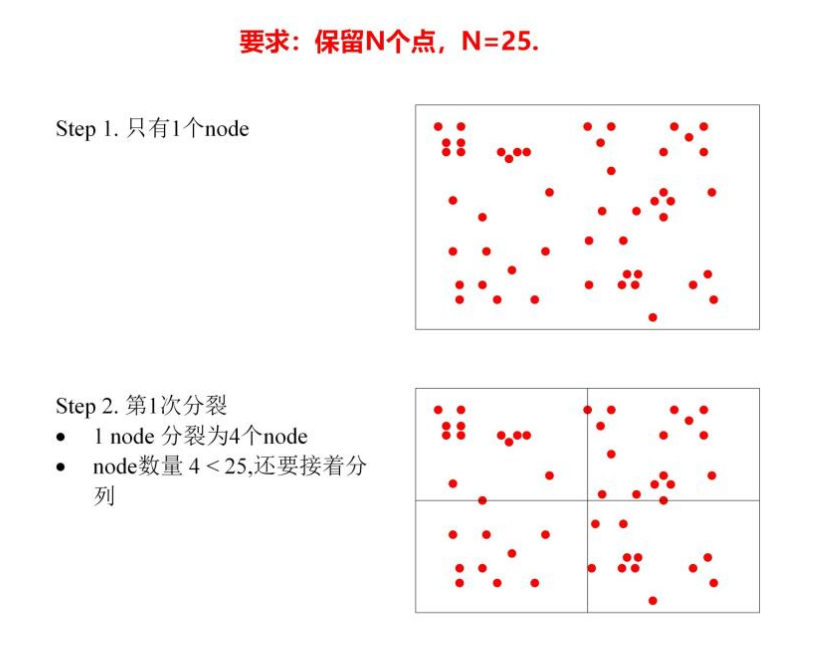
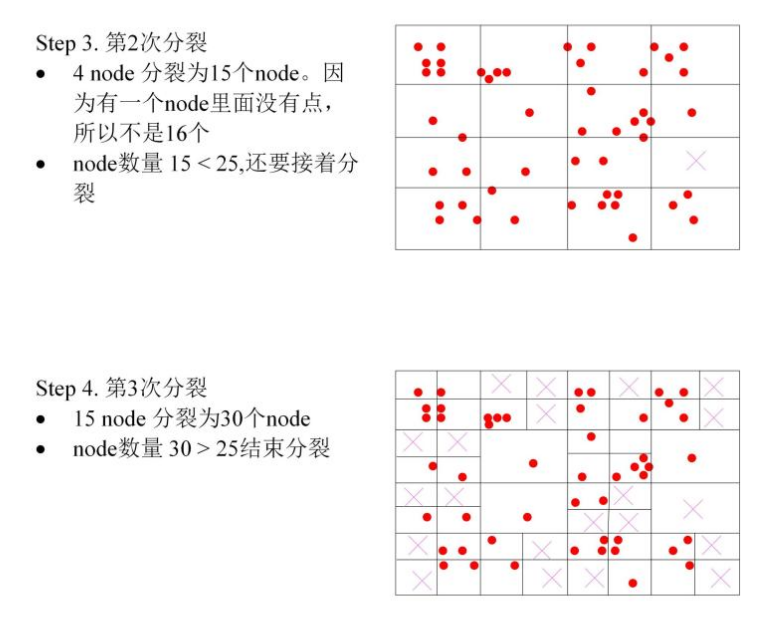
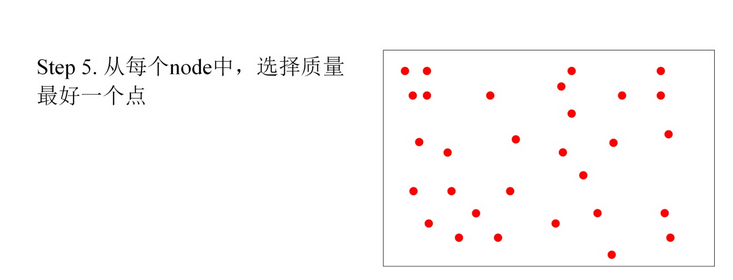
参考:https://zhuanlan.zhihu.com/p/61738607
/**
* @brief 使用四叉树法对一个图像金字塔图层中的特征点进行平均和分发
* 注意到这个函数应该是直接使用成员函数,图像金字塔中的图像,因为并没出现任何图像的函数参数
* @param[in] vToDistributeKeys 等待进行分配到四叉树中的特征点(在特征提取坐标下,即边=3)
* @param[in] minX 当前图层的图像的边界=EDGE_THRESHOLD-3;
* @param[in] maxX
* @param[in] minY
* @param[in] maxY
* @param[in] N 希望提取出的特征点个数
* @param[in] level 指定的金字塔图层,并未使用
* @return vector
已经均匀分散好的特征点vector容器
*/
vector
ORBextractor::DistributeOctTree(const vector
& vToDistributeKeys, const int &minX,
const int &maxX, const int &minY, const int &maxY, const int &N, const int &level)
{
// Compute how many initial nodes、
// Step 1 根据宽高比确定初始节点数目
//计算应该生成的初始节点个数,根节点的数量nIni是根据边界的宽高比值确定的,一般是1或者2
/** @note 这里nIni虽然算的是宽高比,但实际意义是初始节点个数,千万别当成宽高比*/
// ! bug: 如果宽高比小于0.5,nIni=0, 后面hx会报错
const int nIni = round(static_cast
(maxX-minX)/(maxY-minY));
//一个初始的节点的x方向有多少个像素
const float hX = static_cast
(maxX-minX)/nIni; //存储有提取器节点的列表 // ExtractorNode中UL、UR、BL、BR记录了该节点(区域)的四个顶点坐标 // ExtractorNode中的vKeys记录了属于该节点(区域)的所有特征点,这里有些低效,容器里存的是特征点而不是特征点的指针 list
lNodes; //存储初始提取器节点指针的vector // 记录初始节点的指针,为了方便根据特征点x坐标快速找到对应的节点(x/hX) vector<ExtractorNode*> vpIniNodes; //然后重新设置其大小 vpIniNodes.resize(nIni); // step1: 建立分裂的初始节点 // step1.1:确定节点区域 for(int i=0; i<nIni; i++) { //生成一个提取器节点 ExtractorNode ni; //设置提取器节点的图像边界 //注意这里和提取FAST角点区域相同,特征点坐标从0 开始 ni.UL = cv::Point2i(hX*static_cast
(i),0); // 左上 ni.UR = cv::Point2i(hX*static_cast
(i+1),0); // 右上 //NOTICE 注意这里是直接到了图像的底部,也就是说,按照作者的意思,应该是图像的width>height? ni.BL = cv::Point2i(ni.UL.x,maxY-minY); // 左下 ni.BR = cv::Point2i(ni.UR.x,maxY-minY); // 右下 //重设vkeys大小 ni.vKeys.reserve(vToDistributeKeys.size()); //将刚才生成的提取节点添加到列表中 //虽然这里的ni是局部变量,但是由于这里的push_back()是拷贝参数的内容到一个新的对象中然后再添加到列表中 //所以当本函数退出之后这里的内存不会成为“野指针” lNodes.push_back(ni); //存储这个初始的提取器节点句柄 vpIniNodes[i] = &lNodes.back(); } //Associate points to childs // Step 3 将特征点分配到子提取器节点中(区域) for(size_t i=0;i<vToDistributeKeys.size();i++) { //获取这个特征点对象 const cv::KeyPoint &kp = vToDistributeKeys[i]; //按特征点的横轴位置,分配给属于那个图像区域的提取器节点(最初的提取器节点) // NOTE 这里相当于把点赋值给了lNodes里面的根节点 vpIniNodes[kp.pt.x/hX]->vKeys.push_back(kp); } // Step 4 遍历此提取器节点列表,标记那些不可再分裂的节点,删除那些没有分配到特征点的节点 // ? 这个步骤是必要的吗?感觉可以省略,通过判断nIni个数和vKeys.size() 就可以吧 list
::iterator lit = lNodes.begin(); /* 判断根节点可否分裂*/ while(lit!=lNodes.end()) { //如果初始的提取器节点所分配到的特征点个数为1 if(lit->vKeys.size()==1) { //那么就标志位置位,表示此节点不可再分 lit->bNoMore=true; //更新迭代器 lit++; } ///如果一个提取器节点没有被分配到特征点,那么就从列表中直接删除它 else if(lit->vKeys.empty()) //注意,由于是直接删除了它,所以这里的迭代器没有必要更新;否则反而会造成跳过元素的情况 lit = lNodes.erase(lit); else//lit->vKeys.size() 节点的特征点>1 ,不做处理,迭代器++ lit++; } //结束标志位清空 bool bFinish = false; //记录迭代次数,只是记录,并未起到作用 int iteration = 0; //声明一个vector用于存储节点的vSize和句柄对 //这个变量记录了在一次分裂循环中,那些可以再继续进行分裂的节点中包含的特征点数目和其句柄 vector<pair<int,ExtractorNode*> > vSizeAndPointerToNode; //调整大小,这里的意思是一个初始化节点将“分裂”成为四个 vSizeAndPointerToNode.reserve(lNodes.size()*4); // Step 5 根据兴趣点分布,利用4叉树方法对图像进行划分区域 while(!bFinish) { //更新迭代次数计数器,只是记录,并未起到作用 iteration++; //保存当前节点个数,prev在这里理解为“保留”比较好 int prevSize = lNodes.size(); //重新定位迭代器指向列表头部 lit = lNodes.begin(); //需要展开的节点计数,这个一直保持累计,不清零 int nToExpand = 0; //因为是在循环中,前面的循环体中可能污染了这个变量,so清空这个vector //这个变量也只是统计了某一个循环中的点 //这个变量记录了在一次分裂循环中,那些可以再继续进行分裂的节点中包含的特征点数目和其句柄 vSizeAndPointerToNode.clear(); // 将目前的子区域进行划分 //开始遍历列表中所有的提取器节点,并进行分解或者保留 //分裂过的节点会被删除,只留下叶子节点 while(lit!=lNodes.end()) { //如果提取器节点只有一个特征点,不能分裂了 if(lit->bNoMore) { // If node only contains one point do not subdivide and continue //那么就没有必要再进行细分了 lit++; //跳过当前节点,继续下一个 continue; } else // 如果这个区域不止一个特征点,则进一步细分成四个子区域 { // If more than one point, subdivide ExtractorNode n1,n2,n3,n4; lit->DivideNode(n1,n2,n3,n4); // Add childs if they contain points //如果这里分出来的子区域中有特征点,那么就将这个子区域的节点添加到提取器节点的列表中 //注意这里的条件是,有特征点即可 if(n1.vKeys.size()>0) { // note:将新分裂出的节点插入到容器前面,迭代器后面的都是上一次分裂还未访问的节点 // 即越后面的点越靠近根节点,链表最后为根节点 lNodes.push_front(n1); //再判断其中子提取器节点中的特征点数目是否大于1 if(n1.vKeys.size()>1) { //如果有超过一个的特征点,那么“待展开的节点计数++” nToExpand++; //保存这个特征点数目和节点指针的信息 vSizeAndPointerToNode.push_back(make_pair(n1.vKeys.size(),&lNodes.front())); //?这个访问用的句柄貌似并没有用到? // lNodes.front().lit 和前面的迭代的lit 不同,只是名字相同而已 // lNodes.front().lit是node结构体里的一个指针用来记录节点的位置 // 迭代的lit 是while循环里作者命名的遍历的指针名称 lNodes.front().lit = lNodes.begin(); } } //后面的操作都是相同的,这里不再赘述 if(n2.vKeys.size()>0) { lNodes.push_front(n2); if(n2.vKeys.size()>1) { nToExpand++; vSizeAndPointerToNode.push_back(make_pair(n2.vKeys.size(),&lNodes.front())); lNodes.front().lit = lNodes.begin(); } } if(n3.vKeys.size()>0) { lNodes.push_front(n3); if(n3.vKeys.size()>1) { nToExpand++; vSizeAndPointerToNode.push_back(make_pair(n3.vKeys.size(),&lNodes.front())); lNodes.front().lit = lNodes.begin(); } } if(n4.vKeys.size()>0) { lNodes.push_front(n4); if(n4.vKeys.size()>1) { nToExpand++; vSizeAndPointerToNode.push_back(make_pair(n4.vKeys.size(),&lNodes.front())); lNodes.front().lit = lNodes.begin(); } } //当这个母节点expand之后就从列表中删除它了,能够进行分裂操作说明至少有一个子节点的区域中特征点的数量是>1的 //? 分裂方式是后加的先分裂,先加的后分裂。 lit=lNodes.erase(lit); //继续下一次循环,其实这里加不加这句话的作用都是一样的 continue; }//判断当前遍历到的节点中是否有超过一个的特征点 }//遍历列表中的所有提取器节点 // Finish if there are more nodes than required features or all nodes contain just one point //停止这个过程的条件有两个,满足其中一个即可: //1、当前的节点数已经超过了要求的特征点数 //2、当前所有的节点中都只包含一个特征点 if((int)lNodes.size()>=N //判断是否超过了要求的特征点数 || (int)lNodes.size()==prevSize) //prevSize中保存的是分裂之前的节点个数,如果分裂之前和分裂之后的总节点个数一样,说明当前所有的 //节点区域中只有一个特征点,已经不能够再细分了 { //停止标志置位 bFinish = true; } // Step 6 当再划分之后所有的Node数大于要求数目时,就慢慢划分直到使其刚刚达到或者超过要求的特征点个数 //可以展开的子节点个数nToExpand x3,是因为一分四之后,会删除原来的主节点,所以乘以3 /** * //?BUG 但是我觉得这里有BUG,虽然最终作者也给误打误撞、稀里糊涂地修复了 * 注意到,这里的nToExpand变量在前面的执行过程中是一直处于累计状态的,如果因为特征点个数太少,跳过了下面的else-if,又进行了一次上面的遍历 * list的操作之后,lNodes.size()增加了,但是nToExpand也增加了,尤其是在很多次操作之后,下面的表达式: * ((int)lNodes.size()+nToExpand*3)>N * 会很快就被满足,但是此时只进行一次对vSizeAndPointerToNode中点进行分裂的操作是肯定不够的; * 理想中,作者下面的for理论上只要执行一次就能满足,不过作者所考虑的“不理想情况”应该是分裂后出现的节点所在区域可能没有特征点,因此将for * 循环放在了一个while循环里面,通过再次进行for循环、再分裂一次解决这个问题。而我所考虑的“不理想情况”则是因为前面的一次对vSizeAndPointerToNode * 中的特征点进行for循环不够,需要将其放在另外一个循环(也就是作者所写的while循环)中不断尝试直到达到退出条件。 * */ else if(((int)lNodes.size()+nToExpand*3)>N) { //如果再分裂一次那么数目就要超了,这里想办法尽可能使其刚刚达到或者超过要求的特征点个数时就退出 //这里的nToExpand和vSizeAndPointerToNode不是一次循环对一次循环的关系,而是前者是累计计数,后者只保存某一个循环的 //一直循环,直到结束标志位被置位 while(!bFinish) { //获取当前的list中的节点个数 prevSize = lNodes.size(); //Prev这里是应该是保留的意思吧,保留那些还可以分裂的节点的信息, 这里是深拷贝 vector<pair<int,ExtractorNode*> > vPrevSizeAndPointerToNode = vSizeAndPointerToNode; //清空 vSizeAndPointerToNode.clear(); // 对需要划分的节点进行排序,对pair对的第一个元素进行排序,默认是从小到大排序 // 优先分裂特征点多的节点,使得特征点密集的区域保留更少的特征点 //! TODO 注意这里的排序规则非常重要!会导致每次最后产生的特征点都不一样。建议使用 stable_sort // https://blog.csdn.net/earbao/article/details/54911878 sort(vPrevSizeAndPointerToNode.begin(),vPrevSizeAndPointerToNode.end()); //遍历这个存储了pair对的vector,注意是从后往前遍历 for(int j=vPrevSizeAndPointerToNode.size()-1;j>=0;j--) { ExtractorNode n1,n2,n3,n4; //对每个需要进行分裂的节点进行分裂 vPrevSizeAndPointerToNode[j].second->DivideNode(n1,n2,n3,n4); // Add childs if they contain points //其实这里的节点可以说是二级子节点了,执行和前面一样的操作 if(n1.vKeys.size()>0) { lNodes.push_front(n1); if(n1.vKeys.size()>1) { //因为这里还有对于vSizeAndPointerToNode的操作,所以前面才会备份vSizeAndPointerToNode中的数据 //为可能的、后续的又一次for循环做准备 vSizeAndPointerToNode.push_back(make_pair(n1.vKeys.size(),&lNodes.front())); lNodes.front().lit = lNodes.begin(); } } if(n2.vKeys.size()>0) { lNodes.push_front(n2); if(n2.vKeys.size()>1) { vSizeAndPointerToNode.push_back(make_pair(n2.vKeys.size(),&lNodes.front())); lNodes.front().lit = lNodes.begin(); } } if(n3.vKeys.size()>0) { lNodes.push_front(n3); if(n3.vKeys.size()>1) { vSizeAndPointerToNode.push_back(make_pair(n3.vKeys.size(),&lNodes.front())); lNodes.front().lit = lNodes.begin(); } } if(n4.vKeys.size()>0) { lNodes.push_front(n4); if(n4.vKeys.size()>1) { vSizeAndPointerToNode.push_back(make_pair(n4.vKeys.size(),&lNodes.front())); lNodes.front().lit = lNodes.begin(); } } //删除母节点,在这里其实应该是一级子节点 lNodes.erase(vPrevSizeAndPointerToNode[j].second->lit); //判断是是否超过了需要的特征点数?是的话就退出,不是的话就继续这个分裂过程,直到刚刚达到或者超过要求的特征点个数 //作者的思想其实就是这样的,再分裂了一次之后判断下一次分裂是否会超过N,如果不是那么就放心大胆地全部进行分裂(因为少了一个判断因此 //其运算速度会稍微快一些),如果会那么就引导到这里进行最后一次分裂 if((int)lNodes.size()>=N) break; }//遍历vPrevSizeAndPointerToNode并对其中指定的node进行分裂,直到刚刚达到或者超过要求的特征点个数 //这里理想中应该是一个for循环就能够达成结束条件了,但是作者想的可能是,有些子节点所在的区域会没有特征点,因此很有可能一次for循环之后 //的数目还是不能够满足要求,所以还是需要判断结束条件并且再来一次 //判断是否达到了停止条件 if((int)lNodes.size()>=N || (int)lNodes.size()==prevSize) bFinish = true; }//一直进行不进行nToExpand累加的节点分裂过程,直到分裂后的nodes数目刚刚达到或者超过要求的特征点数目 }//当本次分裂后达不到结束条件但是再进行一次完整的分裂之后就可以达到结束条件时 }// 根据兴趣点分布,利用4叉树方法对图像进行划分区域 // Retain the best point in each node // Step 7 保留每个区域响应值最大的一个兴趣点 //使用这个vector来存储我们感兴趣的特征点的过滤结果 vector
vResultKeys; //调整大小为要提取的特征点数目 vResultKeys.reserve(nfeatures); //遍历这个节点列表 for(list
::iterator lit=lNodes.begin(); lit!=lNodes.end(); lit++) { //得到这个节点区域中的特征点容器句柄 vector
&vNodeKeys = lit->vKeys; //得到指向第一个特征点的指针,后面作为最大响应值对应的关键点 cv::KeyPoint* pKP = &vNodeKeys[0]; //用第1个关键点响应值初始化最大响应值 float maxResponse = pKP->response; //开始遍历这个节点区域中的特征点容器中的特征点,注意是从1开始哟,0已经用过了 for(size_t k=1;k<vNodeKeys.size();k++) { //更新最大响应值 if(vNodeKeys[k].response>maxResponse) { //更新pKP指向具有最大响应值的keypoints pKP = &vNodeKeys[k]; maxResponse = vNodeKeys[k].response; } } //将这个节点区域中的响应值最大的特征点加入最终结果容器 vResultKeys.push_back(*pKP); } //返回最终结果容器,其中保存有分裂出来的区域中,我们最感兴趣、响应值最大的特征点 return vResultKeys; }