1 概述

镜头透镜由于制造精度以及组装工艺的偏差会引入畸变，导致原始图像的失真，即图像畸变。

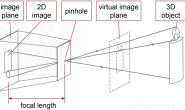
在前一篇文章《机器视觉模型——投影矩阵》中描述了机器视觉系统成像模型，在这个模型里包含了相机内参（与像元尺寸、焦距、像素中心有关）以及相机外参（与相机在世界坐标系的位姿有关），这个模型是一个理想模型，或者说线性模型，没有考虑到镜头透镜产生的畸变所带来的影响。结合上文成像模型，可以把畸变理解成像点和物点之间的光线是弯曲的，如下图所示。

图中本来应该共线的三个点 O、P_crt 、Q，现在由于透镜的某种偏差原因而不共线了，P_crt被成像在了 P P P点，很明显，此时的关系不再是前文讨论的矩阵关系了，也就是说，在畸变存在的条件下，用前文的矩阵公式计算出来的结果是不正确的。

所以，在用这个视觉模型矩阵公式前，需要先把产生的畸变消除掉，与前文同样原理，如果透镜畸变能用一个数学模型或者数学公式来表达，我们就可以很方便地消除畸变，我们把这个模型称为“畸变模型”。

2 透镜的畸变

透镜的畸变主要包括：径向畸变、切向畸变、薄透镜畸变等等，但最显著的是径向畸变和切向畸变，所以我们这个模型里只考虑这两种畸变。同时，图像的畸变是两种畸变的组合，因此把整个畸变分解为径向畸变分量和切向畸变分量。

2.1 径向畸变

径向畸变：就是沿着透镜半径方向分布的畸变，如我们所熟知的鱼眼镜头产生的畸变、枕形畸变、桶形畸变等。

下图为径向畸变的分布，一般越远离中心越严重。

由于这种畸变是从中心沿径向方向向外分布的，我们用r=0处的泰勒级数展开的前几项来近似描述径向畸变，径向畸变前后的坐标关系为

式中：

x_distorted ,y_distorted ——原畸变图像坐标

x,y——正确坐标（无畸变图像坐标，或校正后坐标）

r——半径， r² = x² + y²
k₁ , k₂ , k₃ ——引入的径向畸变参数

2.2 切向畸变

切向畸变：是由于透镜本身与相机传感器平面（像平面）或图像平面不平行而产生的，这种情况多是由于透镜被粘贴到镜头模组上的安装偏差导致，如下图所示。

随着相机制造工艺的大大提升，这种情况很少出现了，所以很多时候已经可以不考虑切向畸变。
下图为切向畸变的分布

切向畸变可以用两个额外的参数p1和p2来描述

式中：

x_distorted ,y_distorted ——原畸变图像坐标

x,y——正确坐标（无畸变图像坐标，或校正后坐标）

r——半径， r² = x² + y²

p₁​,p₂​——引入的切向畸变参数

3 机器视觉畸变模型

综上，可以得到机器视觉系统透镜畸变模型如下
畸变径向分量：

畸变切向分量：

其中包含了5个畸变参数： k₁ , k₂ , k₃ , p₁ , p₂。

对于一个给定的镜头成像系统，这5个畸变参数怎么获得？这就涉及到“相机标定”，即需要根据一系列已知的若干对原成像点与畸变成像点的坐标值，带入以上公式来解出，具体的限于篇幅这里不详细讨论。