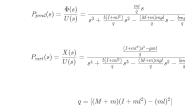四、稳定的定义与代数稳定判据
4.1 稳定的基本概念和线性系统稳定的充要条件
- 稳定是控制系统的重要性能,也是系统能够正常运行和工作的首要条件。控制系统在实际应用中应用的首要前提就是系统必须稳定。对系统进行各类品质指标的分析也必须在系统稳定的前提下进行。
- 控制系统在实际运行过程中,总会受到外界和内部一些因素的扰动,例如负载和能源的波动、系统参数的变化、环境条件的改变等。这些因素总是存在的,如果系统设计时不考虑这些因素,设计出来的系统不稳定,那这样的系统是不成功的,需要重新设计,或调整某些参数或结构。
- 如果系统不稳定,就会在任何微小的扰动作用下偏离原来的平衡状态,并随时间的推移而发散。因此,如何分析系统的稳定性并提出保证系统稳定的措施,是自动控制理论的基本任务之一。
- 其他:一个反馈条件要么是稳定的,要么是不稳定的—绝对稳定性。具有绝对稳定性的系统称为稳定系统;若一个闭环系统是稳定的,还可以用相对稳定性来进一步衡量其稳定程度。例如:飞机越稳定操作起来越困难。但是现代战斗机的相对不稳定性导致的结果就是良好的可操纵性,因此战斗机不如商业运输机飞行平稳,但是能够实现快速机动。
4.2 稳定的基本概念
定义1:系统处于某一起始的平衡状态。在外界扰动作用的影响下,偏离了该平衡状态。当外作用消失后,如果经过足够长的时间,这个系统还能恢复到原来的起始平衡状态,则称这样的系统为稳定的系统。否则为不稳定的系统。
不稳定的例子:
- 演播室音响系统的扬声器与麦克风之间的距离越近,回音越大,近到一定程度,啸叫盖过音响;(类似的现象还有电话机、电脑的麦克风等等);
稳定性反映在干扰消除之后过渡过程的性质上,系统与平衡状态的偏差可以认为是系统的初始偏差。
定义2:若控制系统在足够小的初始偏差作用下,其过渡过程的偏差随时间的推移逐渐趋于零,也即系统具有恢复原来平衡状态的能力,则称系统是稳定的;否则不稳定。
判断方法:判断传递函数的所有极点是否均位于左半平面,或等价地,判断系统矩阵
的特征值是否均位于
左半平面。若所有极点(或特征值)均位于
左半平面,就可以进一步通过极点(或特征值)的相对位置来判断相对稳定性。
注意事项:
1.稳定性是控制系统自身的固有性质,这稳定性取决于系统的固有特征(结构、参数),与系统的输入信号无关;
A:对线性系统,系统是大范围稳定的(与输入偏差无关);
B:对实际“小偏差线性化”的近似线性系统,偏差达到一定范围后,系统不再稳定。
2.稳定性指的是自由震荡之下的稳定性,即输入为零,系统在初始偏差不为零时的稳定性;也即是讨论自由振荡是收敛还是发散。
4.3 系统稳定的充要条件
设系统或环节的微分方程为:
式中:——输入,
——输出,
;
为常系数。
将上式求拉式变换,得:
即有:
扰动信号的作用相当于对系统的一个脉冲响应信号,系统的输出增量(偏差值)即是脉冲输入的响应
。
对于具有以上传递函数的控制系统来说,脉冲输入的拉式变换为1,即,所以系统输出增量的拉式变换为:
线性系统稳定的充要条件:
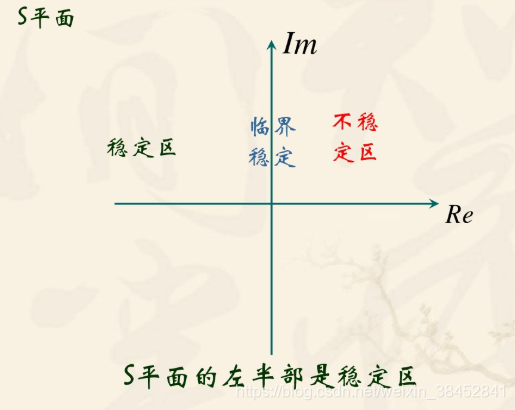
系统特征方程的根(即传递函数的极点)全为负实数或具有负实部的共轭复根。或者说,特征方程的根应全部位于左半平面。
- 如果特征方程中有一对实部为正的共轭复根,它的对应项是发散的周期振荡;
- 如果特征方程中有一个正实根,它所对应的指数项将随时间单调增长。
上述两种情况下系统是不稳定的。
- 如果特征方程中有一个实根,它所对应于一个常数项,系统可在任何状态下平衡,称为随遇平衡状态;
- 如果特征方程中有一对共轭虚根,对应于等幅的周期振荡,称为临界平衡状态(或临界稳定状态)。
从控制工程的角度认为临界稳定状态和随遇平衡状态属于不稳定。
注意:
稳定性是线性定常系统的一个属性,只与系统本身的结构参数有关,与输入输出信号无关,与初始条件无关;只与极点有关,与零点无关。
1.对于一阶系统:
,
只要都大于零,系统就是稳定的。
2.对于二阶系统:
,
只有都大于零,系统才稳定(负实根或实部为负)。
对于三阶或以上系统,求根是很繁琐的。于是就有了以下的代数稳定性判据。
4.4 代数稳定性判据
4.4.1 劳斯稳定性判据
设线性系统的闭环特征方程为:
则该系统稳定的条件为:
a.特征方程的各项系数都不等于零;
b.特征方程的各项系数的符号都相同。
此两项为必要条件。
例如:
充分条件:由特征方程系数组成的劳斯排列阵的第一列的所有项均为正。
充要条件:对于稳定系统而言,劳斯排列阵的第一列中,应该没有符号变化。


这种过程需一直进行到第n行被算完为止,系数的完整阵列呈现一个倒三角形。
注意:
为简化计算,可用一个正整数去除或乘某一整个行,并不改变稳定性结论。
劳斯稳定判据:
劳斯稳定判据是很根据所列劳斯表第一列系数符号的变化,去判别特征方程式根在平面上的具体分布,过程如下:
- 如果劳斯表中第一列的系数均为正值,则其特征方程式的根都在的左半平面,相应的系统是稳定的。
- 如果劳斯表中第一列系数的符号有变化,其变化的次数等于该特征方程式的根在的右半平面上的个数,相应的系统为不稳定。
具体劳斯-赫尔维茨稳定性判据链接可以参考如下链接:https://wenku.baidu.com/view/e5fb484f6ad97f192279168884868762cbaebb17.html