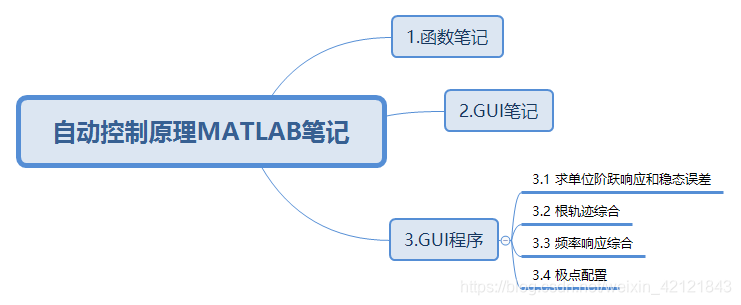
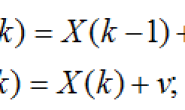全文框架
1.函数笔记
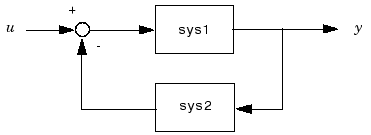
tf():传递函数 sys = tf(Numerator,Denominator) 创建传递函数,numerator为分子向量,denominator为分母向量 后面可加参数,如:‘Variable’,‘p’,意思是把p作为变量 若要从传递函数中取得分子分母向量,可以用:num1=sys.num{1},不能用numden等函数,因为其不能用于tf结构体 另外,开闭环传递函数之间的转换,务必用feedback,若直接用公式Gs=Gk(s)/(1+Gk(s)H(s))会有错误 ss():状态空间方程 sys = ss(A,B,C,D) A,B,C,D为状态空间方程的四个矩阵 ss2tf():状态空间方程转系统函数 [num,den] = ss2tf(A,B,C,D) Num为分子,den为分母 dcgain():获取稳态值 dc=dcgain(sys) feedback():反馈 sys = feedback(sys1,sys2)
 rlocus(): 求根轨迹 rlocus(sys):绘制根轨迹图 r = rlocus(sys,k):指定增益,返回r为与k对应的根轨迹点 [r,k] = rlocus(sys):同上,但系统会自动选择根轨迹向量。 Sgrid():绘制等ξ,ω网格线 sgrid(z,wn)z为阻尼比,wn为无阻尼自然频率 rlocfind():求根轨迹上指定点 [k,p]=rlocfind(sys) K为增益,p为极点坐标,需要用鼠标点击根轨迹上相应的点。同时也会返回被选极点的开环增益K和与之对应的所有其他闭环极点的值 Zp2tf():零极点转化为传递函数 [b,a] = zp2tf(z,p,k) 输入零极点向量和增益,输出传递函数的分子分母向量:
rlocus(): 求根轨迹 rlocus(sys):绘制根轨迹图 r = rlocus(sys,k):指定增益,返回r为与k对应的根轨迹点 [r,k] = rlocus(sys):同上,但系统会自动选择根轨迹向量。 Sgrid():绘制等ξ,ω网格线 sgrid(z,wn)z为阻尼比,wn为无阻尼自然频率 rlocfind():求根轨迹上指定点 [k,p]=rlocfind(sys) K为增益,p为极点坐标,需要用鼠标点击根轨迹上相应的点。同时也会返回被选极点的开环增益K和与之对应的所有其他闭环极点的值 Zp2tf():零极点转化为传递函数 [b,a] = zp2tf(z,p,k) 输入零极点向量和增益,输出传递函数的分子分母向量:
 Pzmap():求零极点分布 pzmap(sys):在坐标轴上标出零极点 [p,z] = pzmap(sys):返回系统sys的零点向量z和极点向量p bode(): 绘制bode图 bode(sys):显示系统sys的bode图 [mag,phase,wout] = bode(sys):返回幅值,相位以及对应的角频率w nyquist():绘制极坐标图 nyquist(sys):显示系统的奈奎斯特图
Pzmap():求零极点分布 pzmap(sys):在坐标轴上标出零极点 [p,z] = pzmap(sys):返回系统sys的零点向量z和极点向量p bode(): 绘制bode图 bode(sys):显示系统sys的bode图 [mag,phase,wout] = bode(sys):返回幅值,相位以及对应的角频率w nyquist():绘制极坐标图 nyquist(sys):显示系统的奈奎斯特图
2.GUI笔记
2.1控件 1.静态文本(Static Text) 2.编辑框(Edit Text)控件 3.列表框(Listbox)控件 4.滚动条(Slider)控件 5.按钮(Push Button)控件 6.开关按钮(Toggle Button)控件 7.单选按钮(Radio Button)控件 8.按钮组(Button Group)控件 9.检查框(Check Box)控件 10.列表框(Listbox)控件 11.弹出式菜单(Popup Menu)控件 12.坐标轴(Axes)控件 13.面板(Panel)控件 每一个控件都有自己的属性常规属性有: 控件风格和外观 (1)BackgroundColor:设置控件背景颜色,使用[R G B]或颜色定义。 (2)CData:在控件上显示的真彩色图像,使用矩阵表示。 (3)ForegroundColor:文本颜色。 (4)String属性:控件上的文本,以及列表框和弹出菜单的选项。 (5)Visible:控件是否可见。 对象的常规信息 (1)Enable属性: 表示此控件的使能状态,设置为on”,表示可选,为“off”时则表示不可选。 (2)Style:控件对象类型。 (3)Tag:控件表示(用户定义)。 (4)TooltipString属性:提示信息显示。当鼠标指针位于此控件上时,显示提示信息。 (5)UserData:用户指定数据。 (6)Position:控件对象的尺寸和位置。 (7)Units:设置控件的位置及大小的单位 (8)有关字体的属性,如 FontAngle, FontName等。 控件回调函数的执行 (1)BusyAction:处理回调函数的中断。有两种选项:即Cancel:取消中断事件,queue:排队(默认设置)。 (2)ButtonDownFcn属性:按钮按下时的处理函数。 (3)CallBack属性:是连接程序界面整个程序系统的实质性功能的纽带。该属性值应该为一个可以直接求值的字符串,在该对象被选中和改变时,系统将自动地对字符串进行求值。 (4)CreateFcn:在对象产生过程中执行的回调函数。 (5)DeleteFcn:删除对象过程中执行的回调函数。 (6)Interruptible属性:指定当前的回调函数在执行时是否允许中断,去执行其他的函数。 控件当前状态信息 (1)ListboxTop:在列表框中显示的最顶层的字符串的索引。 (2)Max:最大值。 (3)Min:最小值。 (4)Value:控件的当前值。你可以使用属性编辑器来设置属性 2.2 回调函数 :CallBack 每个控件都有几种回调函数,右键选中的控件一般会有如下菜单: 然后就可以跳转到相应的 Editor中编辑代码,GUIDE会自动生成 相应的函数体,函数名,名称一般是 控件 Tag+ Call类型名 参数有三个 ( hObject, eventdata, handles) 其中 hObject 为发生事件的源控件,eventdata为事件数据结构,handles为传入的对象句柄 CreateFcn 是在控件对象创建的时候发生(一般为初始化样式,颜色,初始值等) DeleteFcn 实在空间对象被清除的时候发生 ButtonDownFcn和KeyPressFcn分别为鼠标点击和按键事件Callback CallBack为一般回调函数,因不同的控件而已异。例如按钮被按下时发生,下拉框改变值时发生,sliderbar 拖动时发生等等。 2.3 绘图 1.figure函数:创建一个新的图形对象。 2.newplot函数:做好开始画新图形对象的准备。 3.axes函数:创建坐标轴图形对象。 4.line函数:画线。 5.patch函数:填充多边形。 6.surface函数:绘制三维曲面。 7.image函数:显示图片对象。 8.uicontrol函数:生成用户控制图形对象。 9.uimenu函数:生成图形窗口的菜单中层次菜单与下一级子菜单。 几个实用的小函数: uigetfile 选择文件对话框 uiputfile 保存文件对话框 uisetcolor 设置颜色对话框 fontsetcolor 设置字体对话框 msgbox 消息框 warndlg 警告框 helpdlg 消息框 打开新窗口首先创建一个计算窗口界面test2.flg,和父窗口放在同一个文件夹下 在.m文件中的计算按钮函数里添加语句: open(‘test2.fig’) h = guihandles;%为新定义的窗口设置句柄变量h set(h.text,‘string’,结果变量名)%text为输出控件名 不过如果要让父窗口不可用,你需要使用uiwait来定焦于用户对话框。 例如: h=helpdlg(‘Please press me!’,‘Attention’); uiwait(h); 在某一坐标轴上作图 h=guihandles; axes(h.axes1); plot(y); 注意,每次在旧的坐标轴上画新图的时候,务必清除坐标轴,否则会显示找不到axes 2.4 获取与设置对象属性 常用函数: gcf函数:获得当前图形窗口的句柄 gca函数:获得当前坐标轴的句柄 gco函数:获得当前对象的句柄 gcbo函数:获得当前正在执行调用的对象的句柄 gcbf函数:获取包括正在执行调用的对象的图形句柄 delete函数:删除句柄所对应的图形对象 findobj函数:查找具有某种属性的图形对象 设置方法: (1)get函数返回某些对象属性的当前值。例如: p=get(obj,‘Position’); (2)函数set改变句柄图形对象属性,例如: set(obj,‘Position’,vect); 2.5 部分函数笔记 部分字符串处理函数:







 v = get(h,propertyName) h. v is a structure whose field names are the property names propertyName, returns the value for the specific property, eg: ‘Color’ ‘LineWidth’ ‘string’… set(H,Name,Value) specifies a value for the property Name on the object identified by H. 字符串类型:Char 和 String 假如str为char,则可用str(1),str(2)等来求字符串元素,下标从0开始。String同理。 从一串带空格的字符串里分离出数字:(如输入 12 23 45)
v = get(h,propertyName) h. v is a structure whose field names are the property names propertyName, returns the value for the specific property, eg: ‘Color’ ‘LineWidth’ ‘string’… set(H,Name,Value) specifies a value for the property Name on the object identified by H. 字符串类型:Char 和 String 假如str为char,则可用str(1),str(2)等来求字符串元素,下标从0开始。String同理。 从一串带空格的字符串里分离出数字:(如输入 12 23 45)
t='';
str1=get(handles.edit1,'String');
n=length(str1);
j=1;
num=strings;%字符串数组
for i=1:n
if(str1(i)~=' ')
t=strcat(t,str1(i));
else
num(j)=t;
j=j+1;
t='';
end
end
从输入框里获取矩阵:
matrix=str2num(get(handles.edit,'string'));
3.GUI程序
3.1求单位阶跃响应及稳态误差
一、题目及要求: 1、由用户输入被控系统的模型(含传递函数模型和状态空间模型); 2、根据闭环系统单位阶跃响应计算系统的超调量、峰值时间和调整时间,并输出显示计算结果; 3、计算闭环系统的稳态误差并输出显示计算结果; 4、输出并显示闭环系统的单位阶跃响应曲线。 二、运行结果 输入开环传递函数:

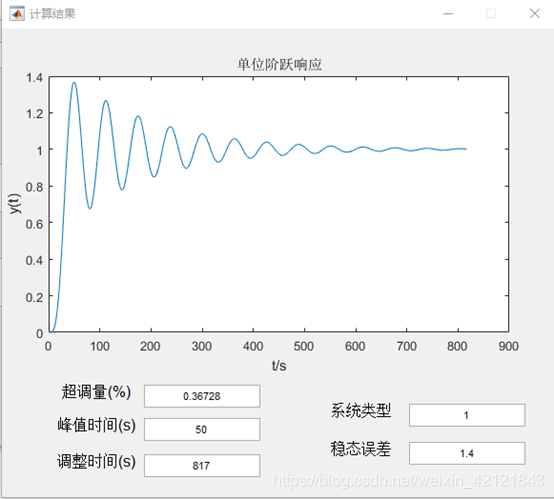 输入状态空间模型:
输入状态空间模型:
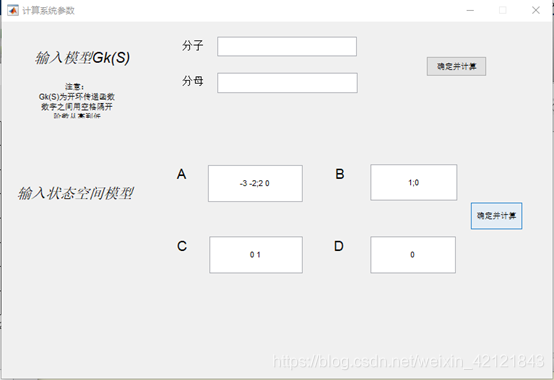
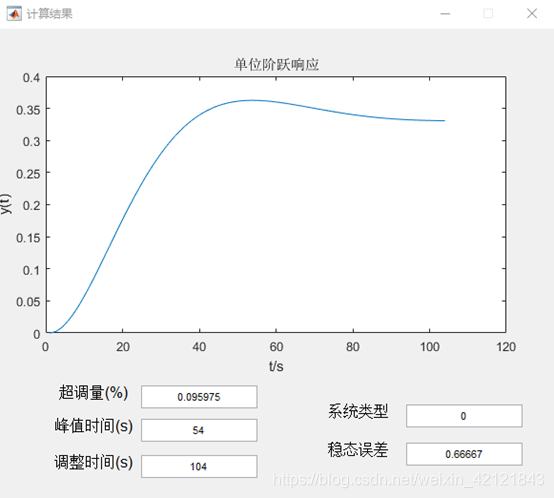 三、代码 求开环函数性能的代码:
三、代码 求开环函数性能的代码:
function pushbutton1_Callback(hObject, eventdata, handles)
t='';
h1=guihandles;
str1=get(h1.edit1,'String');
str2=get(h1.edit2,'String');
n=length(str1);
m=length(str2);
j=1;
num=[];%分子
den=[];%分母
for i=1:n
if(str1(i)~=' ')
t=strcat(t,str1(i));
else
num(j)=str2double(t);
j=j+1;
t='';
end
if(i==n)
num(j)=str2double(t);
end
end
t='';
j=1;
for i=1:m
if(str2(i)~=' ')
t=strcat(t,str2(i));
else
den(j)=str2double(t);
j=j+1;
t='';
end
if(i==m)
den(j)=str2double(t);
end
end
GkS=tf(num,den)%开环函数
GS=GkS/(1+GkS)%闭环函数,默认单位反馈
[y1 t]=step(GS);%单位阶跃响应
mp=max(y1);
%峰值时间
tp=find(y1==mp)
cs=length(t);
%稳态值
yss=y1(cs)
%超调量
ct=(mp - yss)/yss
%调整时间
s=cs;
while y1(s)>0.98*yss&y1(s)<1.02*yss
s=s-1;
end;
ts=s
open('output.fig');
h2=guihandles;
set(h2.edit1,'string',string(ct));
set(h2.edit2,'string',string(tp));
set(h2.edit3,'string',string(cs));
plot(h2.axes1,y1);title('单位阶跃响应');xlabel('t/s');ylabel('y(t)');
%稳态误差
I=0;%系统类型
K_p=dcgain(GkS);
num1=num;
num1(length(num)+1)=0;
sGkS=tf(num1,den);
K_v=dcgain(sGkS);
num2=num1;
num2(length(num1)+1)=0;
s2GkS=tf(num2,den);
K_a=dcgain(s2GkS);
if(K_p~=0&&K_p~=inf)
I=0;
e_sr=1/(1+K_p);%单位阶跃输入时
elseif(K_v~=0&&K_v~=inf)
I=1;
e_sr=1/K_v;
elseif(K_a~=0&&K_a~=inf)
I=2;
e_sr=1/K_a;
else
end
set(h2.edit4,'string',string(I));
set(h2.edit5,'string',string(e_sr));
状态空间模型输入:
h1=guihandles;
A=str2num(get(h1.edit3,'string'));
B=str2num(get(h1.edit4,'string'));
C=str2num(get(h1.edit6,'string'));
D=str2num(get(h1.edit5,'string'));
[num den]=ss2tf(A,B,C,D);
GkS=tf(num,den)%系统函数
%%%%%%%%%%%%%%后面省略,因转化为系统函数了,后面操作和上面程序相同
3.2根轨迹综合
一、题目及要求:
 二、运行结果 主界面,输入开环传递函数与根轨迹综合指标
二、运行结果 主界面,输入开环传递函数与根轨迹综合指标
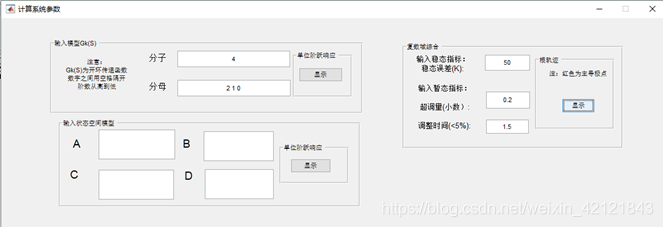 显示单位阶跃响应
显示单位阶跃响应
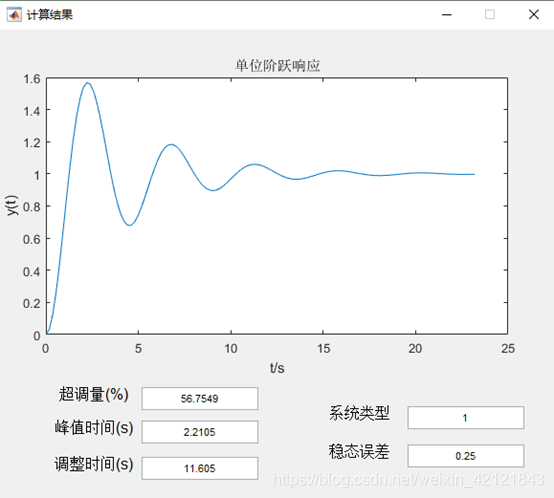 输入性能指标,进入综合界面
输入性能指标,进入综合界面
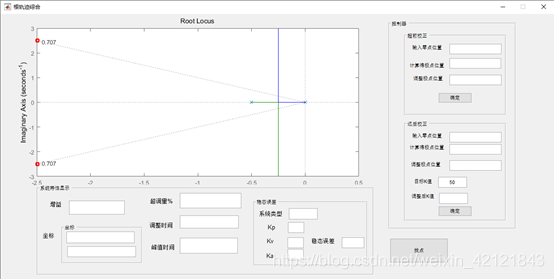 超前校正
超前校正
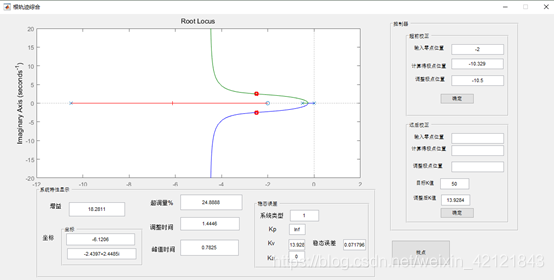 迟后校正
迟后校正
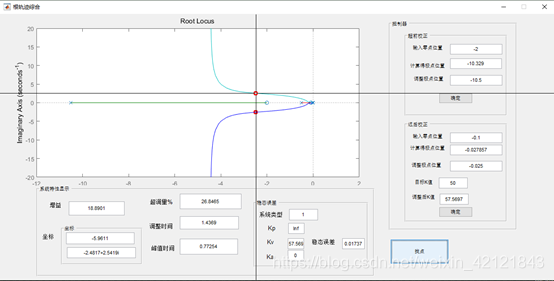 校正后阶跃响应
校正后阶跃响应
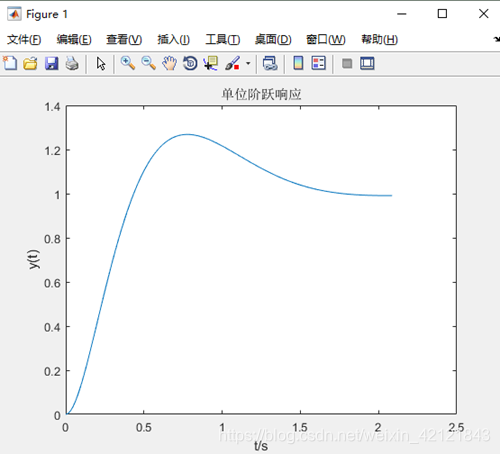 三、代码 显示单位阶跃响应代码:
三、代码 显示单位阶跃响应代码:
function pushbutton1_Callback(hObject, eventdata, handles)
global h1;
h1=guihandles;
t='';
str1=get(h1.edit1,'String');
str2=get(h1.edit2,'String');
n=length(str1);
m=length(str2);
j=1;
num=[];%分子
den=[];%分母
for i=1:n
if(str1(i)~=' ')
t=strcat(t,str1(i));
else
num(j)=str2double(t);
j=j+1;
t='';
end
if(i==n)
num(j)=str2double(t);
end
end
t='';
j=1;
for i=1:m
if(str2(i)~=' ')
t=strcat(t,str2(i));
else
den(j)=str2double(t);
j=j+1;
t='';
end
if(i==m)
den(j)=str2double(t);
end
end
global GkS GkS_original;
GkS=tf(num,den)%开环函数
GkS_original=GkS;
GS=feedback(GkS,1)%闭环函数,默认单位反馈
[y1 t]=step(GS);%单位阶跃响应
open('output.fig');
h2=guihandles;
plot(h2.axes1,t,y1);title('单位阶跃响应');xlabel('t/s');ylabel('y(t)');
mp=max(y1);
%峰值时间
tp=t(find(y1==mp));%注意:step返回的t为时间序列,但间隔并不为1s,find只是找到时间序列中的位置,并非时间本身
% cs=length(t);%此算法错误,t序列长度并非t本身
% yss=y1(cs)%稳态值
y_dc=dcgain(GS);
%超调量
ct=(mp - y_dc)/y_dc;
ct=ct*100;
%调整时间
i=length(t);
while y1(i)>0.95*y_dc&y1(i)<1.05*y_dc
i=i-1;
end;
ts=t(i);
set(h2.edit1,'string',string(ct));
set(h2.edit2,'string',string(tp));
set(h2.edit3,'string',string(ts));
%稳态误差
I=0;%系统类型
K_p=dcgain(GkS);
num1=num;
num1(length(num)+1)=0;
sGkS=tf(num1,den);
K_v=dcgain(sGkS);
num2=num1;
num2(length(num1)+1)=0;
s2GkS=tf(num2,den);
K_a=dcgain(s2GkS);
if(K_p~=0&&K_p~=inf)
I=0;
e_sr=1/(1+K_p);%单位阶跃输入时
elseif(K_v~=0&&K_v~=inf)
I=1;
e_sr=1/K_v;
elseif(K_a~=0&&K_a~=inf)
I=2;
e_sr=1/K_a;
else
end
set(h2.edit4,'string',string(I));
set(h2.edit5,'string',string(e_sr));
显示根轨迹图的代码
function pushbutton4_Callback(hObject, eventdata, handles)
h1=guihandles;
global GkS GkS_original p z p1 p2;
k_need=str2num(get(h1.edit7,'String'));
sigma_need=str2num(get(h1.edit8,'String'));
kesai_need=log(1/sigma_need)/(pi^2+(log(1/sigma_need))^2)^0.5;
kesai_need=kesai_need+0.15;%留裕量
ts_need=str2num(get(h1.edit9,'String'));
wn_need=3/(kesai_need*ts_need);
wn_need=wn_need+0.5;%留裕量
p1=-kesai_need*wn_need+i*wn_need*(1-kesai_need^2)^0.5;
p2=-kesai_need*wn_need-i*wn_need*(1-kesai_need^2)^0.5;%主导极点
global Gc_d Gc_i;
Gc_d=1;%控制器初始化
Gc_i=1;
GkS=GkS_original;
open('rlocus1.fig');
h3=guihandles;
set(h3.edit13,'string',string(k_need));
axes(h3.axes1);
plot(p1,'square','LineWidth',2,'MarkerEdgeColor','r');hold on
plot(p2,'square','LineWidth',2,'MarkerEdgeColor','r');hold on;%主导极点设为红色
[p,z]=pzmap(GkS);
rlocus(GkS);
sgrid(0.707,10);
在根轨迹图上显示点的详细信息
function pushbutton1_Callback(hObject, eventdata, handles)
global GkS;
close (figure(1));
h3=guihandles;
[k,p]=rlocfind(GkS);
set(h3.edit1,'string',string(k));
set(h3.edit2,'string',string(p(1)));
set(h3.edit7,'string',string(p(2)));
GkS_2=k*GkS;
GS=feedback(GkS_2,1);%闭环函数,默认单位反馈
[y1 t]=step(GS);%单位阶跃响应
figure(1)
plot(t,y1);title('单位阶跃响应');xlabel('t/s');ylabel('y(t)');
mp=max(y1);
%稳态值
y_dc=dcgain(GS);
if(abs(y_dc-mp)>0.01)%判断是否为过阻尼状态
%峰值时间
tp=t(find(y1==mp));
%超调量
ct=(mp - y_dc)/y_dc;
ct=ct*100;
else
tp=0;
ct=0;
end
%调整时间
i=length(t);
while y1(i)>0.95*y_dc&y1(i)<1.05*y_dc
i=i-1;
end;
ts=t(i);
set(h3.edit3,'string',string(ct));
set(h3.edit4,'string',string(ts));
set(h3.edit5,'string',string(tp));
%稳态误差
I=0;%系统类型
K_p=dcgain(GkS_2);
num1=GkS_2.num{1};
den=GkS_2.den{1};
num1(length(num1)+1)=0;
sGkS=tf(num1,den);
K_v=dcgain(sGkS);
num2=num1;
num2(length(num1)+1)=0;
s2GkS=tf(num2,den);
K_a=dcgain(s2GkS);
if(K_p~=0&&K_p~=inf)
Kout=K_p;
I=0;
e_sr=1/(1+K_p);%单位阶跃输入时
elseif(K_v~=0&&K_v~=inf)
Kout=K_v;
I=1;
e_sr=1/K_v;
elseif(K_a~=0&&K_a~=inf)
Kout=K_a;
I=2;
e_sr=1/K_a;
else
end
set(h3.edit8,'string',string(I));
set(h3.edit17,'string',string(K_p));
set(h3.edit15,'string',string(K_v));
set(h3.edit16,'string',string(K_a));
set(h3.edit6,'string',string(e_sr));
set(h3.edit14,'string',string(Kout));
超前校正代码
function pushbutton2_Callback(hObject, eventdata, handles)
h3=guihandles;
global p1 p2 Gc_d GkS GkS_original Gc_i;
pd=str2num(get(h3.edit10,'String'));
zd=str2num(get(h3.edit9,'String'));
Gc_d=tf([1 -zd],[1 -pd]);
GkS=GkS_original*Gc_d*Gc_i;
%%%%%%%%%%%%%%%%%%%%%%%%%%%不可取,因为只是通过零极点得到的开环传递函数,不是串联校正
%global p z
% p_1=p;
% length_p=length(p);
% p_1(length_p+1)=pd;
% z_1=z;
% length_z=length(z);
% z_1(length_z+1)=zd;
% [num,den]=zp2tf(z_1,p_1,1);
% GkS_d=tf(num,den);
cla
plot(p1,'square','LineWidth',2,'MarkerEdgeColor','r');hold on
plot(p2,'square','LineWidth',2,'MarkerEdgeColor','r');hold on
rlocus(GkS);
超前校正中:幅角条件算法
function edit9_Callback(hObject, eventdata, handles)
global z p p1;
h3=guihandles;
zd=str2num(get(h3.edit9,'String'));
%%%%%%%%%%%通过幅角条件算极点位置
angle_p=0;
angle_z=0;
for i=1:length(p)
angle_p=angle_p+rad2deg(angle(p1-p(i)));
end
for i=1:length(z)
angle_z=angle_z+rad2deg(angle(p1-z(i)));
end
angle_z=angle_z+rad2deg(angle(p1-zd));%超前控制零点的幅角
% angle_p=angle_p+rad2deg(angle(p1-pd));
angle_zd=angle_z-angle_p+180;
if(angle_zd>3&&angle_zd<90)
x_zd=real(p1)-imag(p1)/tan(deg2rad(angle_zd));
set(h3.edit18,'string',string(x_zd));
else
set(h3.edit18,'string',string('ERROR'));
end
迟后校正代码
function pushbutton3_Callback(hObject, eventdata, handles)
h3=guihandles;
global p1 p2 Gc_d Gc_i GkS GkS_original Kout;
pi=str2num(get(h3.edit12,'String'));
zi=str2num(get(h3.edit11,'String'));
Gc_i=tf([1 -zi],[1 -pi]);
GkS=GkS_original*Gc_d*Gc_i;
cla
plot(p1,'square','LineWidth',2,'MarkerEdgeColor','r');hold on
plot(p2,'square','LineWidth',2,'MarkerEdgeColor','r');hold on
rlocus(GkS);
迟后校正:求偶极子
function edit11_Callback(hObject, eventdata, handles)
global k_need Kout;
h3=guihandles;
zi=str2num(get(h3.edit11,'String'));
ratio=k_need./Kout;
pi=zi/ratio;
if(pi<0)
set(h3.edit19,'string',string(pi));
else
set(h3.edit19,'string',string('ERROR'));
end
3.3频率响应综合
一、题目及要求:
 二、运行结果 输入开环传递函数
二、运行结果 输入开环传递函数
 未综合系统的单位阶跃响应
未综合系统的单位阶跃响应
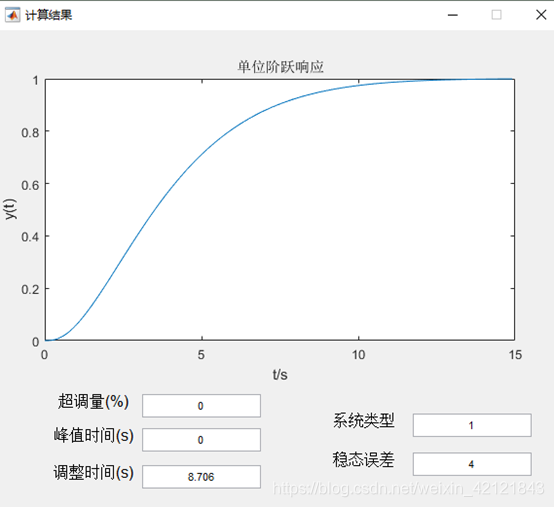 输入稳态和暂态指标
输入稳态和暂态指标
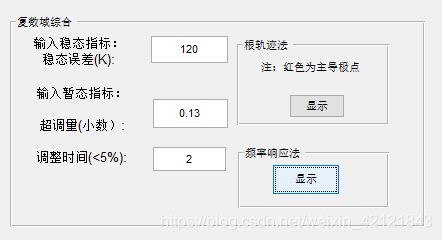 输入参数显示bode图
输入参数显示bode图
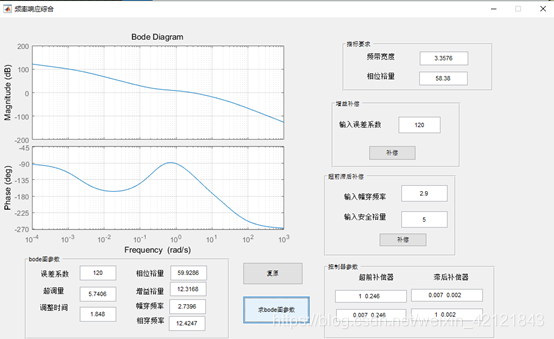 调整后系统的单位阶跃响应
调整后系统的单位阶跃响应
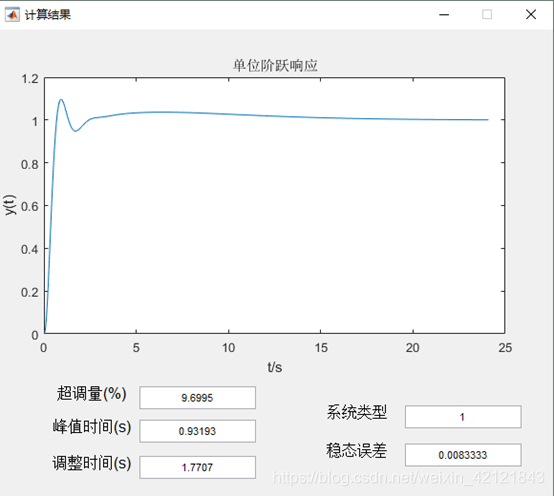 三、代码 计算相位裕量,频带宽度以及显示bode图
三、代码 计算相位裕量,频带宽度以及显示bode图
function pushbutton6_Callback(hObject, eventdata, handles)
global GkS k_need sigma_need ts_need phym;
h1=guihandles;
k_need=str2num(get(h1.edit7,'String'));
sigma_need=str2num(get(h1.edit8,'String'));
ts_need=str2num(get(h1.edit9,'String'));
kesai_need=log(1/sigma_need)/(pi^2+(log(1/sigma_need))^2)^0.5;
wn_need=3/(kesai_need*ts_need);
%%%求相位裕量
r = atan(2*kesai_need/(sqrt(sqrt(1+kesai_need^4)-2*kesai_need*kesai_need)));
phym=rad2deg(r);
%求频带宽度
wbw = wn_need*sqrt((1-2*kesai_need*kesai_need)+sqrt(4*kesai_need^4-4*kesai_need^2+2));
open('frequency.fig');
h4=guihandles;
axes(h4.axes2);
GS=feedback(GkS,1);
bode(GkS);grid;
set(h4.edit3,'string',string(k_need));
set(h4.edit2,'string',string(phym));
set(h4.edit1,'string',string(wbw));
超前滞后补偿器的计算
function pushbutton3_Callback(hObject, eventdata, handles)
global GkS GkS_original phym Gc Gd;
h4=guihandles;
wc=str2num(get(h4.edit12,'string'));%幅穿频率
x=str2num(get(h4.edit13,'string'));%安全裕量
[ mag,phase ] = bode( GkS,wc );%在幅穿频率处的相位
phase = phase +180;
phy = deg2rad( phym - phase + x ); %超前补偿器需要提供的超前相位,角度转换为弧度制
B = ( 1-sin( phy ))/( 1+sin( phy ) ); % β
T1 = 1/(wc*sqrt( B )); %超前补偿器低段转折频率
Gc = tf( 1,B )*tf( [1,1/T1],[ 1,1/(B*T1) ] ); %超前补偿器传递函数
w2 = wc/10; %滞后补偿器高段转折频率
Gd = tf( B,1 )*tf( [1,w2],[ 1,B*w2 ] ); %滞后补偿器传递函数
GkS = GkS*Gd*Gc; %超前-滞后综合
cla
bode(GkS);grid;
增益补偿
function pushbutton1_Callback(hObject, eventdata, handles)
global GkS I K_p K_v K_a k_need GkS_original;
h4=guihandles;
if(I==0)
K=K_p;
elseif(I==1)
K=K_v;
elseif(I==2)
K=K_a;
else
end
k_need=str2num(get(h4.edit3,'string'));
k_add=k_need/K;
GkS=tf(k_add,1)*GkS;
cla
bode(GkS);grid;
显示单位阶跃响应,bode图参数以及补偿器参数
function pushbutton2_Callback(hObject, eventdata, handles)
global GkS;
h4=guihandles;
GS=feedback(GkS,1)%闭环函数,默认单位反馈
[y1 t]=step(GS);%单位阶跃响应
open('output.fig');
h2=guihandles;
plot(h2.axes1,t,y1);title('单位阶跃响应');xlabel('t/s');ylabel('y(t)');
%%%%%%%%%%%%%判断系统稳定性
[p z]=pzmap(GS);
for i=1:length(p)
if(p(i)>0)
warndlg('系统不稳定','ERROR');
return
end
end
mp=max(y1);
%峰值时间
tp=t(find(y1==mp));%注意:step返回的t为时间序列,但间隔并不为1s,find只是找到时间序列中的位置,并非时间本身
y_dc=dcgain(GS);
if(abs(y_dc-mp)>0.01)%判断是否为过阻尼状态
%峰值时间
tp=t(find(y1==mp));
%超调量
ct=(mp - y_dc)/y_dc;
ct=ct*100;
else
tp=0;
ct=0;
end
%调整时间
i=length(t);
while y1(i)>0.95*y_dc&y1(i)<1.05*y_dc
i=i-1;
end;
ts=t(i);
set(h2.edit1,'string',string(ct));
set(h2.edit2,'string',string(tp));
set(h2.edit3,'string',string(ts));
%稳态误差
I=0;%系统类型
K_p=dcgain(GkS);
num=GkS.num{1,1};%求GkS的分子和分母
den=GkS.den{1,1};
num1=num;
num1(length(num)+1)=0;
sGkS=tf(num1,den);
K_v=dcgain(sGkS);
num2=num1;
num2(length(num1)+1)=0;
s2GkS=tf(num2,den);
K_a=dcgain(s2GkS);
if(K_p~=0&&K_p~=inf)
I=0;
kk=K_p;
e_sr=1/(1+K_p);%单位阶跃输入时
elseif(K_v~=0&&K_v~=inf)
I=1;
kk=K_v;
e_sr=1/K_v;
elseif(K_a~=0&&K_a~=inf)
I=2;
kk=K_a;
e_sr=1/K_a;
else
end
set(h2.edit4,'string',string(I));
set(h2.edit5,'string',string(e_sr));
set(h4.edit4,'string',string(kk));
set(h4.edit6,'string',string(ct));
set(h4.edit7,'string',string(ts));
[gm,pm,wg,wc]=margin(GkS);
set(h4.edit8,'string',string(pm));
set(h4.edit9,'string',string(gm));
set(h4.edit10,'string',string(wc));
set(h4.edit11,'string',string(wg));
global Gc Gd;
num1=round(Gc.num{1,1},3);
set(h4.edit14,'string',sprintf('%g ',num1));
den1=round(Gc.den{1,1},3);
set(h4.edit15,'string',sprintf('%g ',den1));
num2=round(Gd.num{1,1},3);
set(h4.edit16,'string',sprintf('%g ',num2));
den2=round(Gd.den{1,1},3);
set(h4.edit17,'string',sprintf('%g ',den2));
3.4极点配置
一、题目及要求:
 二、运行结果 输入状态空间模型
二、运行结果 输入状态空间模型
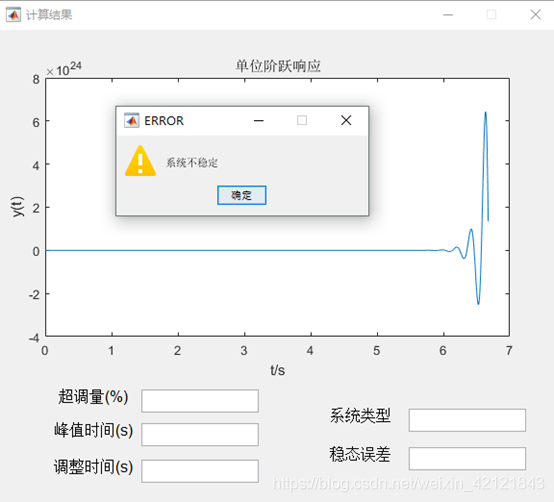
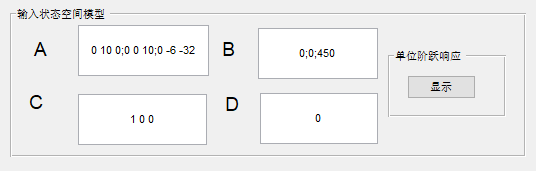 显示单位阶跃响应
显示单位阶跃响应
 输入配置极点
输入配置极点
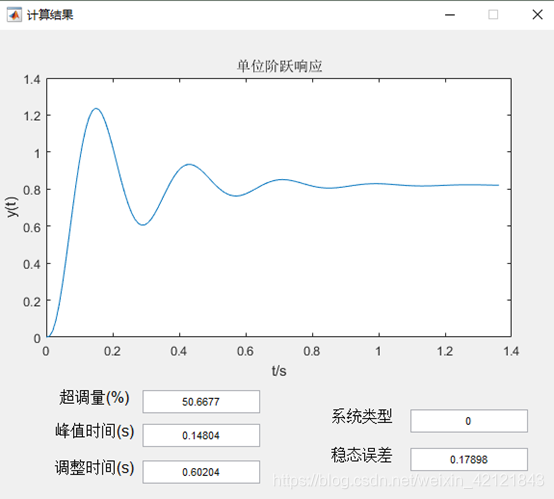
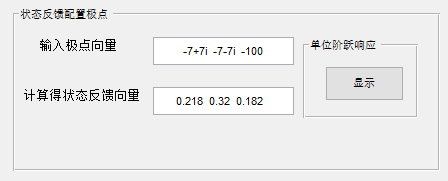 配置极点后的单位阶跃响应
配置极点后的单位阶跃响应
 三、代码 显示状态反馈向量:(要求不能用place函数,这里用Ackermann公式求解)
三、代码 显示状态反馈向量:(要求不能用place函数,这里用Ackermann公式求解)
function edit18_Callback(hObject, eventdata, handles)
global A B A_SF;
h1=guihandles;
lambda=str2num(get(h1.edit18,'string'));
lambda_need=charpoly(diag(lambda));
% n=rank(A);%A有可能不满秩,最好用length
n=length(A);
if(rank(ctrb(A,B))~=length(A))
warndlg('ERROR','系统不完全能控');
return
end
Q_c=ctrb(A,B);
Q_ct=inv(Q_c);
q_t=Q_ct(n,:);
k=eye(n)*lambda_need(n+1);
for i=1:n
k=k+A^i*lambda_need(n+1-i);
end
k=q_t*k;
k=round(k,3);
A_SF=A-B*k;
set(h1.edit19,'string',sprintf('%g ',k));
总结
通过matlab编程,对自动控制原理有了更深刻的了解,也锻炼了编程能力。 继续加油。