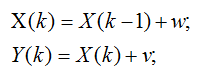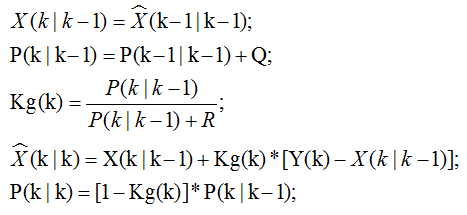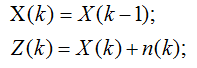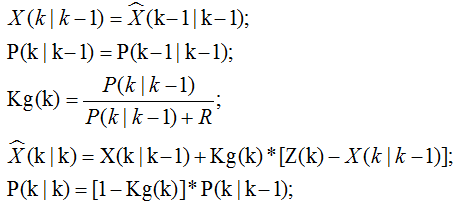通过实例来学习可以说是最快的了,这里开始就是实例了!
理论请看前一篇文章:Kalman滤波器的应用解释1
目录
例子1.普遍文章里温度的例子
例子2.论文中测距的例子
例子3.观测函数为y=5x
例子4:小车做匀速直线运动
1. 首先建立小车的状态转移模型
2.然后建立小车的观测模型
3.得到小车目标位置的Kalman滤波方程
4.Matlab仿真
例子5:Matlab kalman函数的使用
附录
1.使用Matlab中的Kalman函数
例子1.普遍文章里温度的例子
目的:估算k时刻的实际温度值
输入:k-1时刻的温度值,预测模型的误差方差,测量模型的误差方差。
计算过程:
(1)预测模型和测量模型为:
状态变量为温度值X,预测模型认为k时刻会延续k-1时刻的温度值,方差为w;测量值也为温度,所以和状态变量的关系为H=1,方差为v。
(2)假设k-1时刻的温度为23度,预测标准差为5度。测量得到k时刻的温度为25度,测量标准差为4度。
(3)方程的系数为A=1;B=0;H=1,5个核心公式如下:
其中:Q=5,R=4.
所以,k时刻时候:
X(k|k-1)=23;
P(k|k-1)=5*5;
Kg(k)=5*5/(5*5+4*4)=0.78;(错了,后面修改)
X(k|k)=23+0.78*[25-23]=24.56.
P(k|k)=[1-0.78]*25=5.5。
以上,k时刻的最优估计为24.56度。k时刻的最优值的方差为5.5。
例子2.论文中测距的例子
问题:在雷达定位时,目标位置不变,获得多次目标的距离值Ri,真实距离值恒定不变,在测量过程中真实值受到加性噪声n(k)的干扰,任意两个不同时刻的噪声互不相关。
(1)系统的预测模型和测量模型为
状态变量为距离值X,预测模型认为k时刻会延续k-1时刻的距离值,方差为0;测量值也为距离值,所以和状态变量的关系为H=1,方差为n(k)。
(2)方程的系数为
A=1,B=0,H=1,Q=0.5个核心公式如下
例子3.观测函数为y=5x
Matlab程序如下:
clc;clear;clf
%% 系统模型
%% 观测模型
% 观测值其实就是真实值+噪声
% observed_value=true_value+noise;
% 加入噪声 y=o*randn(M,N)+u;
x=1:1000;
y=5*x;
y1=y+50*randn(1,1000)+0;
%y1=y+wgn(1,1000,20);
true_value=y;
observed_value=y1;
%% 初始化
x_pre2pre=1;%初始最优估计值
p_pre2pre=0;%初始最小均方误差
Q=5*5;%过程噪声方差
R=50*50;%测量噪声方差
N=1000;
predict_value=zeros(1,N);%存储预测数据
y_now=y1;
%% 卡尔曼滤波
%卡尔曼公式
for i=1:1000
x_pre2now=x_pre2pre+5;
p_pre2now=p_pre2pre+Q;
Kg_now=(p_pre2now)/(p_pre2now+R);
x_now2now=x_pre2now+Kg_now*(y_now(i)-x_pre2now);
p_now2now=(1-Kg_now)*p_pre2now;
x_pre2pre=x_now2now;
p_pre2pre=p_now2now;
predict_value(i)=x_now2now;
end
%% 可视化
plot(true_value,'r');
hold on;
plot(observed_value,'g');
plot(predict_value,'b');
例子4:小车做匀速直线运动
1. 首先建立小车的状态转移模型
先考虑最简单的单x轴情况:由于小车做匀速直线运动,因此其加速度为0。但由于过程噪声的存在,就认为加速度存在一个高斯白噪声。
由牛顿运动定律可知:
定义状态变量X为:
则小车的状态转移模型可以表示如下:
由此可知对于二维平面的小车运动,小车的状态转移模型可以表示如下:
2.然后建立小车的观测模型
有一个两坐标雷达对该目标进行覆盖,由于测量值就是小车的状态变量X,因此:
v是测量噪声,也是高斯白噪声。
3.得到小车目标位置的Kalman滤波方程
由前面第1和2小节,可知:
过程噪声w的方差为,测量噪声的方差为
,由此更新Q和R为:
标准的Kalman公式如下:
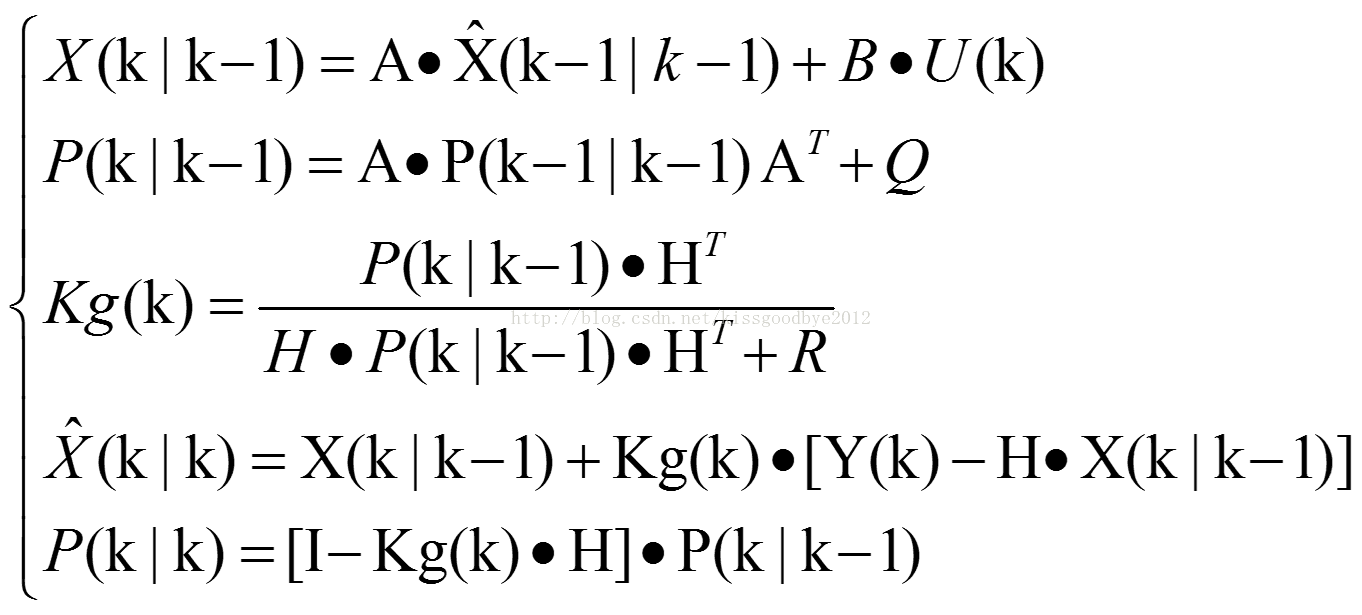
4.Matlab仿真
首先,初始化数值:
例子5:Matlab kalman函数的使用
1.前言
% kalman滤波函数
% 输入参数:QN为状态噪声的方差阵;RN为观测噪声的方差阵;NN表示状态噪声和观测噪声的协方差阵;
% 输出参数:KEST为系统输出估计值y和状态估计值x;L和M分别表示两个增益矩阵;P和Z分别代表预报误差方差阵和滤波误差方差阵
[KEST,L,P,M,Z]=kalman(SYS,QN,RN,NN)
——————————————————————————————————————————————————————
对于线性系统:
调用格式为:
[KEST,L,P,M,Z]=kalman(SYS,QN,RN,NN)
2.问题定义
已知离散系统
e和v是互不相关的高斯白噪声。假设x的初始值为,由此用Kalman滤波对数据进行仿真。
3.可运行代码
%%%%%%%系统描述
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% x[n+1]=Ax[n]+Bu[n]+Gw[n]
% y[n]=Cx[n]+Du[n]+Hw[n]+v[n]
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% 状态转移矩阵
A=[0.49 0.298 0.412
0.401 -0.391 0.391
-0.992 0.401 0.296];
% B矩阵
B=zeros(3,3);
% G矩阵
G=eye(3,3);
% C矩阵 向量
C=[0 1 0];
D=[0 0 0];
H=zeros(1,3);
% 状态向量初值(真值)
x(:,1)=[10.9 8.481 -4.3]';
% 状态向量初始估计值,不准也没关系,随着迭代会趋向于真值
guji=[10.1 11.3 10.7]';
% 进入循环
for i=2:30
%c产生 正态分布数据 y=o*randn(M,N)+u;返回一个均值为u,标准差为o的m*n的随机项矩阵
w=randn(3,1);
v=randn(1,1);
%真实数据
x(:,i)=A*x(:,i-1);
%人为制造系统误差
x1(:,i)=x(:,i)+w;
Qn=eye(2,2);
Rn=1;
Nn=0;
%人为制造观测数据的误差
z0(:,i)=C*x1(:,i)+v;
%建立Kalman的系统参数
sys=ss(A,[B,G],C,[D,H],-1);
[kest,L,P,M,Z]=kalman(sys,Qn,Rn,Nn);
%得到估计数据
guji(:,i)=A*guji(:,i-1)+L*(z0(:,i)-C*A*guji(:,i-1));
end
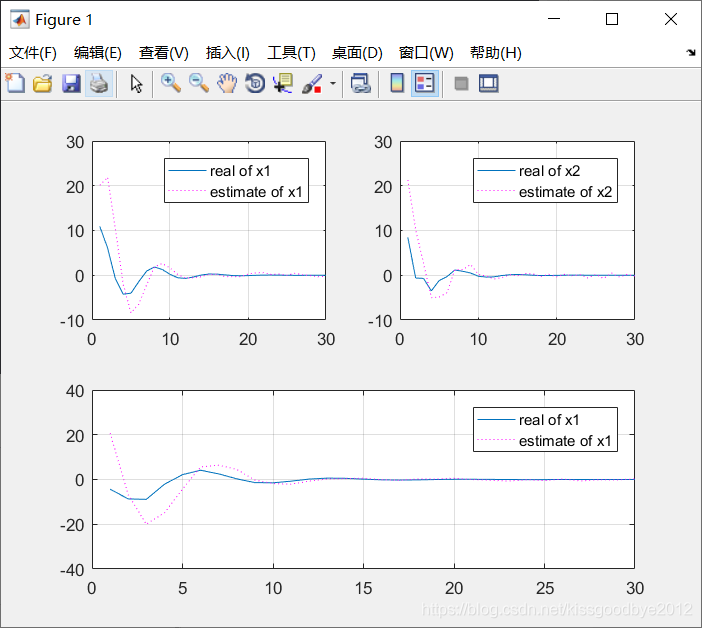
%% 结果展示,由于状态变量有3个,因此画了3幅图
subplot(2,2,1)
% 做出真值曲线 x1
plot(x(1,:))
hold on
% 做出在噪声污染情况下的滤波估计值曲线 x1
plot(guji(1,:),':m')
hold off
legend('real of x1','estimate of x1')
grid
subplot(2,2,2)
% 做出真值曲线 x2
plot(x(2,:))
hold on
% 做出在噪声污染情况下的滤波估计值曲线 x2
plot(guji(2,:),':m')
hold off
legend('real of x2','estimate of x2')
grid
subplot(2,2,3:4)
% 做出真值曲线 x3
plot(x(3,:))
hold on
% 做出在噪声污染情况下的滤波估计值曲线 x3
plot(guji(3,:),':m')
hold off
legend('real of x1','estimate of x1')
grid 4.仿真结果图
附录
1.使用Matlab中的Kalman函数
官方的例程路径如下:
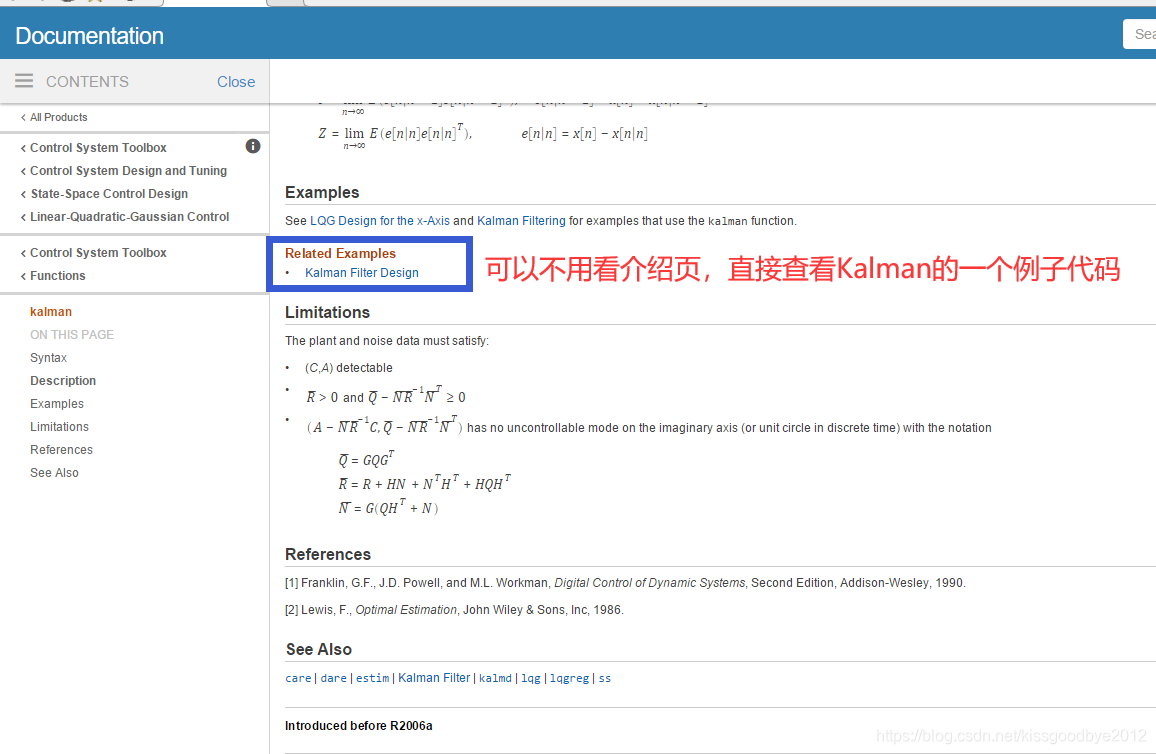
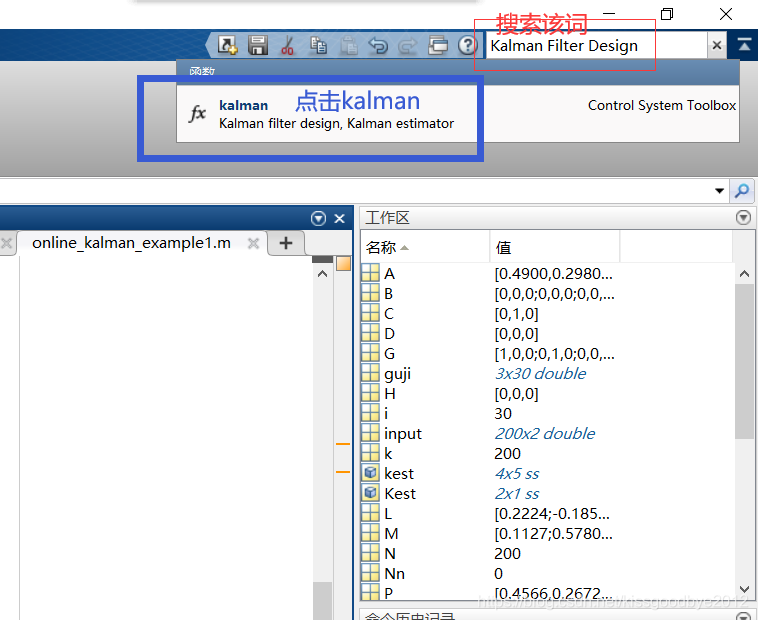
首先,在Matlab搜索栏搜索Kalman Filter Design,点击出现的kalman,进入Kalman函数介绍页面。如下图所示。
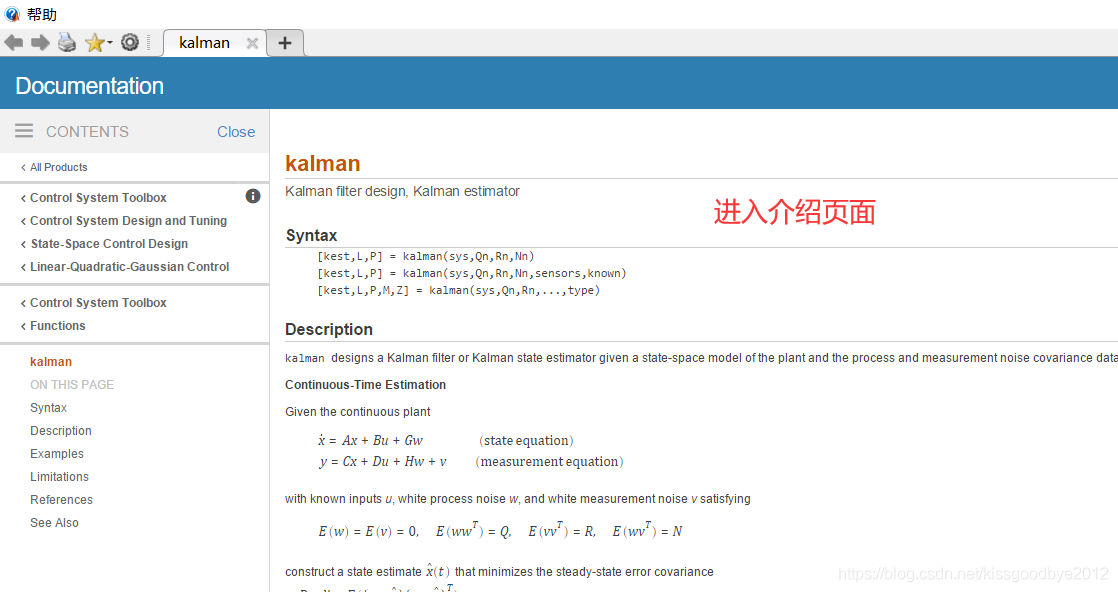
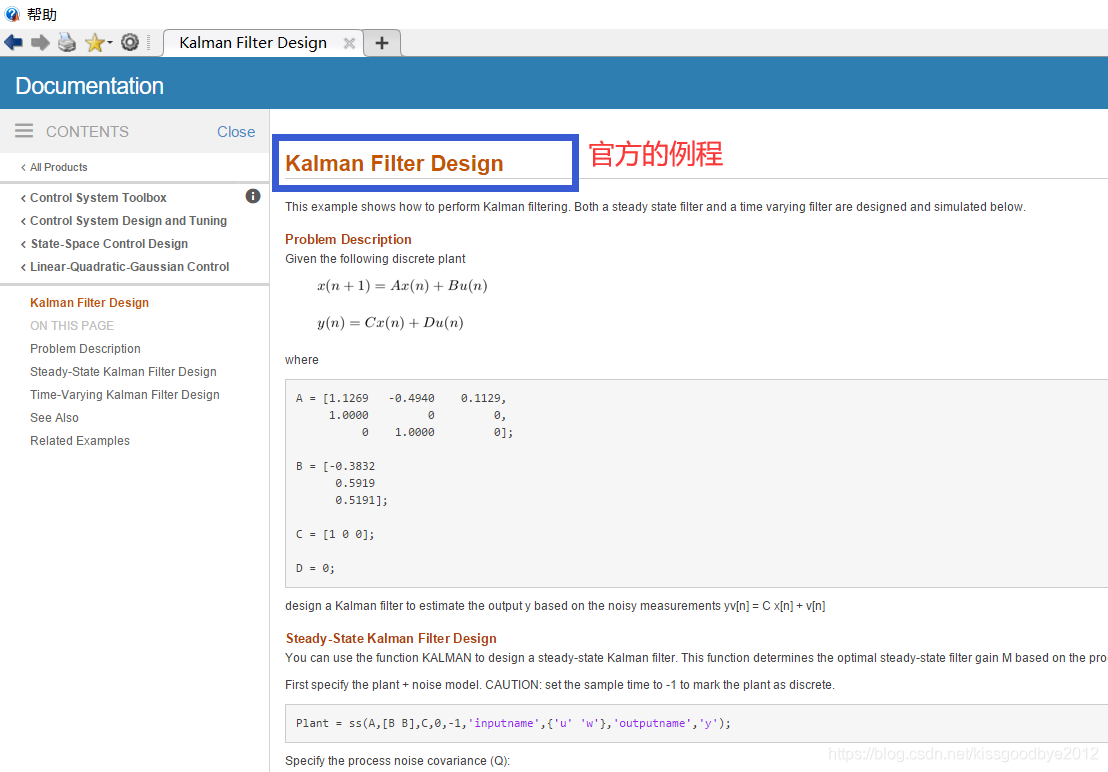
然后,滚动页面找到Example小节,点击Kalman Filter Design进入官方例程,如下图所示。