位置描述:一旦建立了坐标系,就可以用一个3×1的位置矢量对世界坐标系中的任何点进行定位。因为在世界坐标系中还有其他坐标系,因此必须在位置矢量上附加信息,表明是在哪个坐标被定义的。位置矢量用一个前置的上标来表明其参考坐标系。例如:AP。表明AP的数值是在坐标系{A}中的表示。矢量中的各个元素用下标x,y,z来表明:
姿态描述:点的位置描述可用矢量描述,姿态可用固定在物体上的坐标系来描述。描述连体坐标系{B}的一种方法是利用坐标系{A}的三个主轴单位矢量来表示。我们用 来表示坐标系{B}主轴方向的单位矢量,当用坐标系{A}的坐标表达式时,它们被写成
来表示坐标系{B}主轴方向的单位矢量,当用坐标系{A}的坐标表达式时,它们被写成 ,将这三个单位矢量按照顺序排成一个3×3的矩阵,称该矩阵为旋转矩阵,记作:
,将这三个单位矢量按照顺序排成一个3×3的矩阵,称该矩阵为旋转矩阵,记作: (矩阵{B}相对于矩阵{A}的表达)
(矩阵{B}相对于矩阵{A}的表达)

于是,点的位置可用一个矢量来表示,物体的姿态可用一个矩阵来表示,上式中rij可用每个矢量在其参考坐标系中的单位方向上投影的分量来表示。于是 的各个分量可用一对单位矢量的点积来表示:
的各个分量可用一对单位矢量的点积来表示:

为简单起见,上式最右边矩阵内的前置上标被省略了。由于两个单位矢量的点积可得到二者之间夹角的余弦,因此旋转矩阵的各分量常被称作方向余弦。
观察式(2)第一行可知:矩阵 的第一行就是
的第一行就是![]() 在
在 上的投影的模,也就是
上的投影的模,也就是![]() ,则,
,则,

坐标系{A}对坐标系{B}的描述![]() 可由式(3)转置得到;即,
可由式(3)转置得到;即,![]() ,又因为旋转矩阵是正交矩阵,一个正交矩阵的逆等于它的转置,因此,
,又因为旋转矩阵是正交矩阵,一个正交矩阵的逆等于它的转置,因此,![]() 现在以三个欧拉角中的RotX为例(其余两个欧拉角以此类推),验证一下以上说的结论。
现在以三个欧拉角中的RotX为例(其余两个欧拉角以此类推),验证一下以上说的结论。
(1)由于X轴是垂直于YoZ平面的,所以![]() 和
和![]() 的点乘结果为0,同时
的点乘结果为0,同时![]() 和
和![]() 的点乘结果也为0。
的点乘结果也为0。
(2)由于![]() 都是单位向量,所以
都是单位向量,所以![]() 和
和![]() 的点乘结果为1。
的点乘结果为1。
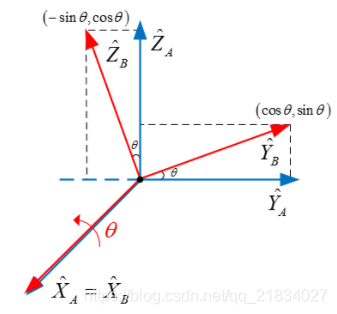
(3)由于绕x轴旋转,所以我们观察![]() 和
和![]() 分别在
分别在![]() 和
和![]() 上的投影情况,如下图所示。
上的投影情况,如下图所示。

坐标系描述:位置和姿态的组合称作坐标系,四个矢量为一组,表示了位置和姿态信息。例如,用, 和
和![]() 来描述坐标系{B},其中
来描述坐标系{B},其中![]() 是确定坐标系{B}原点位置矢量:{B}=
是确定坐标系{B}原点位置矢量:{B}=![]()
映射:坐标系到坐标系的变换:已知矢量对某坐标系{B}的描述,求出它相对另一坐标系{A}的描述。![]() ,其中
,其中![]() 为4×4齐次变换矩阵。
为4×4齐次变换矩阵。




