本节主要目的是介绍图像增强的一些基本概念。来源于东北大学 魏颖教授的数字图像课程笔记。 本节要点 
直方图均衡
- 直方图的基本概念
将图像中像素亮度(灰度级别)看成是一个随机变量, 则其分布情况反映了图像的统计特性,这可用Probability Density Function (PDF)来刻画和描述,表现为灰度直方图(Histogram)。 灰度直方图是灰度级的函数,表示图像中具有某种灰度级的像素的个数,反映了图像中每种灰度出现的频率。 灰度直方图的横坐标是灰度级,纵坐标是该灰度级出现的频度,它是图像最基本的统计特征。 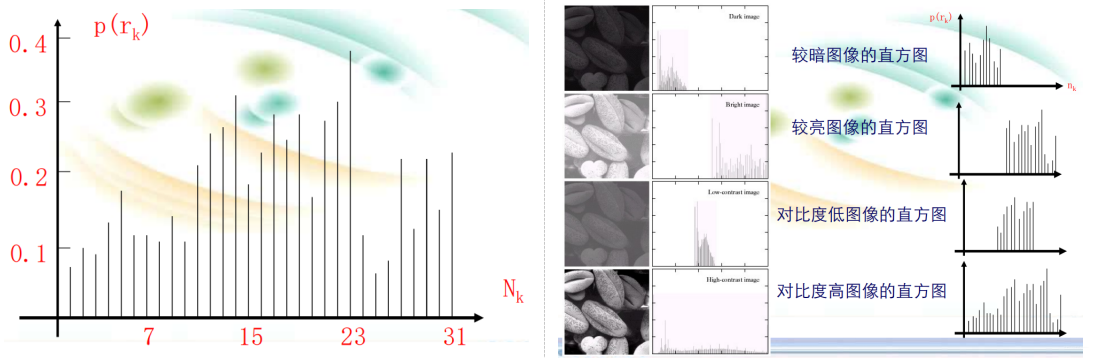
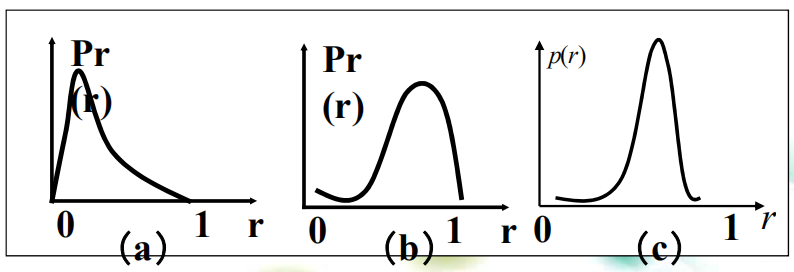 图(a)的大多数象素灰度值取在较暗的区域;图(b)图像的象素灰度值集中在亮区。图(c)图像的象素灰度值集中在某个较小的范围内,也就是说图像©的灰度集中在某一个小的亮区 直方图均衡化处理是以累积分布函数变换法为基础的直方图修正法。假定变换函数为
图(a)的大多数象素灰度值取在较暗的区域;图(b)图像的象素灰度值集中在亮区。图(c)图像的象素灰度值集中在某个较小的范围内,也就是说图像©的灰度集中在某一个小的亮区 直方图均衡化处理是以累积分布函数变换法为基础的直方图修正法。假定变换函数为  直方图均衡 直方图均衡化是将原图像的直方图通过变换函数修正为均匀的直方图,然后按均衡直方图修正原图像。 图像均衡化处理后,图像的直方图是平直的,即各灰度级具有相同的出现频数。
直方图均衡 直方图均衡化是将原图像的直方图通过变换函数修正为均匀的直方图,然后按均衡直方图修正原图像。 图像均衡化处理后,图像的直方图是平直的,即各灰度级具有相同的出现频数。 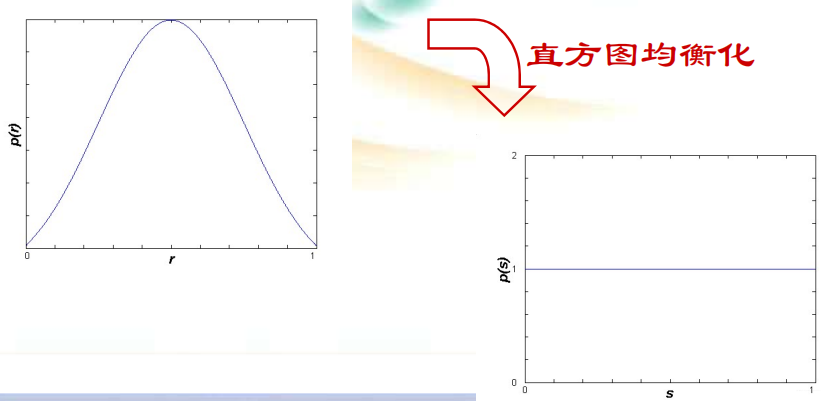 要找到一种变换 S=T(r)使直方图变平直,为使变换后的灰度仍保持从黑到白的单一变化顺序,避免整体变亮或变暗。规定: (1) :在0≤r≤1中,T(r)是单调递增函数,且0≤T(r)≤1;
要找到一种变换 S=T(r)使直方图变平直,为使变换后的灰度仍保持从黑到白的单一变化顺序,避免整体变亮或变暗。规定: (1) :在0≤r≤1中,T(r)是单调递增函数,且0≤T(r)≤1; 
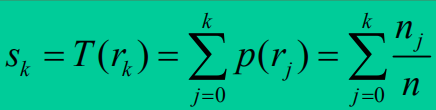 举例:设图象有64*64=4096个象素,有8个灰度级,灰度分布如表所示。进行直方图均衡化。
举例:设图象有64*64=4096个象素,有8个灰度级,灰度分布如表所示。进行直方图均衡化。  计算 sk
计算 sk  把计算的sk 就近安排到8个灰度级中。
把计算的sk 就近安排到8个灰度级中。 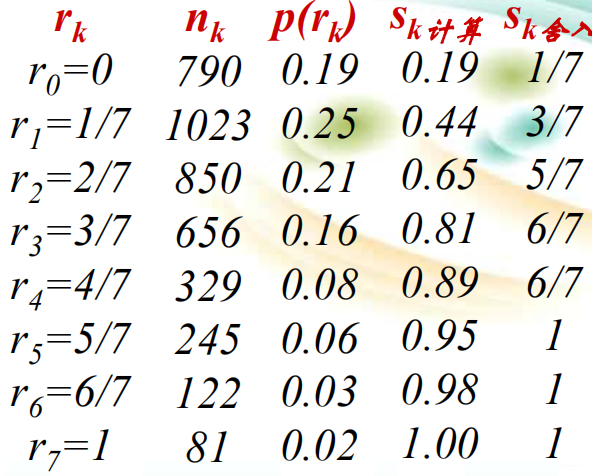 重新命名sk,归并相同灰度级的象素数。
重新命名sk,归并相同灰度级的象素数。 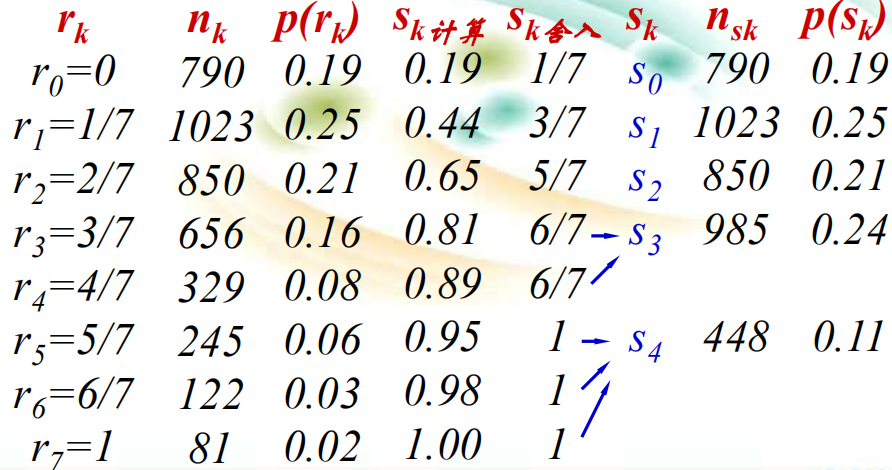 直方图均衡化实质上是减少图象的灰度级以换取对比度的加大。在均衡过程中,原来的直方图上频数较小的灰度级被归入很少几个或一个灰度级内,故得不到增强。若这些灰度级所构成的图象细节比较重要,则需采用局部区域直方图均衡。 直方图均衡化,力图使等长区间内出现的像素数接近相等。
直方图均衡化实质上是减少图象的灰度级以换取对比度的加大。在均衡过程中,原来的直方图上频数较小的灰度级被归入很少几个或一个灰度级内,故得不到增强。若这些灰度级所构成的图象细节比较重要,则需采用局部区域直方图均衡。 直方图均衡化,力图使等长区间内出现的像素数接近相等。 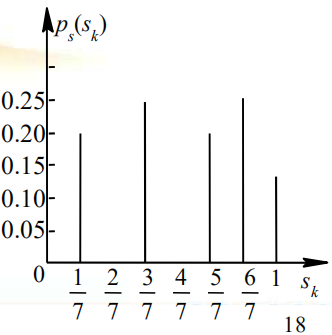
灰度变换
图像由像素组成,视觉效果与像素的灰度有关。从而可以通过改变像素灰度值来改变图像的视觉效果。灰度变换是一种点操作,赋予每个像素新的灰度值,关键在于设计变换函数(映射规则)。本节主要介绍三种灰度变换方法:线性灰度变换;分段线性变换;非线性变换。 1. 线性灰度变换 当图象成象时曝光不足或过度, 或由于成象设备的非线性和图象记录设备动态范围太窄等因素。都会产生对比度不足的弊病,使图象中的细节分辨不清。这时可将灰度范围线性扩展。 设f(x,y)灰度范围为[a,b],g(x,y)灰度范围[c,d]。 假定原图像f(x,y)的灰度范围为[a,b],希望变换后图像g(x,y)的灰度范围扩展至[c,d],则线性变换可表示为: 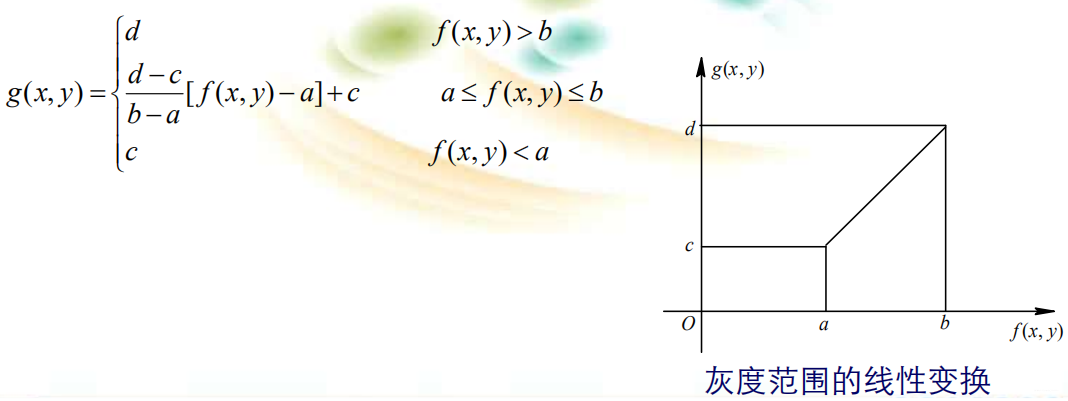 2. 分段线性变换 为了突出感兴趣的目标或灰度区间,相对抑制不感兴趣的灰度区域,可采用分段线性变换。常用的三段线性变换法数学表达式如下:
2. 分段线性变换 为了突出感兴趣的目标或灰度区间,相对抑制不感兴趣的灰度区域,可采用分段线性变换。常用的三段线性变换法数学表达式如下: 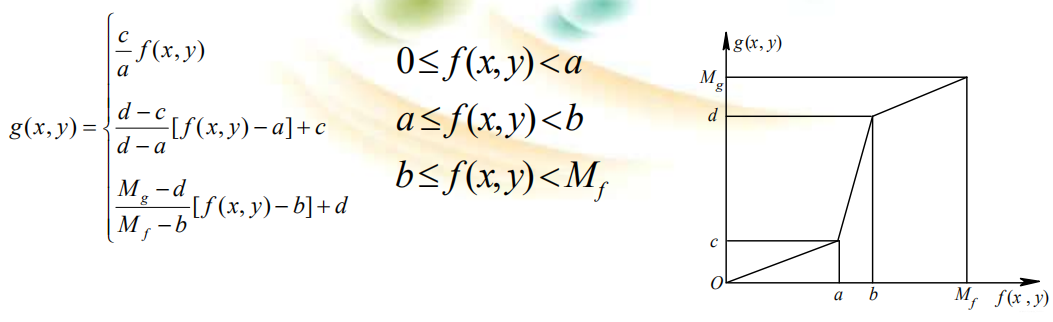 3. 非线性变换 非线性灰度变换主要有两种,对数变换和指数变换。对数变换将低灰度区扩展,高灰度区压缩;高灰度区扩展,低灰度区压缩。 对数变换:
3. 非线性变换 非线性灰度变换主要有两种,对数变换和指数变换。对数变换将低灰度区扩展,高灰度区压缩;高灰度区扩展,低灰度区压缩。 对数变换:  指数变换:
指数变换:  非线性变换:
非线性变换: 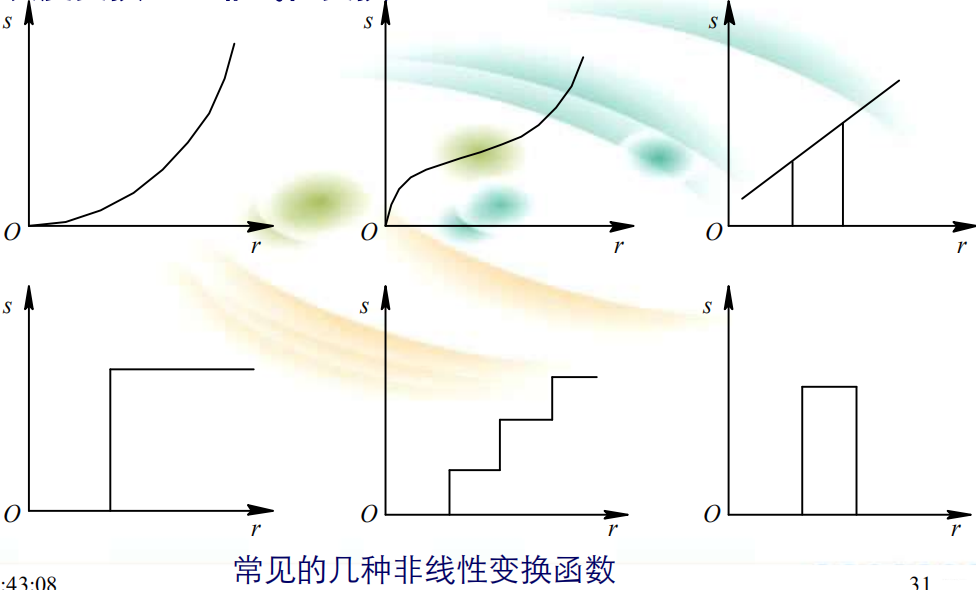
空间域滤波增强
噪声可以理解为“妨碍人们感觉器官对所接收的信源信息理解的因素”。例如,一幅黑白图像,其亮度分布假定为f(x,y), 那么对其起干扰作用的亮度分布R(x,y)便称为图像噪声。 噪声在理论上可以定义为“不可预测, 只能用概率统计方法来认识的随机误差”。将图像噪声看成是多维随机过程是合适的,描述噪声的方法完全可以借用随机过程及其概率分布函数和概率密度函数。 但在很多情况下,这种描述方法很复杂,甚至不可能,而且实际应用往往也不必要,通常是用其数字特征,即均值方差、相关函数等进行处理。
- 噪声分类
图像噪声按其产生的原因可分为外部噪声和内部噪声。外部噪声是指系统外部干扰从电磁波或经电源传进系统内部而引起的噪声,如电气设备、天体放电现像等引起的噪声。主要外部干扰如下: (1) 由光和电的基本性质所引起的噪声。 (2) 电器的机械运动产生的噪声。如, 各种接头因抖动引起的电流变化所产生的噪声;磁头、磁带抖动引起的抖动噪声等。 (3) 元器件材料本身引起的噪声。如, 磁带、 磁盘表面缺陷所产生的噪声 (4) 系统内部设备电路所引起的噪声。如, 电源系统引入的交流噪声,偏转系统和箝位电路引起的噪声等。 图像噪声从统计特性可分为平稳噪声和非平稳噪声两种。统计特性不随时间变化的噪声称为平稳噪声;统计特性随时间变化的噪声称为非平稳噪声。 另外,按噪声和信号之间的关系可分为加性噪声和乘性噪声。 假定信号为S(t),噪声为n(t),如果混合叠加波形是S(t)+n(t)形式,则称其为加性噪声;如果叠加波形为S(t)[1+n(t)]形式, 则称其为乘性噪声。 为了分析处理方便,往往将乘性噪声近似认为加性噪声,而且总是假定信号和噪声是互相独立的。
- 图像噪声的特点 1. 噪声在图像中的分布和大小不规则 2. 噪声与图像之间具有不相关性 3. 噪声具有叠加性
- 椒盐噪声和高斯噪声 常见的有椒盐噪声和高斯噪声
(1)高斯噪声: 高斯噪声是一种源于电子电路噪声和由低照明度或高温带来的传感器噪声。高斯噪声也常称为正态噪声,符合高斯分布。是自然界中最常见的噪声。高斯噪声可以通过空域滤波的平滑滤波方法来消除。  (2)椒盐噪声: 椒盐噪声又称双极脉冲噪声,其概率密度函数为:
(2)椒盐噪声: 椒盐噪声又称双极脉冲噪声,其概率密度函数为:  椒盐噪声是指图像中出现的噪声只有两种灰度值,分别为a和b,通常情况下脉冲噪声总是数字化为允许的最大或最小值,所以负脉冲以黑点(类似胡椒)出现在图像中,正脉冲以白点(类似盐)出现在图像中。
椒盐噪声是指图像中出现的噪声只有两种灰度值,分别为a和b,通常情况下脉冲噪声总是数字化为允许的最大或最小值,所以负脉冲以黑点(类似胡椒)出现在图像中,正脉冲以白点(类似盐)出现在图像中。  出现位置是随机的,但噪声的幅值是基本相同的。
出现位置是随机的,但噪声的幅值是基本相同的。  出现在位置是一定的(每一点上),但噪声的幅值是随机的。
出现在位置是一定的(每一点上),但噪声的幅值是随机的。
噪声的去除
改善降质图像的方法有两类:图像增强和图像复原 (1)图像增强:不考虑图像降质的原因, 只将图像中感兴趣的部分加以处理或突出有用的图像特征,故改善后的图像并不一定要去逼近原图像。主要目的是要提高图像的可懂度。(2)图像复原:针对图像降质的具体原因,设法补偿降质因素,使改善后的图像尽可能地逼近原始图像。 图像增强处理的方法基本上可分为空间域法和频域法两大类。 (1)空间域法 在原图像上直接进行数据运算,对像素的灰度值进行处理。它又分为两类:点运算和局部运算点运算:对图像作逐点运算局部运算:在与处理像点邻域有关的空间域上进行运算。 (2)频域法 在图像的变换域上进行处理, 增强感兴趣的频率分量, 然后进行反变换,得到增强了的图像。 
- 线性滤波器的定义
 主要线性空域滤波器:主要包括低通滤波器、高通滤波器、带通滤波器。低通滤波器主要用于:钝化图像、去除噪声;高通滤波器 主要用于边缘增强、边缘提取;带通滤波器主要用于删除特定频率。
主要线性空域滤波器:主要包括低通滤波器、高通滤波器、带通滤波器。低通滤波器主要用于:钝化图像、去除噪声;高通滤波器 主要用于边缘增强、边缘提取;带通滤波器主要用于删除特定频率。
- 非线性滤波器
非线性滤波器的定义:使用模板进行结果像素值的计算,结果值直接取决于像素邻域的值,而不使用乘积和的计算。主要非线性滤波器有:中值滤波、最大值滤波、最小值滤波。 
图像平滑
线性平滑滤波器:均值滤波器  空间平滑滤波器包括:平滑线性滤波器、统计排序非线性滤波器(中值滤波) 分别采用n=3,5,9,15,35像素的方形均值滤波器得到的平滑结果。 模板尺寸越大,图像越模糊,图像细节丢失越多 低通空域滤波的缺点和问题如果图像处理的目的是去除噪声,那么,线性平滑低通滤波在去除噪声的同时也钝化了边和尖锐的细节。 统计滤波器是非线性滤波:滤波器模板包围的图像区域中像素排序,统计排序结果代替中心像素的值;中值滤波器是应用最广泛的统计滤波器;中值滤波对一定类型的随机噪声(如椒盐噪声)提供了优秀的去噪能力,比小尺寸的线性平滑滤波器的模糊程度明显低。 中值滤波的原理 用模板区域内像素的中值,作为结果值R=mid{zk∣k=1,2,…,9};强迫突出的亮点(暗点)更象它周围的值,以消除孤立的亮点(暗点)
空间平滑滤波器包括:平滑线性滤波器、统计排序非线性滤波器(中值滤波) 分别采用n=3,5,9,15,35像素的方形均值滤波器得到的平滑结果。 模板尺寸越大,图像越模糊,图像细节丢失越多 低通空域滤波的缺点和问题如果图像处理的目的是去除噪声,那么,线性平滑低通滤波在去除噪声的同时也钝化了边和尖锐的细节。 统计滤波器是非线性滤波:滤波器模板包围的图像区域中像素排序,统计排序结果代替中心像素的值;中值滤波器是应用最广泛的统计滤波器;中值滤波对一定类型的随机噪声(如椒盐噪声)提供了优秀的去噪能力,比小尺寸的线性平滑滤波器的模糊程度明显低。 中值滤波的原理 用模板区域内像素的中值,作为结果值R=mid{zk∣k=1,2,…,9};强迫突出的亮点(暗点)更象它周围的值,以消除孤立的亮点(暗点)  中值滤波算法的实现
中值滤波算法的实现
- 将模板区域内的像素排序,求出中值。 例如: 3×3的模板,第5大的是中值, 5×5的模板,第13大的是中值, 7×7的模板,第25大的是中值, 9×9的模板,第41大的是中值。
- 对于同值像素,连续排列。如(10,15,20,20,20,20,20,25,100)
- 中值滤波算法的特点
在去除噪声的同时,可以比较好地保留边的锐度和图像的细节。对于椒盐噪声,中值滤波效果比均值滤波效果好;对于高斯噪声,均值滤波效果比中值滤波效果好。
- 最大值滤波和最小值滤波:
最大值滤波可以去除图像中的暗斑,同时也会使亮斑增大;最小值滤波可以去除图像中的亮斑 ,同时也会增大暗斑。 
图像锐化
- 基本概念
图像边缘是图像的基本特征之一,它包含对人类视觉和机器识别有价值的物体图像边缘信息。 边缘是图像中特性(如像素灰度、纹理等)分布的不连续处,图像周围特性有阶跃变化或屋脊状变化的那些像素集合。图像边缘存在于目标与背景、目标与目标、基元与基元的边界,它标示出目标物体或基元的实际含量,是图像识别信息最集中的地方。 图像锐化就是要突出图像边缘,抑制图像中非边缘信息,使图像轮廓更加清晰。由于边缘占据图像的高频成分,所以边缘增强通常属于高通滤波。 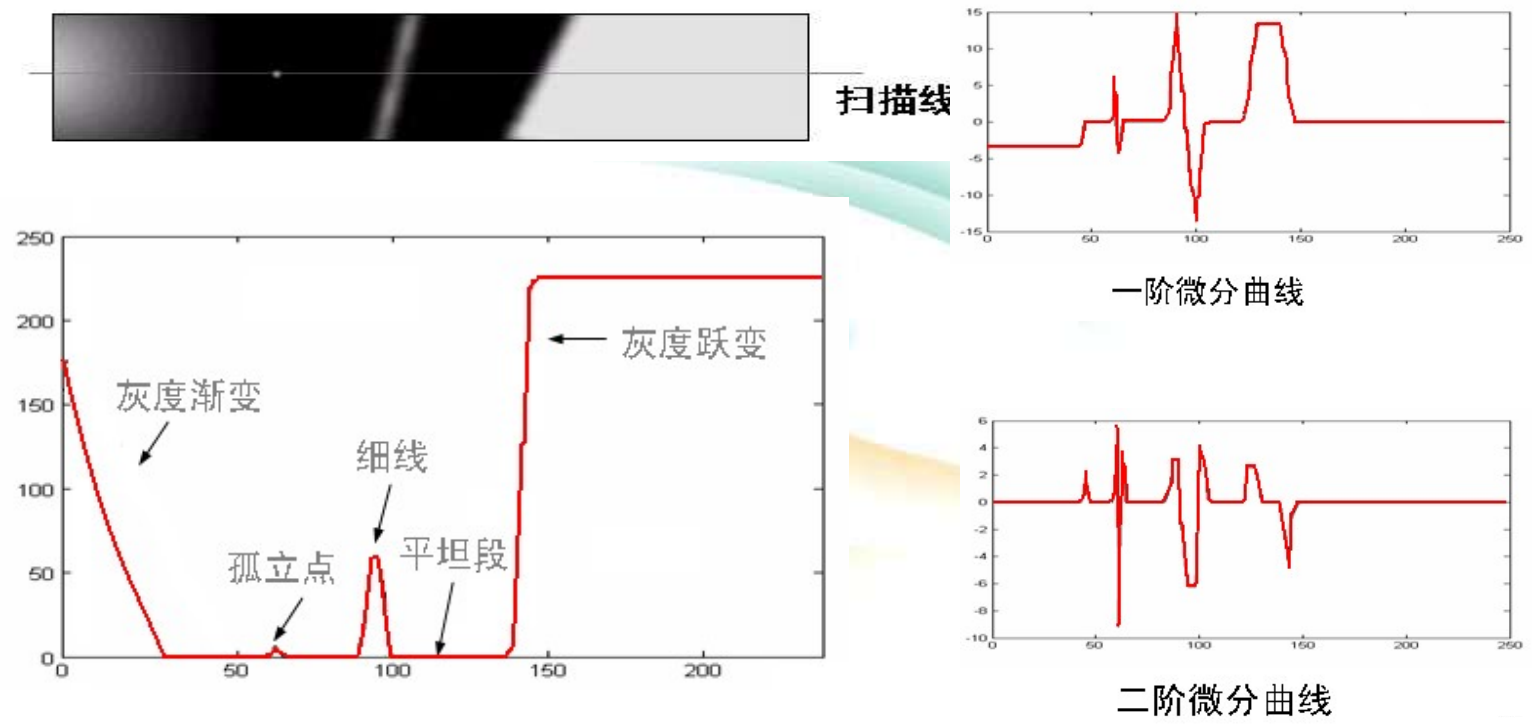
- 图像锐化及增强方法
这里介绍三个方法:(1) 基本高通滤波模板;(2) 高频补偿滤波;(3) 图像微分,包括:一阶微分—梯度法;二阶微分—拉普拉斯算子; (1) 基本高通滤波模板 我们先介绍高通滤波模板:图像锐化是要增强图像频谱中的高频部分,就相当于从原图像中减去它的低频分量,即原始图像经平滑处理后所得的图像。选择不同的平滑方法,会有不同的图像锐化结果。 
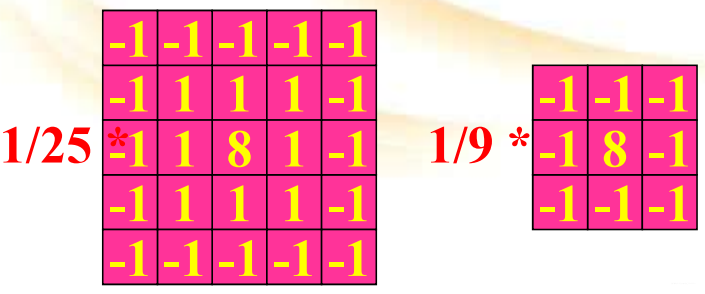 滤波器效果的分析: 常数或变化平缓的区域,结果为0或很小,图像很暗,亮度被降低了;在暗的背景上边缘被增强了;图像的整体对比度降低了;计算时会出现负值,归0处理为常见。 基本高通空域滤波的缺点和问题:高通滤波在增强了边的同时,丢失了图像的层次和亮度。 (2) 高频补偿滤波(提升滤波): 弥补高通滤波的缺陷,在增强边和细节的同时,不丢失原图像的低频成分。
滤波器效果的分析: 常数或变化平缓的区域,结果为0或很小,图像很暗,亮度被降低了;在暗的背景上边缘被增强了;图像的整体对比度降低了;计算时会出现负值,归0处理为常见。 基本高通空域滤波的缺点和问题:高通滤波在增强了边的同时,丢失了图像的层次和亮度。 (2) 高频补偿滤波(提升滤波): 弥补高通滤波的缺陷,在增强边和细节的同时,不丢失原图像的低频成分。  滤波器扩大因子及模板系数设计:
滤波器扩大因子及模板系数设计: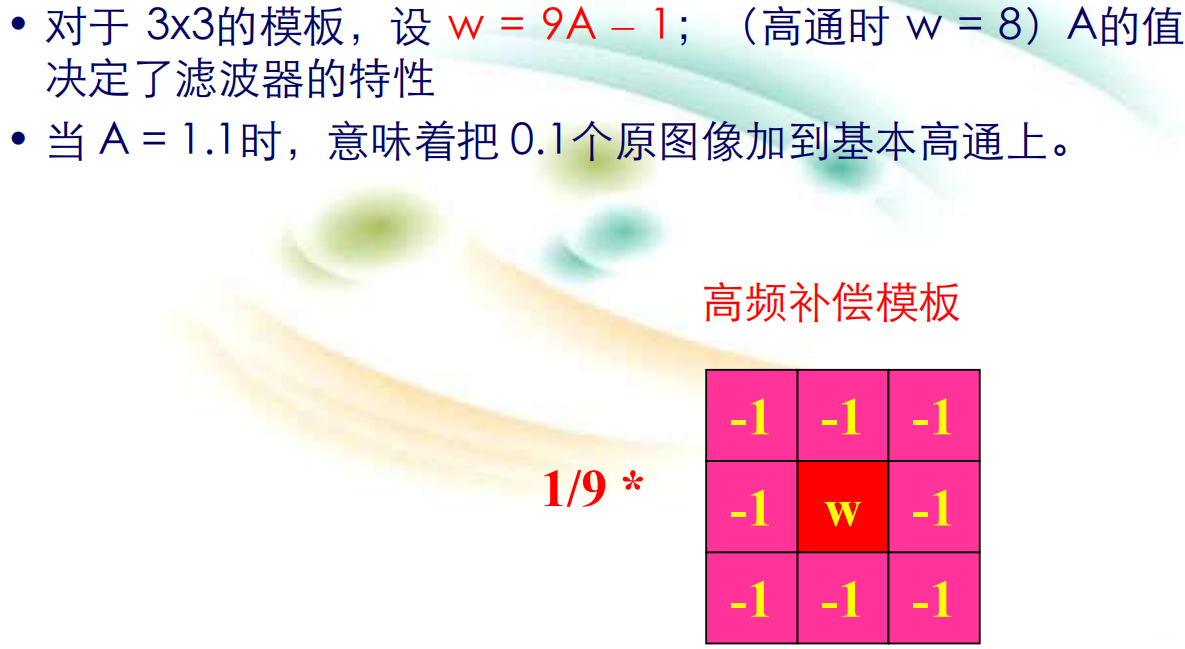 高频补偿滤波器效果的分析: 高频补偿比高通的优点是很明显的,即增强了边缘,又保留了层次。噪声对结果图像的视觉效果有重要的影响,高频补偿在增强了边的同时也增强了噪声。 (3) 图像微分 均值产生钝化的效果,而均值与积分相似,由此而联想到,微分能不能产生相反的效果,即锐化的效果呢?结论是肯定的。图像微分主要有一阶微分和二阶微分。
高频补偿滤波器效果的分析: 高频补偿比高通的优点是很明显的,即增强了边缘,又保留了层次。噪声对结果图像的视觉效果有重要的影响,高频补偿在增强了边的同时也增强了噪声。 (3) 图像微分 均值产生钝化的效果,而均值与积分相似,由此而联想到,微分能不能产生相反的效果,即锐化的效果呢?结论是肯定的。图像微分主要有一阶微分和二阶微分。  一阶微分(梯度法):
一阶微分(梯度法): 
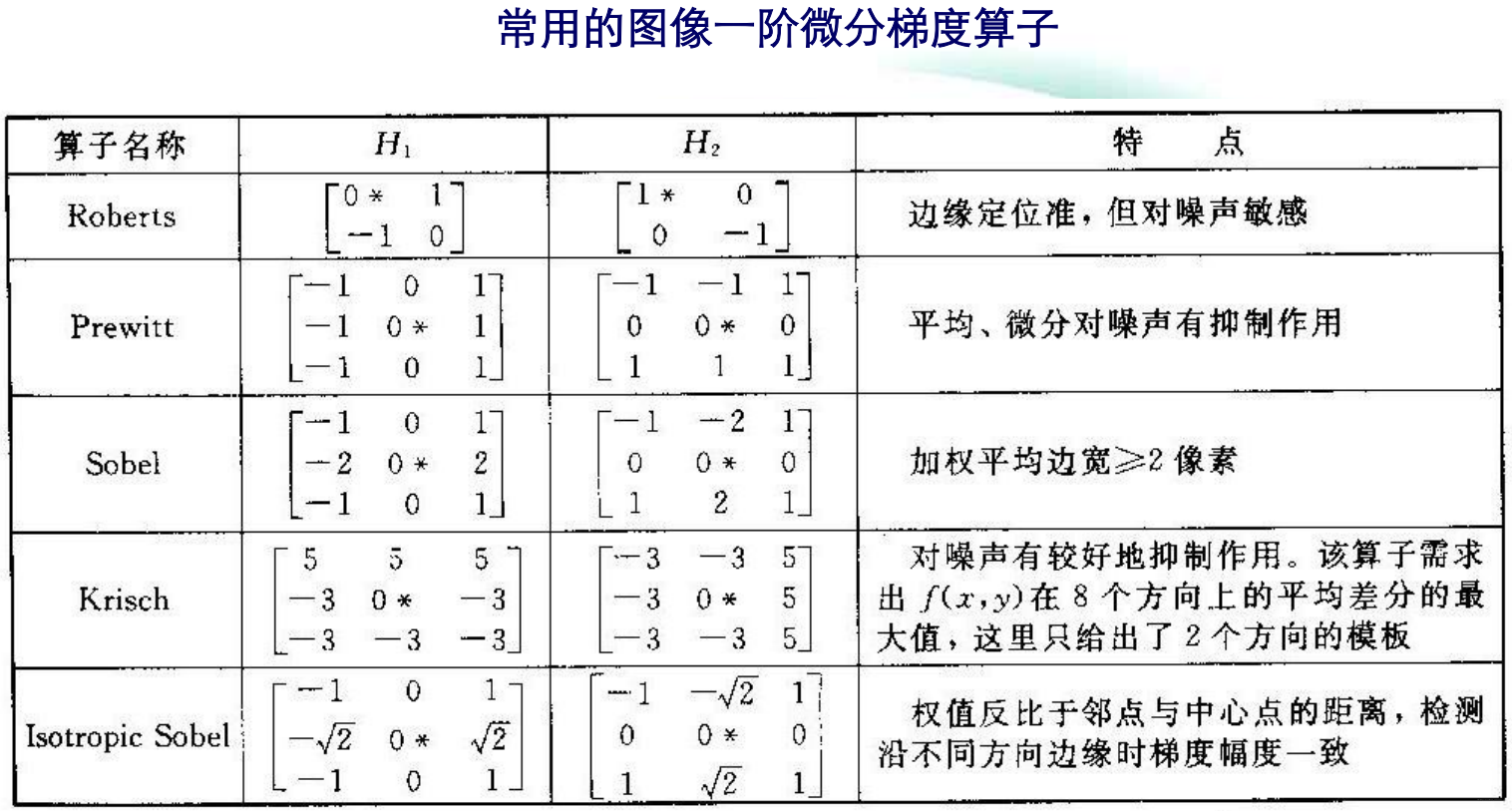
 介绍了一阶微分的大致原理,我们接下来介绍一下微分滤波器常用三种模板:Roberts交叉梯度算子;Prewitt梯度算子;Sobel梯度算子。 Roberts交叉梯度算子:
介绍了一阶微分的大致原理,我们接下来介绍一下微分滤波器常用三种模板:Roberts交叉梯度算子;Prewitt梯度算子;Sobel梯度算子。 Roberts交叉梯度算子: 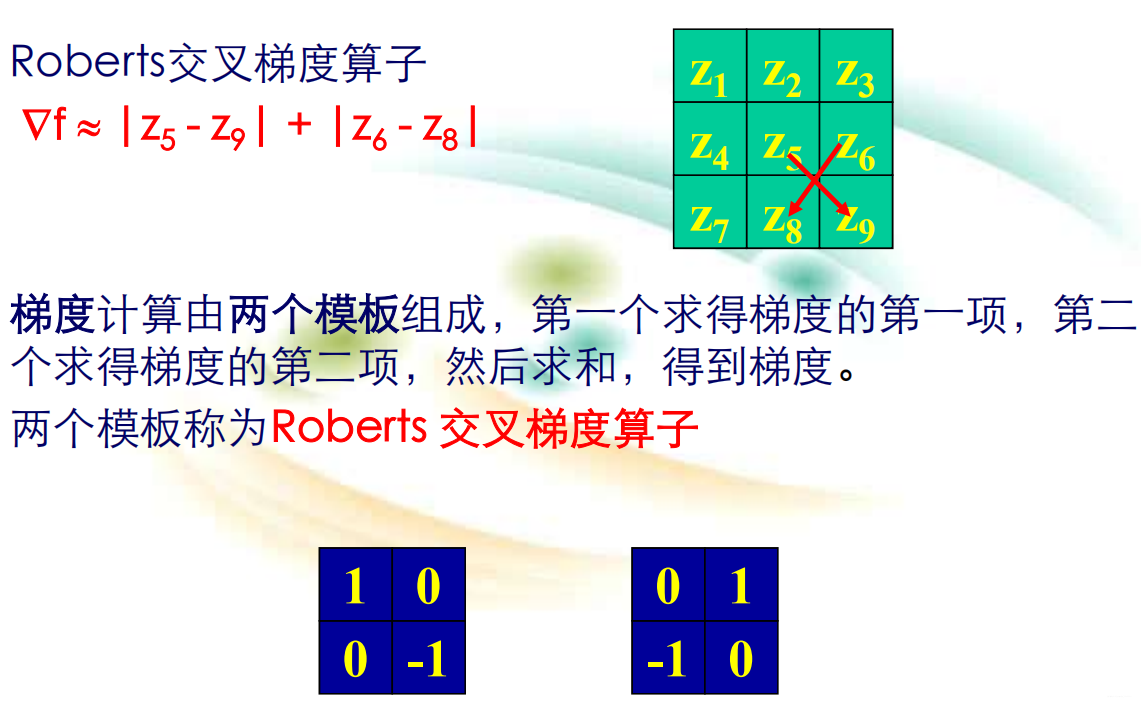 Prewitt梯度算子:
Prewitt梯度算子: Sobel算子: 采用梯度微分锐化图像,同时会使噪声、条纹等得到增强,Sobel算子则在一定程度上克服了这个问题。
Sobel算子: 采用梯度微分锐化图像,同时会使噪声、条纹等得到增强,Sobel算子则在一定程度上克服了这个问题。 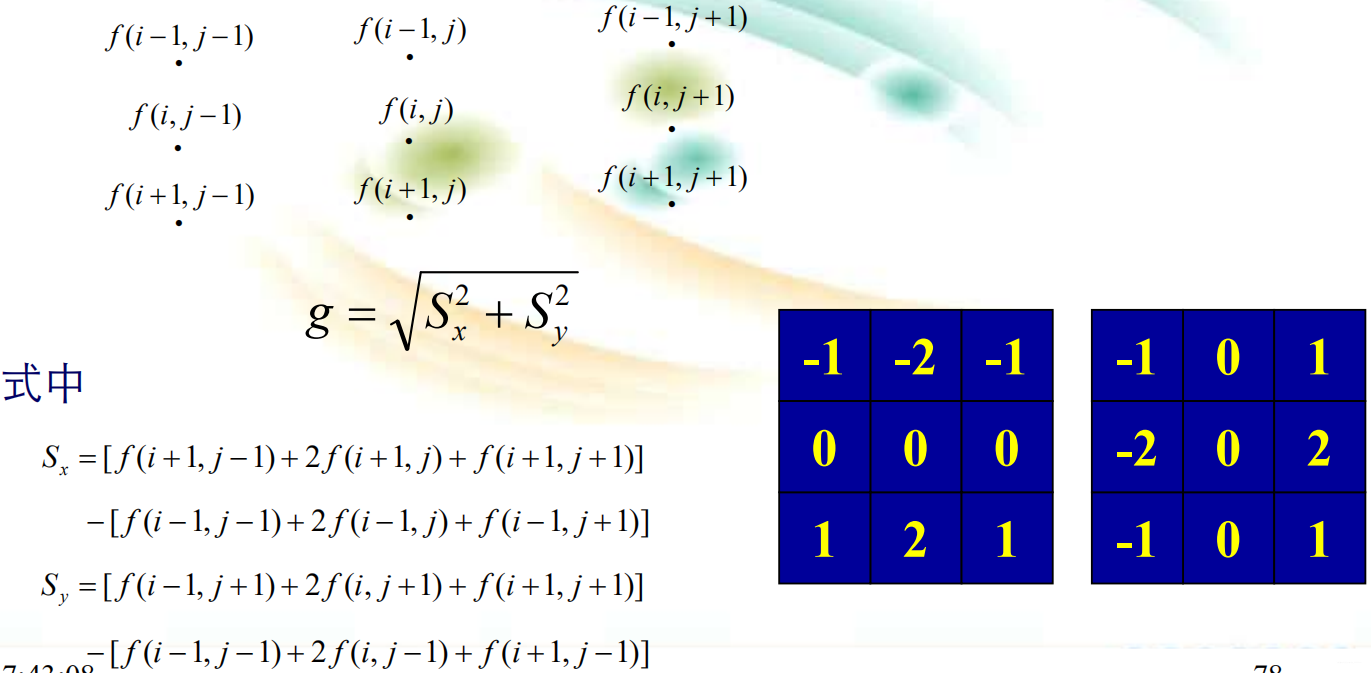

 二阶微分: 对数字图像来讲,f(x,y)的二阶偏导数可表示为:
二阶微分: 对数字图像来讲,f(x,y)的二阶偏导数可表示为: 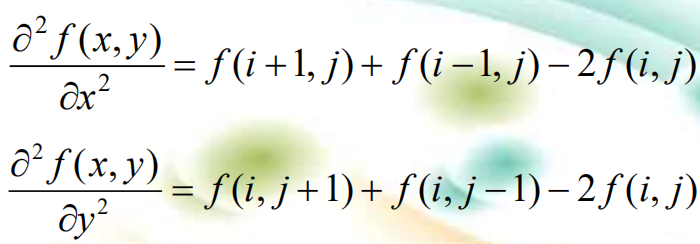 拉普拉斯算子是常用的边缘增强算子,拉普拉斯运算也是偏导数运算的线性组合运算,而且是一种**各向同性(旋转不变性)**的线性运算。拉普拉斯算子▽2f为:
拉普拉斯算子是常用的边缘增强算子,拉普拉斯运算也是偏导数运算的线性组合运算,而且是一种**各向同性(旋转不变性)**的线性运算。拉普拉斯算子▽2f为: 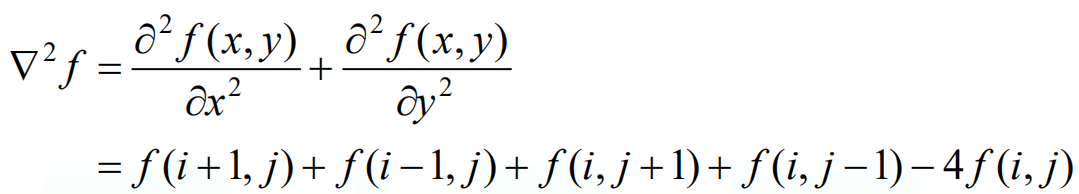 采用拉普拉斯算子对图像的增强的基本方法可表示为:
采用拉普拉斯算子对图像的增强的基本方法可表示为: 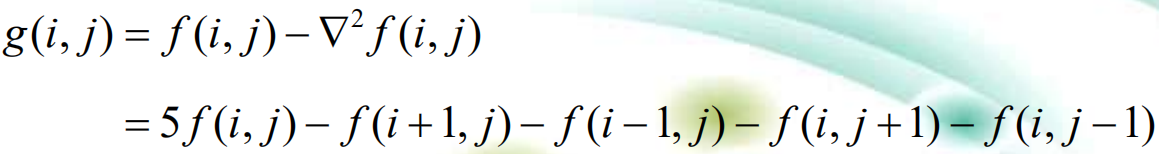 拉普拉斯算子:
拉普拉斯算子: 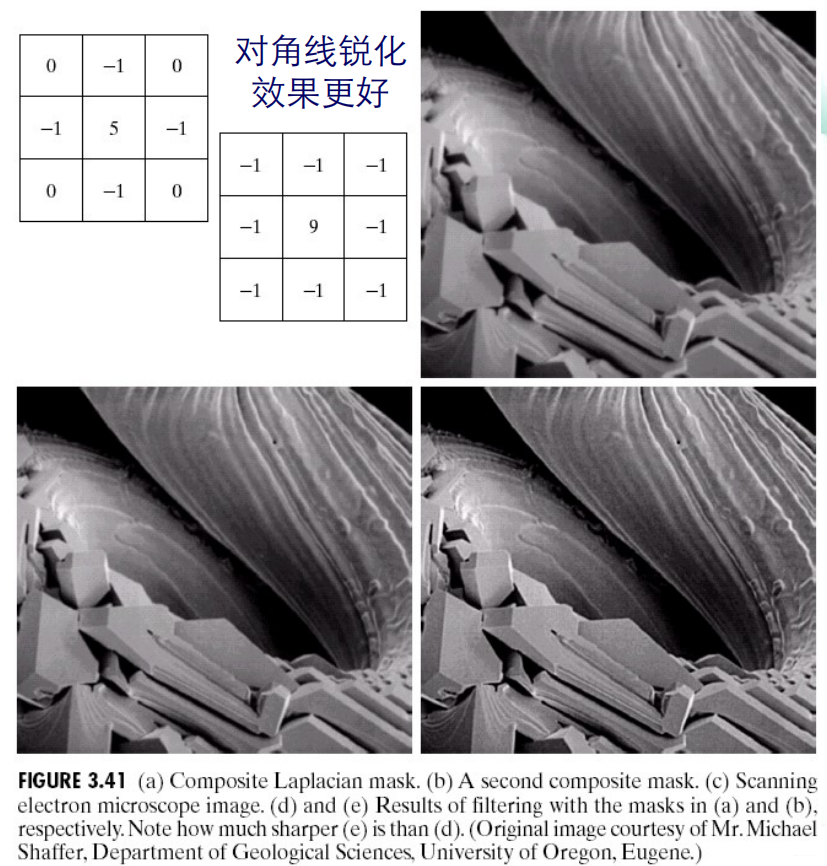
图像频域处理的理论基础
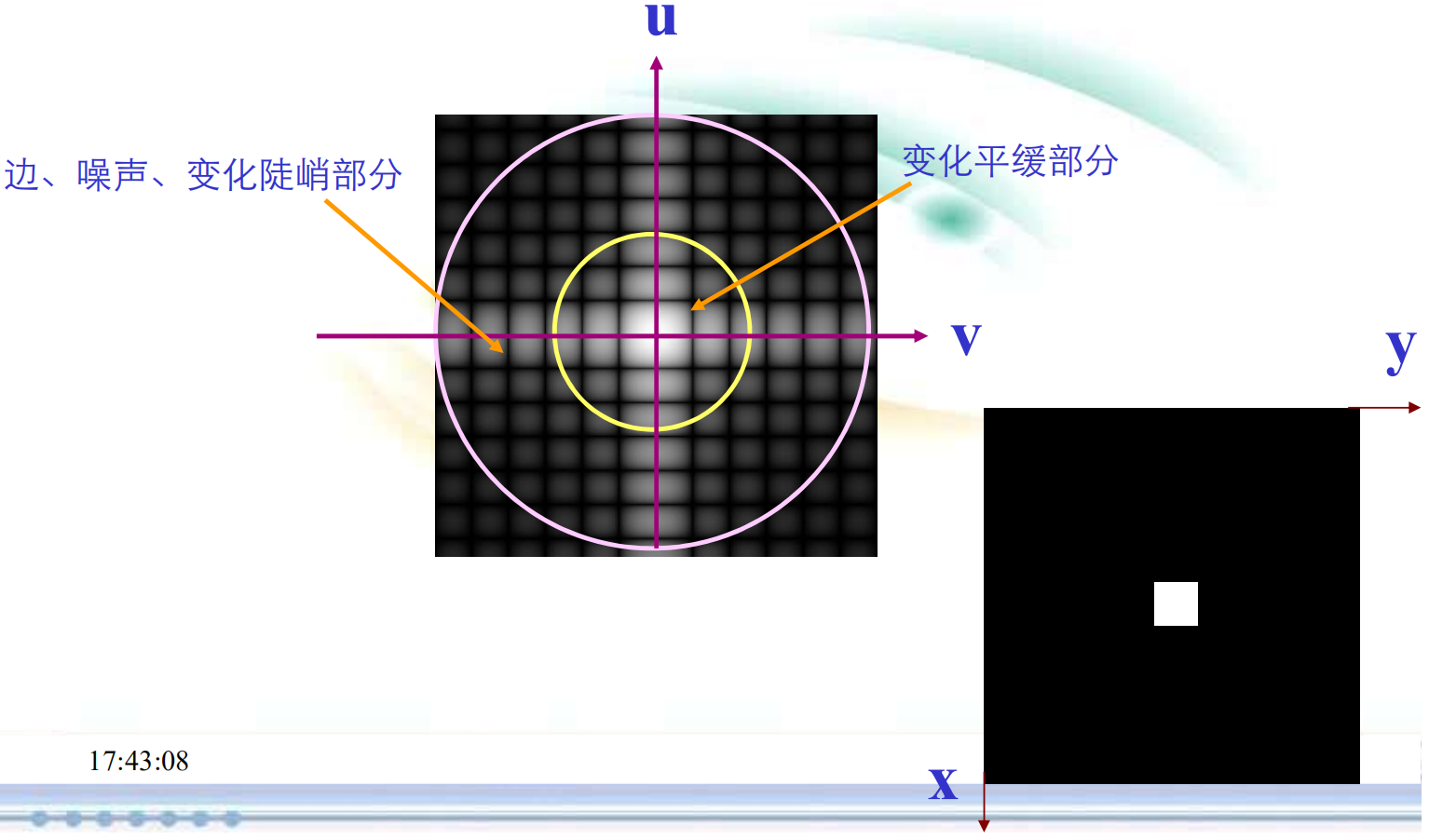
频率平面与图像空域特性的关系。 图像变化平缓的部分靠近频率平面的圆心,这个区域为低频区域;图像中的边、噪声、变化陡峻的部分,以放射方向离开频率平面的圆心,这个区域为高频区域。 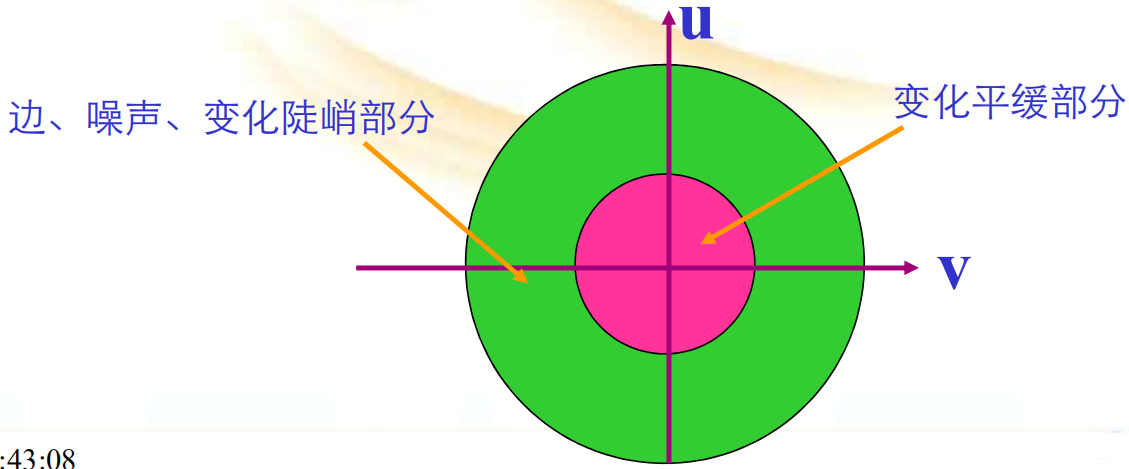
 图像频域的处理方法:通过傅立叶变换方法
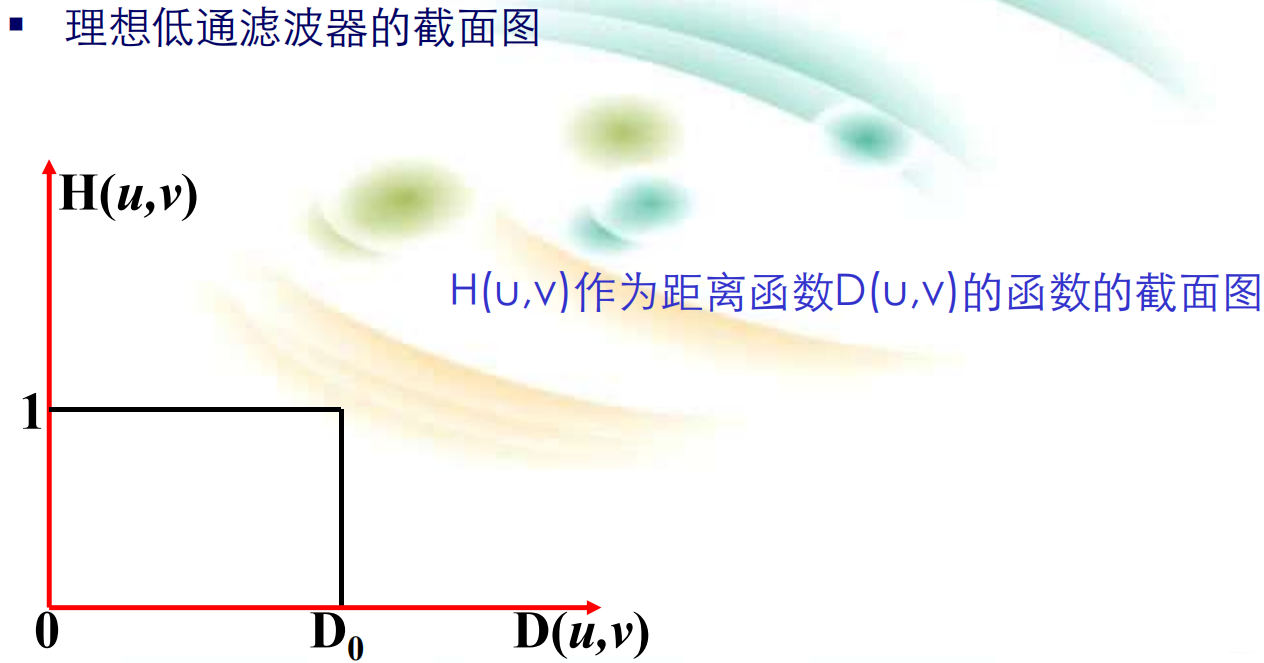
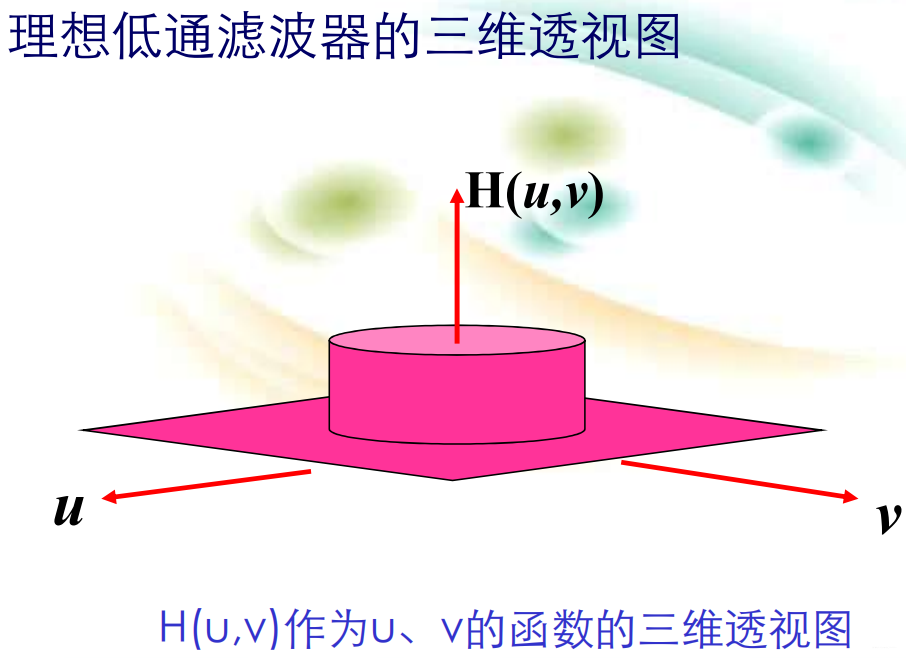
图像频域的处理方法:通过傅立叶变换方法  频域增强与空域增强的关系:1. 在实践中,小的空间模板比傅立叶变换用得多得多,因为它们易于实现。2. 对于很多在空域上难以表述清楚的问题,对频域概念的理解就显得十分重要。在图像压缩中更体会到。 这里我们介绍频域滤波器的三种滤波器:1)低通滤波;2)高通滤波;3)同态滤波。 (1)平滑(低通)滤波: 频域低通滤波的基本思想G(u,v)=F(u,v)H(u,v),F(u,v)是需要钝化图像的傅立叶变换形式,H(u,v)是选取的一个滤波器变换函数G(u,v)是通过H(u,v)减少F(u,v)的高频部分,来得到的结果运用傅立叶逆变换得到钝化后的图像。 理想低通滤波器的定义:
频域增强与空域增强的关系:1. 在实践中,小的空间模板比傅立叶变换用得多得多,因为它们易于实现。2. 对于很多在空域上难以表述清楚的问题,对频域概念的理解就显得十分重要。在图像压缩中更体会到。 这里我们介绍频域滤波器的三种滤波器:1)低通滤波;2)高通滤波;3)同态滤波。 (1)平滑(低通)滤波: 频域低通滤波的基本思想G(u,v)=F(u,v)H(u,v),F(u,v)是需要钝化图像的傅立叶变换形式,H(u,v)是选取的一个滤波器变换函数G(u,v)是通过H(u,v)减少F(u,v)的高频部分,来得到的结果运用傅立叶逆变换得到钝化后的图像。 理想低通滤波器的定义: 
 理想低通滤波器的截止频率的设计:
理想低通滤波器的截止频率的设计: 
 平滑(低通)滤波—理想低通滤波:
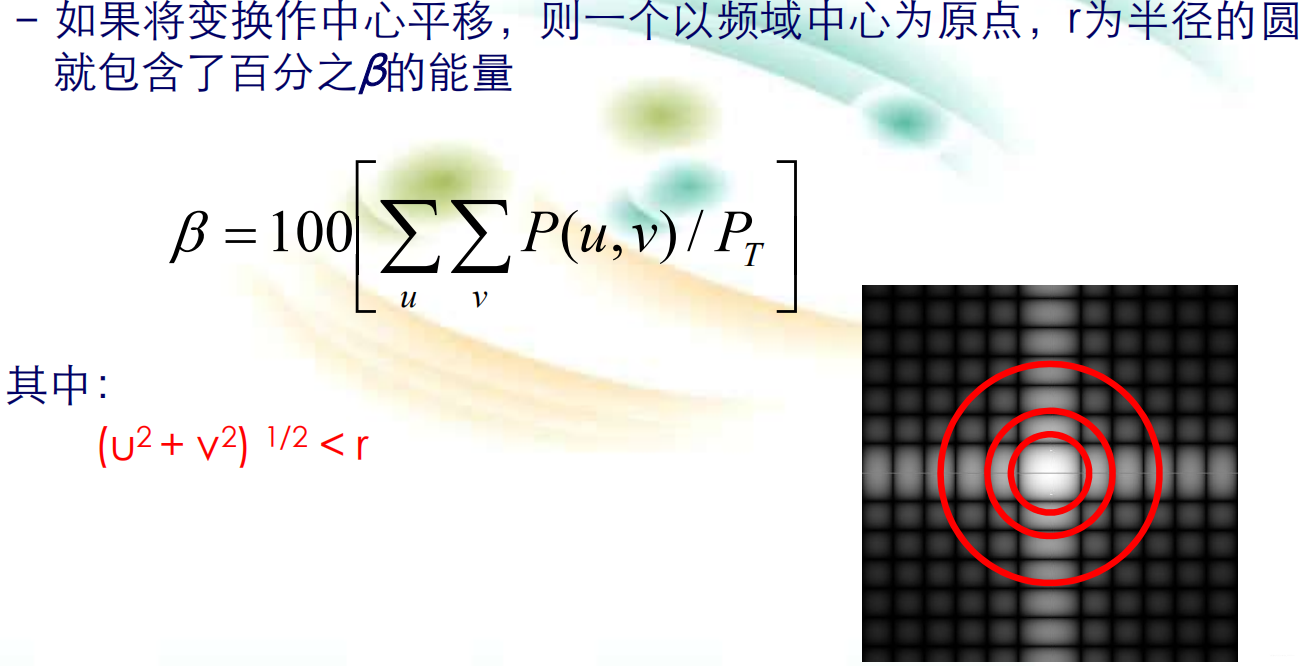
平滑(低通)滤波—理想低通滤波:  理想低通滤波器的分析: (1)整个能量的92%被一个半径为5的小圆周包含,大部分尖锐的细节信息都存在于被去掉的8%的能量中。(2)小的边界和其它尖锐细节信息被包含在频谱的至多0.5%的能量中。(3)被钝化的图像被一种非常严重的振铃效果——理想低通滤波器的一种特性所影响。 理想低通滤波器的平滑作用非常明显,但由于变换有一个陡峭的波形,它的反变换h(x,y)有强烈的振铃特性,使滤波后图像产生模糊效果。因此这种理想低通滤波实用中不能采用。
理想低通滤波器的分析: (1)整个能量的92%被一个半径为5的小圆周包含,大部分尖锐的细节信息都存在于被去掉的8%的能量中。(2)小的边界和其它尖锐细节信息被包含在频谱的至多0.5%的能量中。(3)被钝化的图像被一种非常严重的振铃效果——理想低通滤波器的一种特性所影响。 理想低通滤波器的平滑作用非常明显,但由于变换有一个陡峭的波形,它的反变换h(x,y)有强烈的振铃特性,使滤波后图像产生模糊效果。因此这种理想低通滤波实用中不能采用。 
- Butterworth低通滤波
Butterworth低通过滤器的定义: 一个截止频率在与原点距离为D 0 D_{0}D0的n阶Butterworth低通过滤器(BLPF)的变换函数如下: 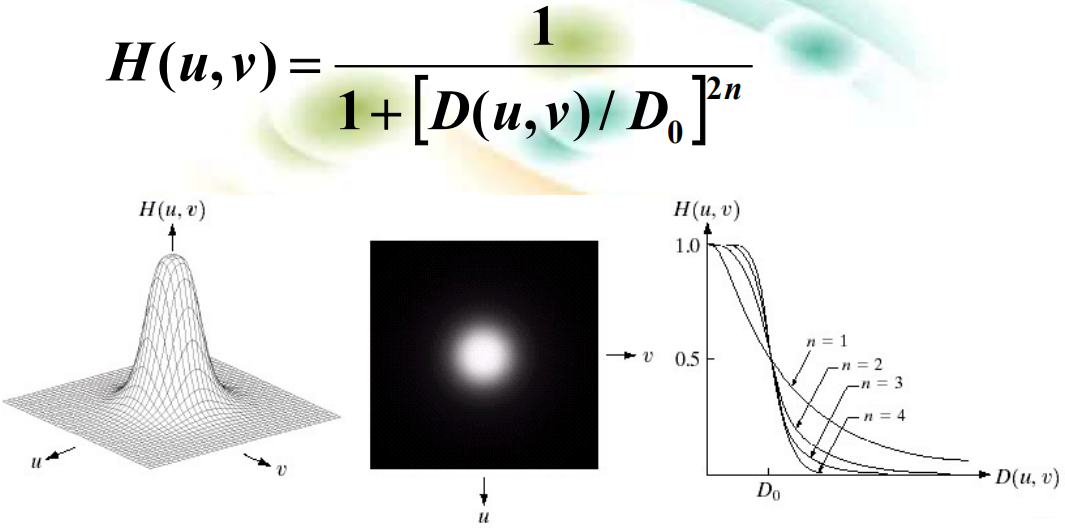
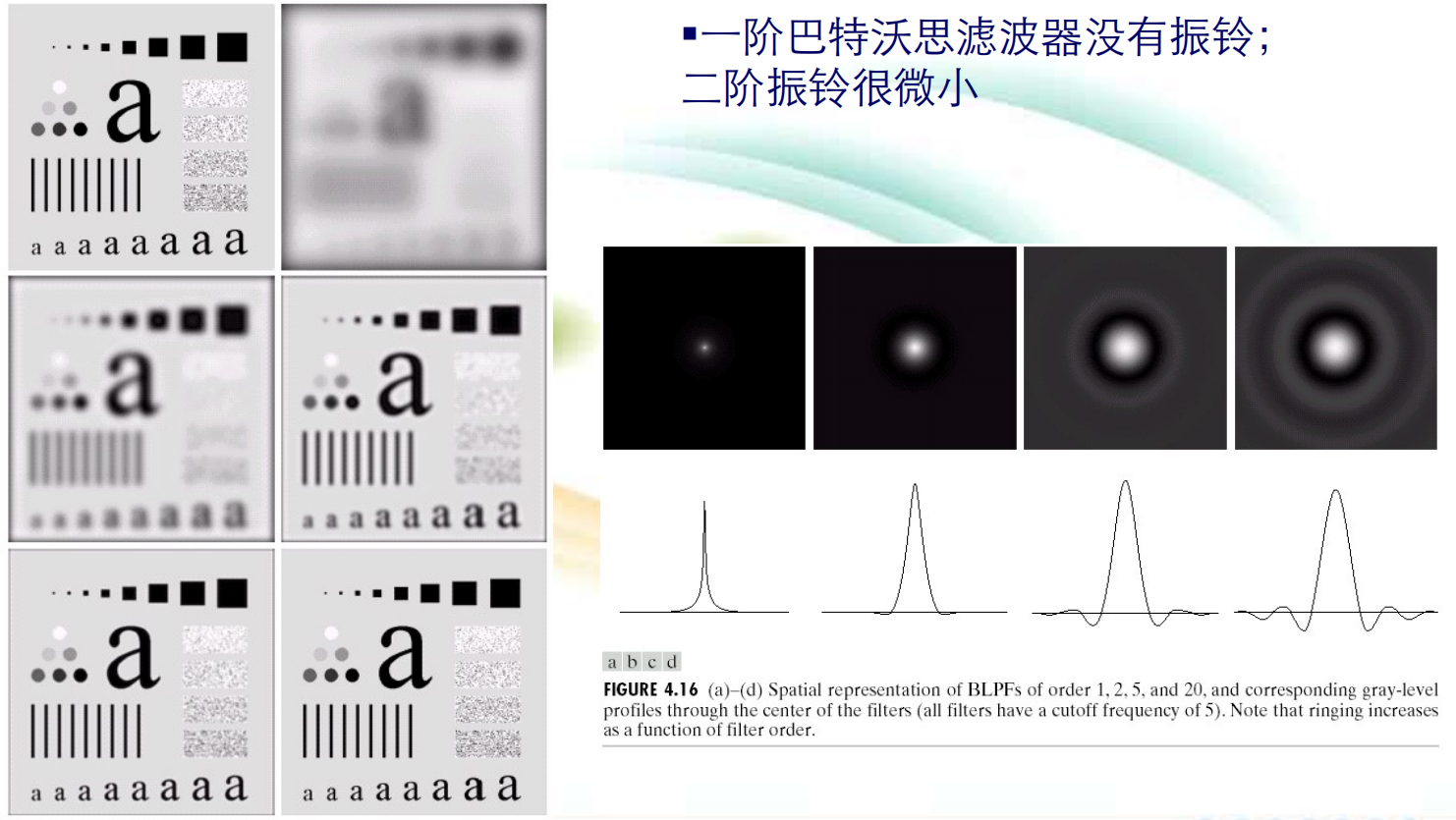 低通滤波结果图象:
低通滤波结果图象:  (2)锐化(高通)滤波: 高通滤波器可由低通滤波器得到: Hhp(u,v)=1−Hlp(u,v) 考虑三种高通滤波器:理想的、巴特沃思型和二阶高斯高通滤波器。 (3)同态滤波: 同态滤波器的基本思想 一个图像f(x,y)可以根据它的亮度和反射分量的乘积来表示 f(x,y)=i(x,y)r(x,y) 其中:i(x,y)为亮度函数,r(x,y)反射分量函数。通过同时实现压缩亮度范围和增强对比度,来改进图像的表现。 同态滤波的目的:消除不均匀照度的影响而又不损失图象细节。 同态滤波器依据 :
(2)锐化(高通)滤波: 高通滤波器可由低通滤波器得到: Hhp(u,v)=1−Hlp(u,v) 考虑三种高通滤波器:理想的、巴特沃思型和二阶高斯高通滤波器。 (3)同态滤波: 同态滤波器的基本思想 一个图像f(x,y)可以根据它的亮度和反射分量的乘积来表示 f(x,y)=i(x,y)r(x,y) 其中:i(x,y)为亮度函数,r(x,y)反射分量函数。通过同时实现压缩亮度范围和增强对比度,来改进图像的表现。 同态滤波的目的:消除不均匀照度的影响而又不损失图象细节。 同态滤波器依据 :
- 图像的亮度分量的特点是平缓的空域变化,而反射分量则近于陡峭的空域变化 。
- 这些特性使得将图像的对数的傅立叶变换的低频部分对应于。亮度分量,而高频部分对应于反射分量 – 尽管这种对应关系只是一个粗略的近似,但它们可以用于优化图像的增强操作。
- 一个好的控制可以通过用同态滤波器对亮度和反射分量分别操作来得到。
- 这个控制要求指定一个滤波器函数H(u,v),它对于傅立叶变换的低频和高频部分的影响是不同的。
同态滤波流程: 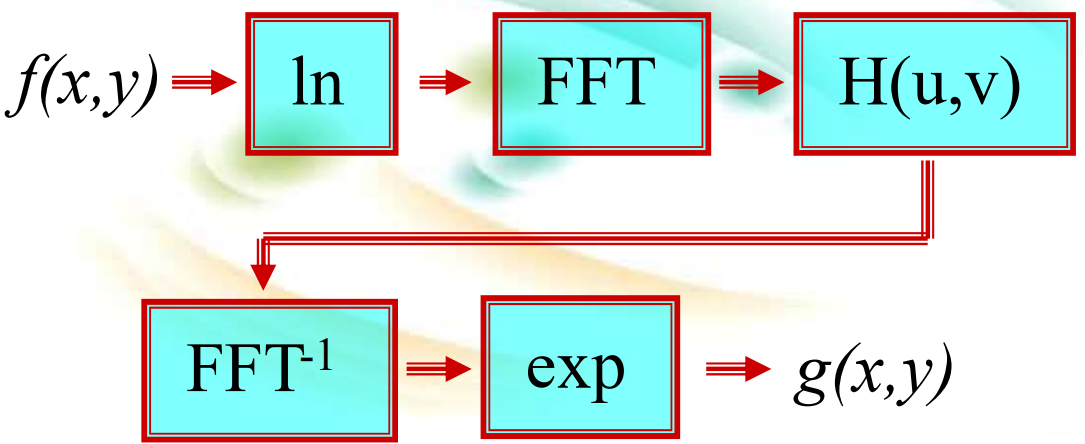


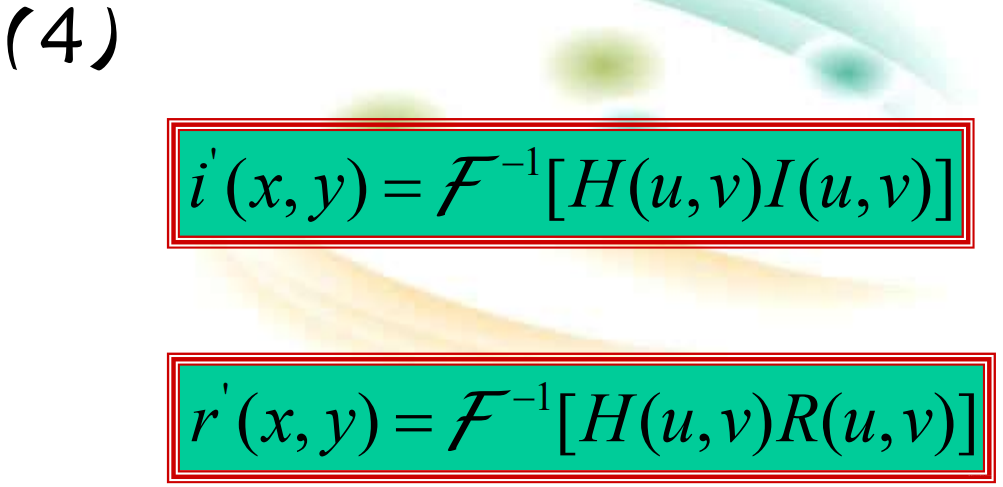

- 主要应用
印刷中的细微层次强调。弥补扫描、挂网对图像的钝化;超声探测成象,分辨率低,边缘模糊,通过锐化来改善;图像识别中,分割前的边缘提取;锐化处理恢复过度钝化、暴光不足的图像;图像创艺(只剩下边界的特殊图像);尖端武器的目标识别、定位。
我的微信公众号名称:深度学习与先进智能决策 微信公众号ID:MultiAgent1024 公众号介绍:主要研究分享深度学习、机器博弈、强化学习等相关内容!期待您的关注,欢迎一起学习交流进步!




