准备了半年多的博士考试终于结束了!现在开始整理半年来没来得及发的一些技术总结。
“C/C++ 图像处理”系列文章是随着本人做东西的先后写成的,文章的前后关系可能不太明显,在这里先跟关注专栏的各位老哥说声抱歉,在“深度学习”系列文章中会尽量改掉这个较为随意的风格,让文章更具可读性。
之前做的项目有关于“图像细化”方面的应用,因此研究了ZhangSuen细化算法,在这里总结一下:
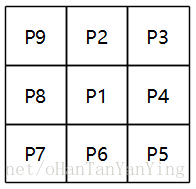
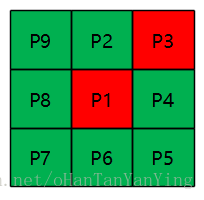
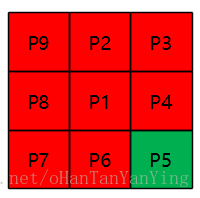
首先见上图,其表示3*3的像素块,且每个像素都贴了标签,以更好的解释算法。另外,本人用红色表示前景像素,用绿色表示背景像素,如下图所示,P9为前景像素,P4为背景像素,而P1为目标像素,也就是我们正要判断它该不该被细化掉的像素点。
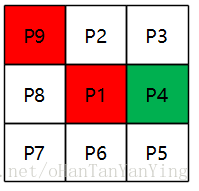
下面正式描述一下该算法,算法分两步:
第一步:循环所有的前景像素点,对符合如下条件的像素点标记为删除:
1. 2 ≤ N(p1) ≤ 6——N(p1)表示跟P1相邻的8个像素点中,为前景像素点的个数
2. S(P1) = 1——S(P1)表示将p2-p9-p2之间按序前后分别成对值为0、1的个数
3. P2 * P4 * P6 = 0
4. P4 * P6 * P8 = 0
第二步:循环所有的前景像素点,对符合如下条件的像素点标记为删除:
1. 2 ≤ N(p1) ≤ 6——N(p1)表示跟P1相邻的8个像素点中,为前景像素点的个数
2. S(P1) = 1——S(P1)表示将p2-p9-p2之间按序前后分别成对值为0、1的个数
3. P2 * P4 * P8 = 0
4. P2 * P6 * P8 = 0
可以看到一、二步的前两个条件是一样的,后两个条件有所不同。
至于为什么是这四个判断条件,我们先看第一、二步的条件1
2 ≤ N(p1) ≤ 6——N(p1)表示跟P1相邻的8个像素点中,为前景像素点的个数
如果不满足,则 N(p1)=0时,该点为孤立点,不能细化,如下图:
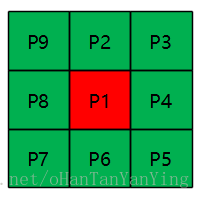
N(p1)=1时,该点为端点,不能细化,如下图:
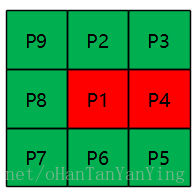
N(p1)=7时,该点为内部点,不能细化,如下图:
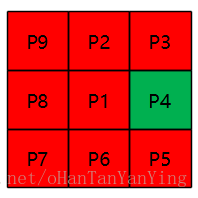
再看第一、二步的条件2
S(P1) = 1——S(P1)表示将p2-p9-p2之间按序前后分别成对值为0、1的个数
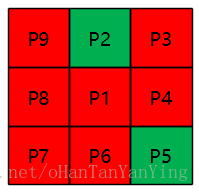
如下图所示,其中p2->p3,p6->p7就是成对值为0,1的,总共有两个。
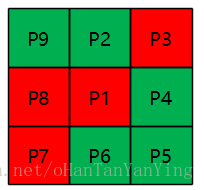
我们看不满足条件会怎么样,S(P1) = 0时,如下图所示,该种情况要么该点是内部点,要么是孤立点,都不能删除。
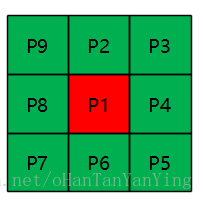
S(P1) = 2时,要么会断开,要么是内部点,显然不能删除
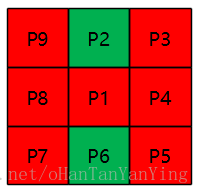
S(P1) > 2时,则断开的可能性更大,除了断开外也都是内部点,因此只有S(P1)=1满足删除的条件。
两步中不同的条件3、4最不好理解,第一步中条件3、4在P4 、P6两者之一为0时即都满足,限定删除的点是右方或者下方的点。当然,如果P4 、P6都为1,则P2、p8要都为0方满足条件,也即步骤一同样删除左上方都为空的点。
同理,可以推知步骤二删除上方或者左方的点。也删除右下方为空的点。
两者交替作用,能将对象不断的往中心细化。
上面的文字描述不是很直观,可以看看下面的图像。

对上图进行细化,步骤1和2交替进行,细化的结果如下图所示:

如果只有步骤1,则结果如下图,可以明显看到,其删除的点符合上面的推理,因为每次都删除了左上方为空的点,左上方明显倾斜。而整体细化骨架明显偏左上方,因为步骤一每次都删除右方、下方的像素。在一些情况下,细化出来的骨架甚至完全无法辨认出原来的字母是什么。就像本实验,左下方的骨架就消失了。

只做步骤二也有类似的结果,当然其比较好的是还能看出是H这个字母,但这也只是运气问题。
上面我们详细描述了ZhangSuen细化算法,下面直接上代码:
#include "stdafx.h"
#include "opencv2/highgui/highgui.hpp"
#include "opencv2/imgproc/imgproc.hpp"
#include <time.h>
#include <iostream>
using namespace cv;
using namespace std;
/*
* @brief 对输入图像进行细化,骨骼化
* @param src为输入图像,用cvThreshold函数处理过的8位灰度图像格式,元素中只有0与1,1代表有元素,0代表为空白
* @param dst为对src细化后的输出图像,格式与src格式相同,元素中只有0与1,1代表有元素,0代表为空白
*/
void thinImage(Mat & src, Mat & dst)
{
int width = src.cols;
int height = src.rows;
src.copyTo(dst);
vector<uchar *> mFlag; //用于标记需要删除的点
while (true)
{
//步骤一
for (int i = 0; i < height; ++i)
{
uchar * p = dst.ptr<uchar>(i);
for (int j = 0; j < width; ++j)
{
//获得九个点对象,注意边界问题
uchar p1 = p[j];
if (p1 != 1) continue;
uchar p2 = (i == 0) ? 0 : *(p - dst.step + j);
uchar p3 = (i == 0 || j == width - 1) ? 0 : *(p - dst.step + j + 1);
uchar p4 = (j == width - 1) ? 0 : *(p + j + 1);
uchar p5 = (i == height - 1 || j == width - 1) ? 0 : *(p + dst.step + j + 1);
uchar p6 = (i == height - 1) ? 0 : *(p + dst.step + j);
uchar p7 = (i == height - 1 || j == 0) ? 0 : *(p + dst.step + j - 1);
uchar p8 = (j == 0) ? 0 : *(p + j - 1);
uchar p9 = (i == 0 || j == 0) ? 0 : *(p - dst.step + j - 1);
if ((p2 + p3 + p4 + p5 + p6 + p7 + p8 + p9) >= 2 && (p2 + p3 + p4 + p5 + p6 + p7 + p8 + p9) <= 6)//条件1判断
{
//条件2计算
int ap = 0;
if (p2 == 0 && p3 == 1) ++ap;
if (p3 == 0 && p4 == 1) ++ap;
if (p4 == 0 && p5 == 1) ++ap;
if (p5 == 0 && p6 == 1) ++ap;
if (p6 == 0 && p7 == 1) ++ap;
if (p7 == 0 && p8 == 1) ++ap;
if (p8 == 0 && p9 == 1) ++ap;
if (p9 == 0 && p2 == 1) ++ap;
//条件2、3、4判断
if (ap == 1 && p2 * p4 * p6 == 0 && p4 * p6 * p8 == 0)
{
//标记
mFlag.push_back(p + j);
}
}
}
}
//将标记的点删除
for (vector<uchar *>::iterator i = mFlag.begin(); i != mFlag.end(); ++i)
{
**i = 0;
}
//直到没有点满足,算法结束
if (mFlag.empty())
{
break;
}
else
{
mFlag.clear();//将mFlag清空
}
//步骤二,根据情况该步骤可以和步骤一封装在一起成为一个函数
for (int i = 0; i < height; ++i)
{
uchar * p = dst.ptr<uchar>(i);
for (int j = 0; j < width; ++j)
{
//如果满足四个条件,进行标记
// p9 p2 p3
// p8 p1 p4
// p7 p6 p5
uchar p1 = p[j];
if (p1 != 1) continue;
uchar p2 = (i == 0) ? 0 : *(p - dst.step + j);
uchar p3 = (i == 0 || j == width - 1) ? 0 : *(p - dst.step + j + 1);
uchar p4 = (j == width - 1) ? 0 : *(p + j + 1);
uchar p5 = (i == height - 1 || j == width - 1) ? 0 : *(p + dst.step + j + 1);
uchar p6 = (i == height - 1) ? 0 : *(p + dst.step + j);
uchar p7 = (i == height - 1 || j == 0) ? 0 : *(p + dst.step + j - 1);
uchar p8 = (j == 0) ? 0 : *(p + j - 1);
uchar p9 = (i == 0 || j == 0) ? 0 : *(p - dst.step + j - 1);
if ((p2 + p3 + p4 + p5 + p6 + p7 + p8 + p9) >= 2 && (p2 + p3 + p4 + p5 + p6 + p7 + p8 + p9) <= 6)
{
int ap = 0;
if (p2 == 0 && p3 == 1) ++ap;
if (p3 == 0 && p4 == 1) ++ap;
if (p4 == 0 && p5 == 1) ++ap;
if (p5 == 0 && p6 == 1) ++ap;
if (p6 == 0 && p7 == 1) ++ap;
if (p7 == 0 && p8 == 1) ++ap;
if (p8 == 0 && p9 == 1) ++ap;
if (p9 == 0 && p2 == 1) ++ap;
if (ap == 1 && p2 * p4 * p8 == 0 && p2 * p6 * p8 == 0)
{
//标记
mFlag.push_back(p + j);
}
}
}
}
//将标记的点删除
for (vector<uchar *>::iterator i = mFlag.begin(); i != mFlag.end(); ++i)
{
**i = 0;
}
//直到没有点满足,算法结束
if (mFlag.empty())
{
break;
}
else
{
mFlag.clear();//将mFlag清空
}
}
}
void main()
{
Mat src = imread("4.png", IMREAD_GRAYSCALE);
GaussianBlur(src, src, Size(7, 7), 0, 0);//高斯滤波
threshold(src, src, 140, 1, cv::THRESH_BINARY_INV);//二值化,前景为1,背景为0
Mat dst;
thinImage(src, dst);//图像细化(骨骼化)
src = src * 255;
imshow("原始图像", src);
dst = dst * 255;
imshow("细化图像", dst);
waitKey(0);
}
结果如下图所示:
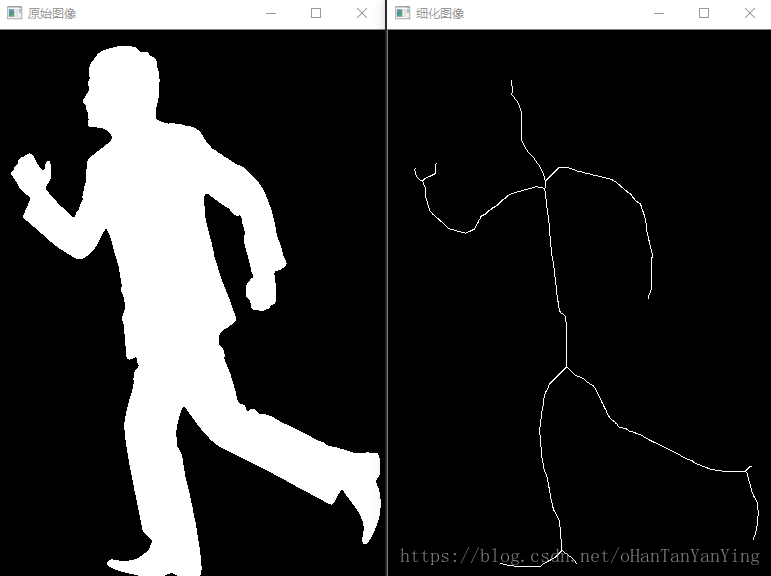
当然,如果需要获得对象的端点和交叉点,也非常简单,原理和上面的细化算法基本是一样的,这里放出实现代码和效果:
/*
* @brief 对输入图像进行端点和交叉点检测,前提是输入图像已经经过骨骼化提取
*/
void endPointAndintersectionPointDetection(Mat & src)
{
int width = src.cols;
int height = src.rows;
vector<CvPoint> endpoint;
vector<CvPoint> intersectionPoint;
//遍历骨骼化后的图像,找到端点和交叉点,分别放入容器中
for (int i = 0; i < height; ++i)
{
uchar * p = src.ptr<uchar>(i);
for (int j = 0; j < width; ++j)
{
//获得九个点对象,注意边界问题
uchar p1 = p[j];
if (p1 != 1) continue;
uchar p2 = (i == 0) ? 0 : *(p - src.step + j);
uchar p3 = (i == 0 || j == width - 1) ? 0 : *(p - src.step + j + 1);
uchar p4 = (j == width - 1) ? 0 : *(p + j + 1);
uchar p5 = (i == height - 1 || j == width - 1) ? 0 : *(p + src.step + j + 1);
uchar p6 = (i == height - 1) ? 0 : *(p + src.step + j);
uchar p7 = (i == height - 1 || j == 0) ? 0 : *(p + src.step + j - 1);
uchar p8 = (j == 0) ? 0 : *(p + j - 1);
uchar p9 = (i == 0 || j == 0) ? 0 : *(p - src.step + j - 1);
if ((p2 + p3 + p4 + p5 + p6 + p7 + p8 + p9) == 1)//端点判断
{
printf("端点:%d %d\n", i, j);
endpoint.push_back(cvPoint(j, i));
}
else //交叉点判断
{
int ap = 0;
if (p2 == 0 && p3 == 1) ++ap;
if (p3 == 0 && p4 == 1) ++ap;
if (p4 == 0 && p5 == 1) ++ap;
if (p5 == 0 && p6 == 1) ++ap;
if (p6 == 0 && p7 == 1) ++ap;
if (p7 == 0 && p8 == 1) ++ap;
if (p8 == 0 && p9 == 1) ++ap;
if (p9 == 0 && p2 == 1) ++ap;
if (ap >= 3)
{
printf("交叉点:%d %d\n", i, j);
intersectionPoint.push_back(cvPoint(j, i));
}
}
}
}
//画出端点
for (vector<CvPoint>::iterator i = endpoint.begin(); i != endpoint.end(); ++i)
{
circle(src, cvPoint(i->x, i->y), 5, Scalar(255), -1);
}
//画出交叉点
for (vector<CvPoint>::iterator i = intersectionPoint.begin(); i != intersectionPoint.end(); ++i)
{
circle(src, cvPoint(i->x, i->y), 5, Scalar(255));
}
endpoint.clear();//数据回收
intersectionPoint.clear();
}
结果如下图所示:
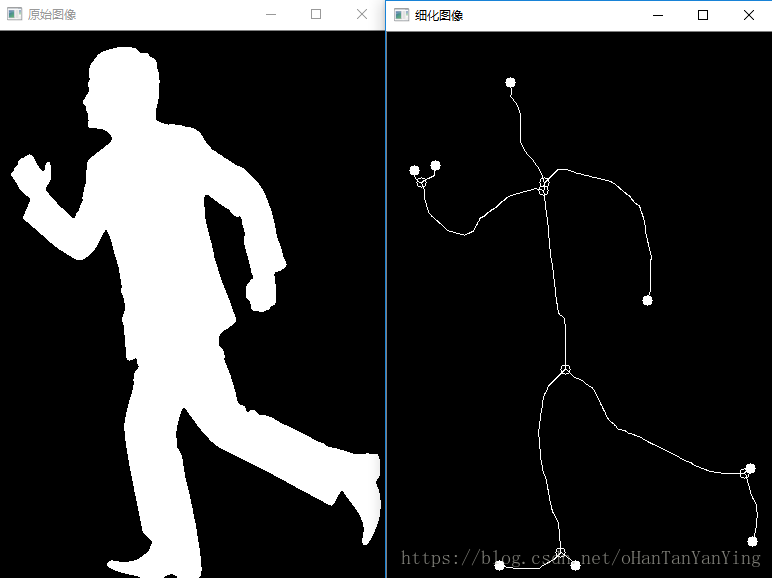
OK,到此大功告成!