经典机器学习系列(二)【线性判别分析LDA】

线性判别分析，英文名称Linear Discriminant Analysis(LDA)是一种经典的线性学习方法。本文针对二分类问题，从直观理解，对其数学建模，之后模型求解，再拓展到多分类问题。  

大体思想

给定训练样例集，设法将样例投影到一条直线上，使得同类样例的投影点尽可能接近、异类样例的投影点尽可能远离；在对新样本进行分类时，将其投影到同样的这条直线上，再根据投影点的位置来确定新样本的类别。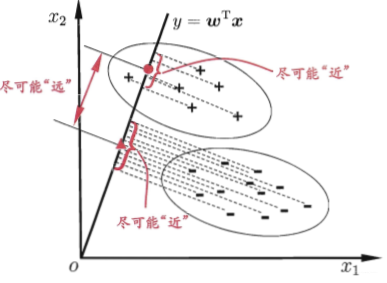  
 

数学原理

道理是这么个道理，我们现在需要在数学上对其进行分析。我们接下来先建立求解上述问题的数学模型，之后再求解。  

数学模型建立

那我们怎么从数学上去实现上述的思想呢？这里我们以二分类为例，对其展开叙述：   给定数据集
  类示例的集合、均值向量、协方差矩阵。   如果将样本投影到直线$w$上，那么样本所对应的均值和方差也将做一个线性变换，也即是投影之后的均值和方差。依据投影的数学关系，我们可以知道，原始样本的均值在$w$上的投影为wTμi​ ；原始样本的协方差在$w$上的投影为wT∑i​w；由于直线在一维空间上，所以wTμ0​、wTμ1​、wT∑0​w、wT∑1​w均为实数。   1.让同类样本的投影点尽可能接近这句话在数学上就可以表示为，让同类样本的协方差尽可能地小。即wT∑0​w +wT∑1​w尽可能地小；   2.让异类样本投影点尽可能地远离，所表示的意思就是，让两类样本的均值之间的距离尽可能地大。即
​尽可能大。   综合以上两点，组合一个最大化的目标函数J ：  
  这个式子看起来符号有点多，我们将其化简一下，定义两个量：类内散度矩阵和类间散度矩阵：  

• 类内散度矩阵(within-class scatter matrix)：

  定义类内散度矩阵Sw​=∑0​+∑1​将其展开可得：  
 

• 类间散度矩阵(between-class scatter matrix)：

  定义类间散度矩阵
  此时，最大化的目标函数J 可重写为：
  把上式称为Sb​与Sw​的广义瑞利商(generalized rayleigh quotient)。  

数学模型求解

现在的问题就变成了，我们怎么来求这个投影方向$w$，使得目标函数最大。   优化目标函数$J$的分子和分母都是关于$w$的二次项，因此求解最大化$J$与$w$的长度无关，只与其方向有关。那么我们将分母约束为1，将原问题转换为带有约束的最优化问题，再利用拉格朗日乘子法对其求解即可，原问题等价为：  
  由拉格朗日乘子法可知，上式等价于：  
  其中$\lambda$是拉格朗日乘子。  
  这里之所以可以令参数为$\lambda$，是因为整个问题我们都在求解方向，且Sb​w的方向恒为μ0​−μ1​，所以长度设置怎么好算怎么来。将  
  到这里投影方向$w$的求解就完事了。但上述解涉及到求逆矩阵，考虑数值解的稳定性，实践过程中通常将Sw​进行奇异值分解。Sw​=U∑V，这里$\sum$是一个实对角矩阵，其对角线上的元素是Sw​的奇异值，再求解，得出
 

LDA推广到多分类

将$LDA$推广到多分类问题中，假定存在$N$类，且第$i$类示例数为mi​。定义“全局散度矩阵”St​：  
  $\mu$是所有样本的均值向量。   将类内散度矩阵Sw​重定义为每个类别的散度矩阵之和：  
  用Sb​，Sw​，St​三者中的任意两者都能够构造优化目标。常见的一种构造如下所示：  
 
  $W$的闭式解为
最大广义特征值所对应的特征向量组成的矩阵，d′≤N−1。   将$W$视为一个投影矩阵，则多分类$LDA$将样本投影到d′维空间，d′通常小于原有属性数d 。于是，可通过这个投影来减少样本点的维数，且投影过程中使用了类别信息，因此$LDA$也常被视为经典的监督降维技术。   与PCA降维不同LDA降维会保留类的区分信息。在LDA二分类中，第一类的均值与第二类的均值如果重叠在一起，将会找不到投影方向。PCA与LDA并没有某一种比另外一种更好的这种说法。   本文主要参考书目，周志华机器学习。以前都没发现这书居然写地这么好。emmmm。