Matlab 仿真——直流电机速度控制（4）通过根轨迹法进行控制器设计
1. 受控对象与设计要求
受控对象
%motor parameter
J = 0.01;
b = 0.1;
K = 0.01;
R = 1;
L = 0.5;
%motor tf function
s = tf('s');
P_motor = K/((J*s+b)*(L*s+R)+K^2)设计需求（阶跃响应）：
- 稳定时间<2s
- 超调<5%
- 稳态误差<1%
2.画出根轨迹
根轨迹设计的主要思想是根据根轨迹图预测闭环响应，该图描绘了可能的闭环极点位置。然后，通过控制器添加零和/或极点，可以修改根轨迹，以实现所需的闭环响应。 本节我们使用Control system designer工具箱来协助我们进行根轨迹分析与控制器设计。 运行以下代码绘制根轨迹图
%motor parameter
J = 0.01;
b = 0.1;
K = 0.01;
R = 1;
L = 0.5;
%motor tf function
s = tf('s');
P_motor = K/((J*s+b)*(L*s+R)+K^2)
controlSystemDesigner('rlocus', P_motor) 运行结果（通过右击图像，选择Grid选项以打开网格显示）
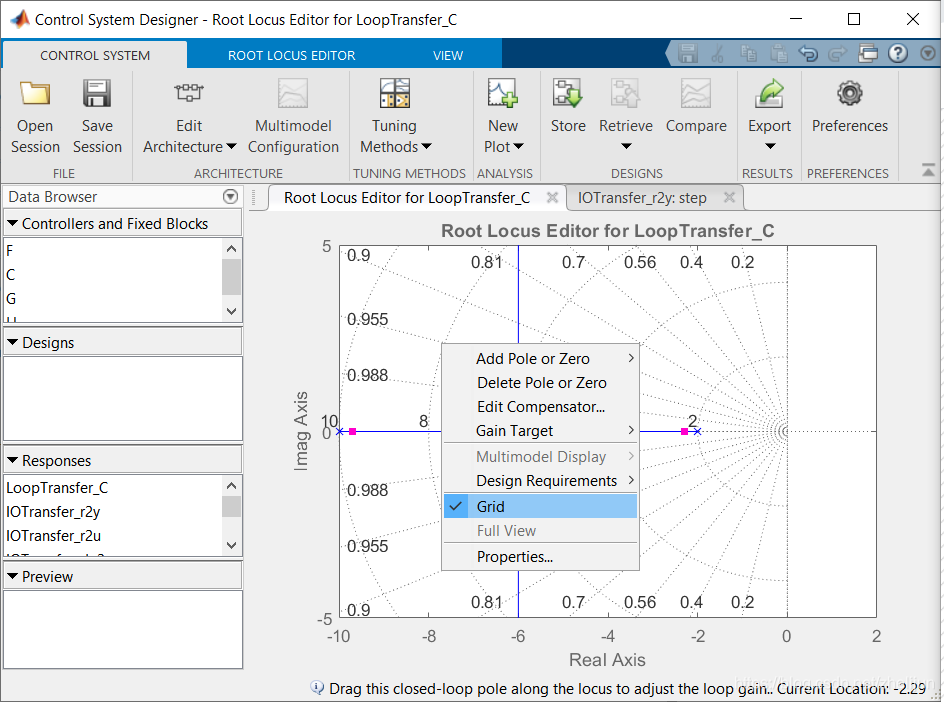
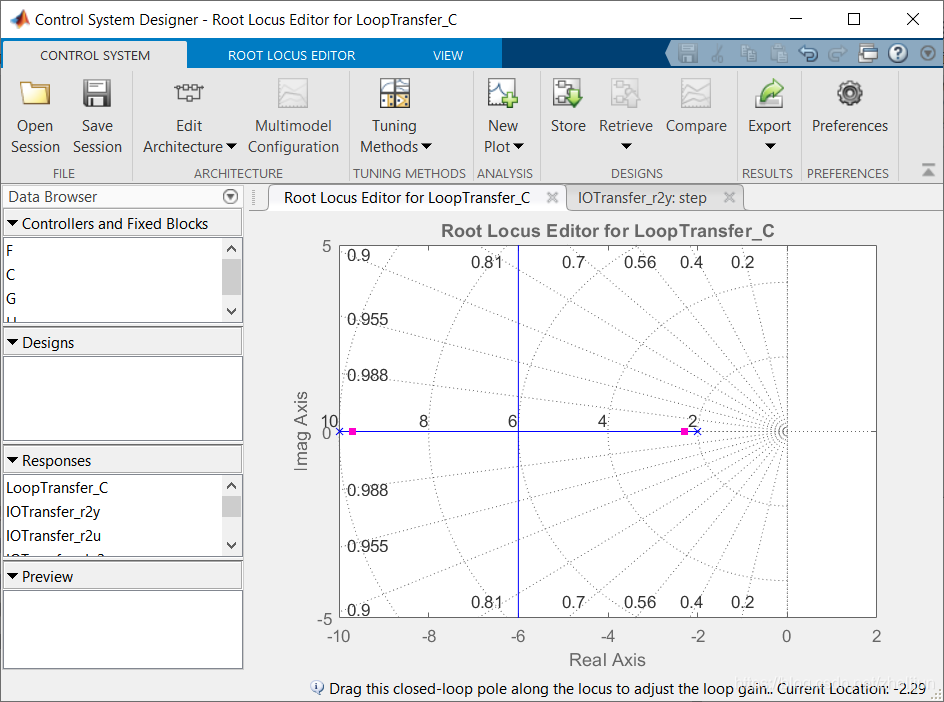
3.确定增益K
Control system designer工具箱方便我们把时域上的设计要求转换成根轨迹的区域，现在我们试着把我们的设计要求添加进根轨迹图里面 1.右击图像，选择添加设计需求
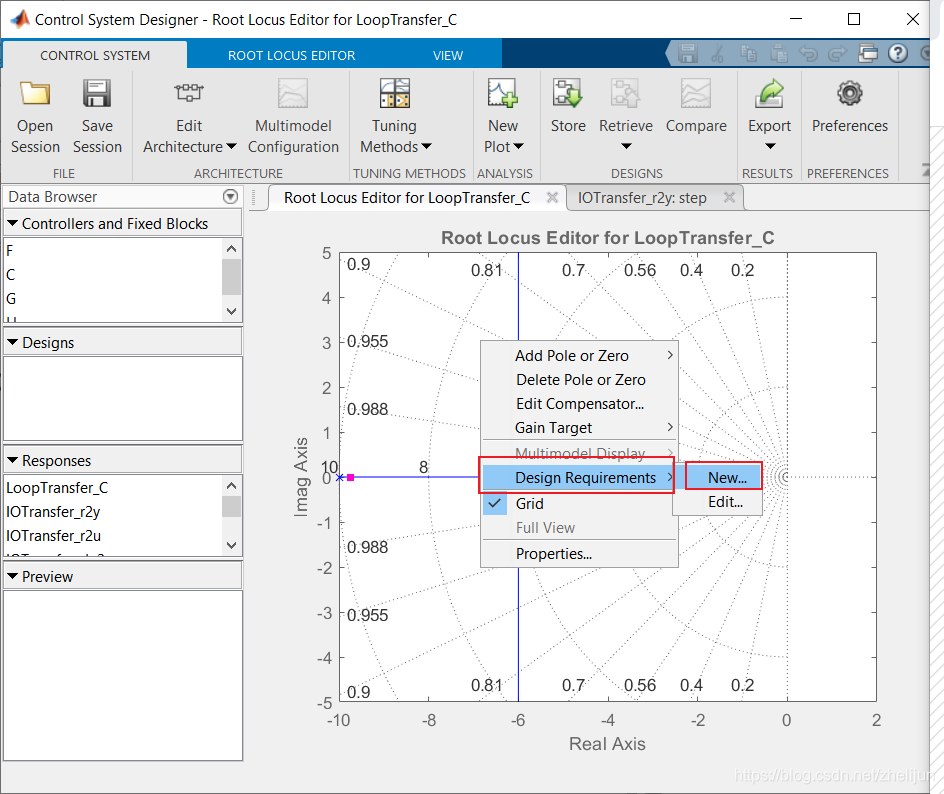2.设置Setting time小于两秒，然后点击OK
3.接着再加上超调的设计要求
上图白色区域就是满足超调和稳定时间条件的所有极点位置。通过鼠标点击粉色方块并拖动它，我们可以找到新的根位置。松手之后响应的阶跃响应图像也会随之更新。我们把极点拖到大概6±2i的位置，然后切换到阶跃响应图像，观察新系统的性能。
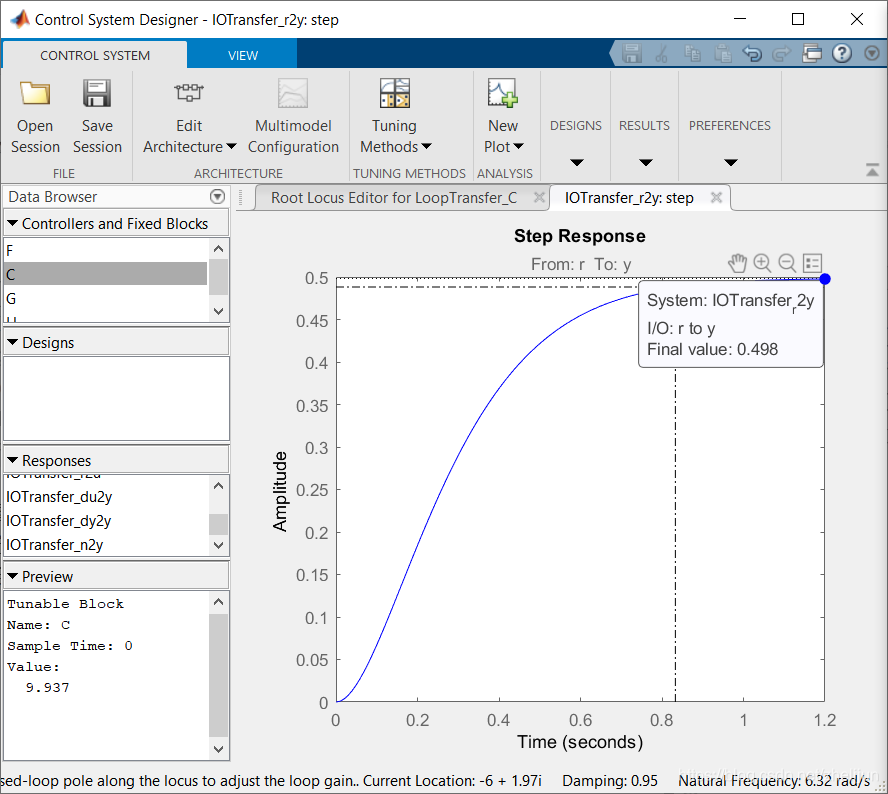新系统的超调和稳定时间都能满足要求，但是稳态误差很大。因此需要加一个lag controller来补偿稳态误差。
4.设计Lag controller
Lead compensator通常用来使系统稳定，而Lag compensator通常用来补偿系统的稳态误差。这里显然需要一个Lad compensator。我们试着添加如下的Lag 补偿器（这里为什么这么设计我们没有涉及，直接给出了结论）
利用Control System Designer工具箱可以很方便地添加Lag补偿器 4.1 点击Perference
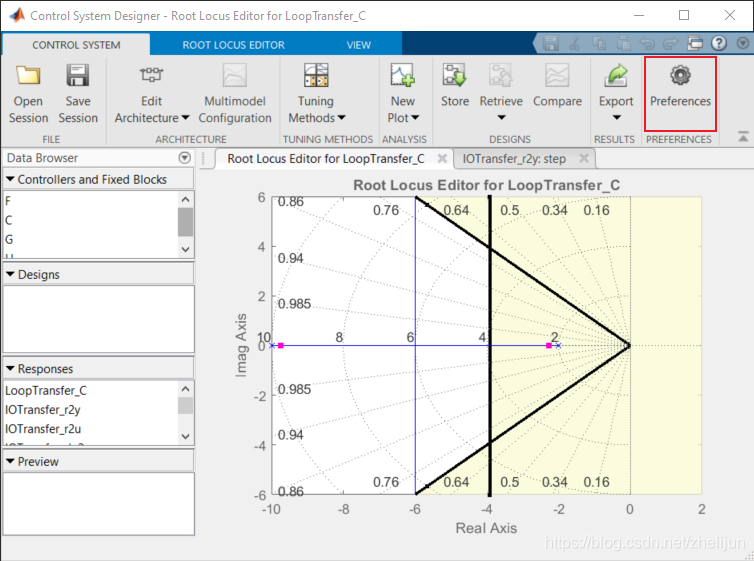4.2 点击Options， 选择Zero/pole/gain: ， 点击OK
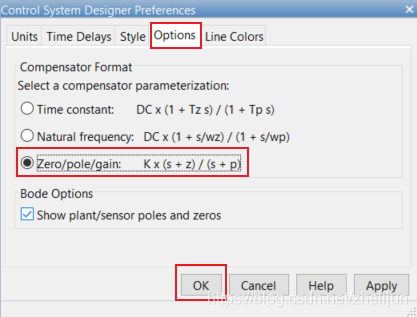4.3 双击左边Controllers and Fixed Blocks 里面的C，会打开控制器编辑窗口，我们右键单击Dynamics窗口，然后选择Add Pole and Zero，选择添加Lag 补偿器
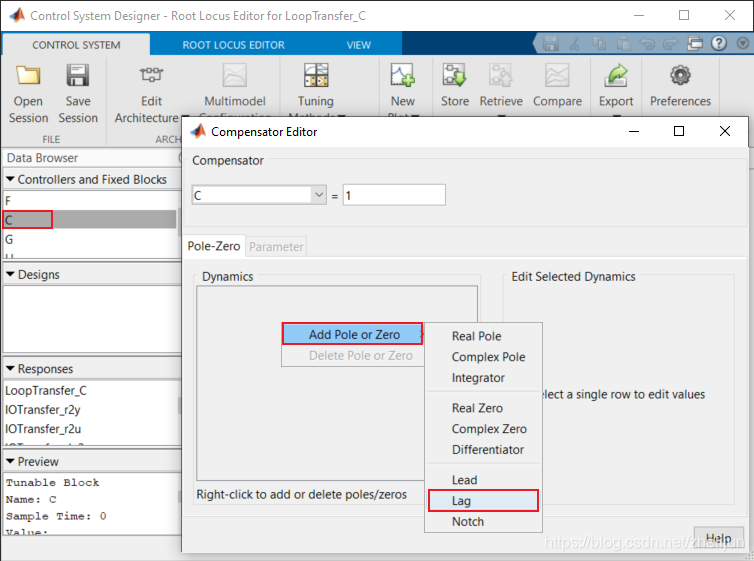4.4 配置零极点位置
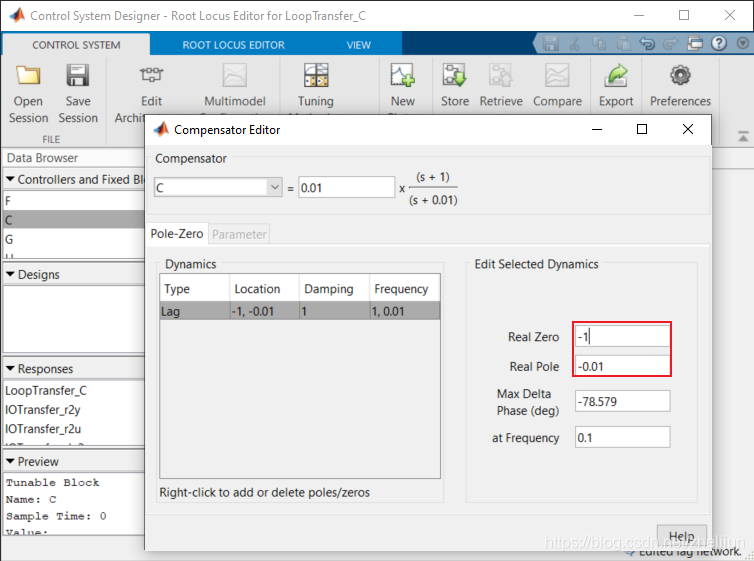关闭补偿器编辑窗口之后，根轨迹图也做了相应的更新。
5. 确定带有Lag补偿器的增益K
我们再一次拖动极点，到一个比较接近白色区域边界的位置
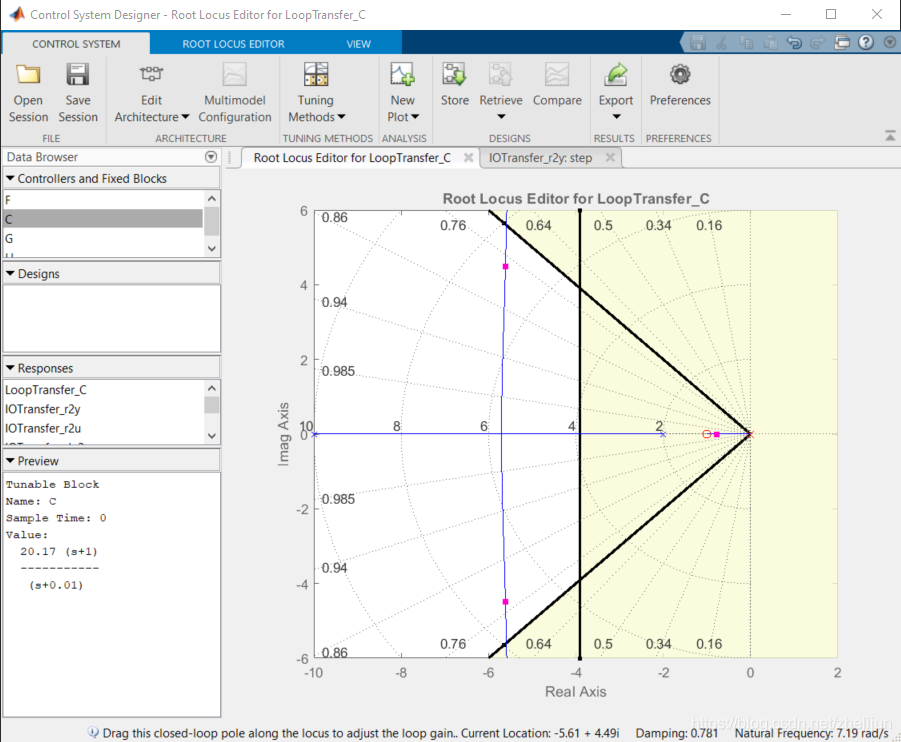
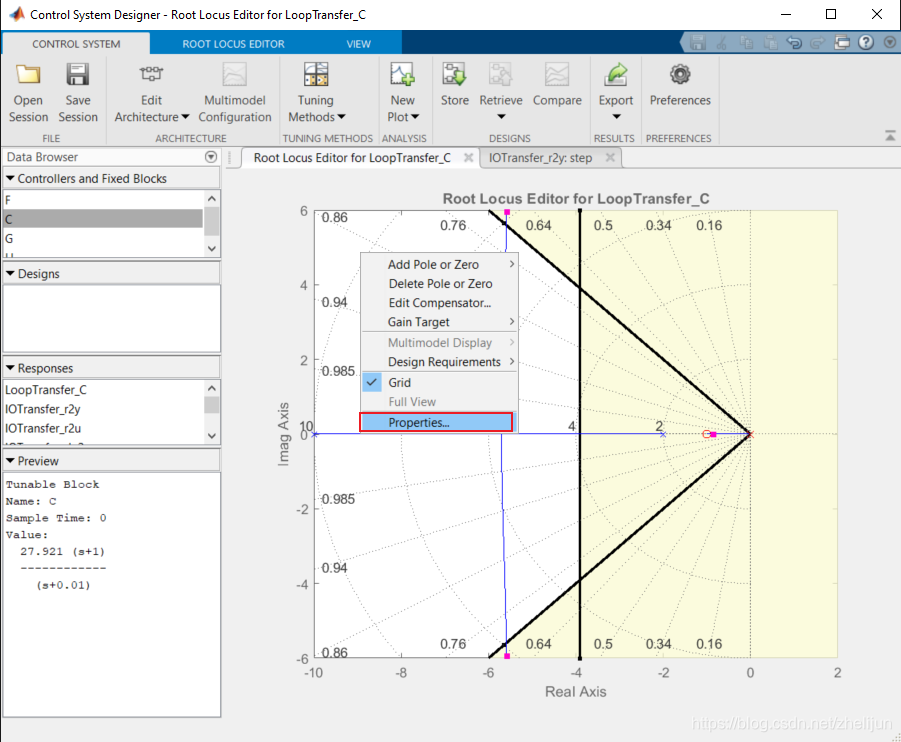
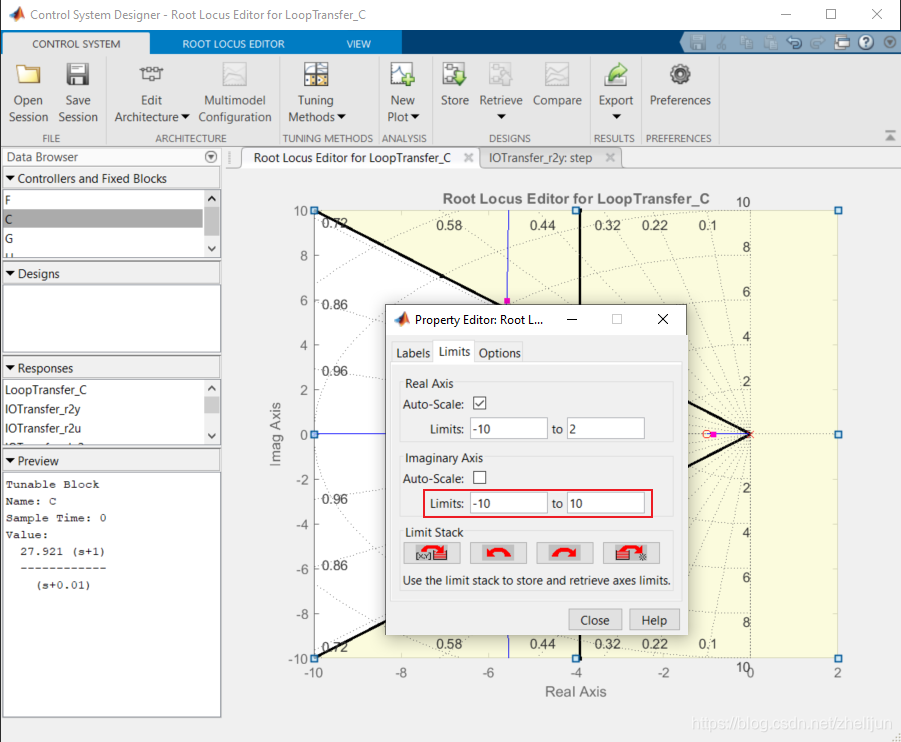
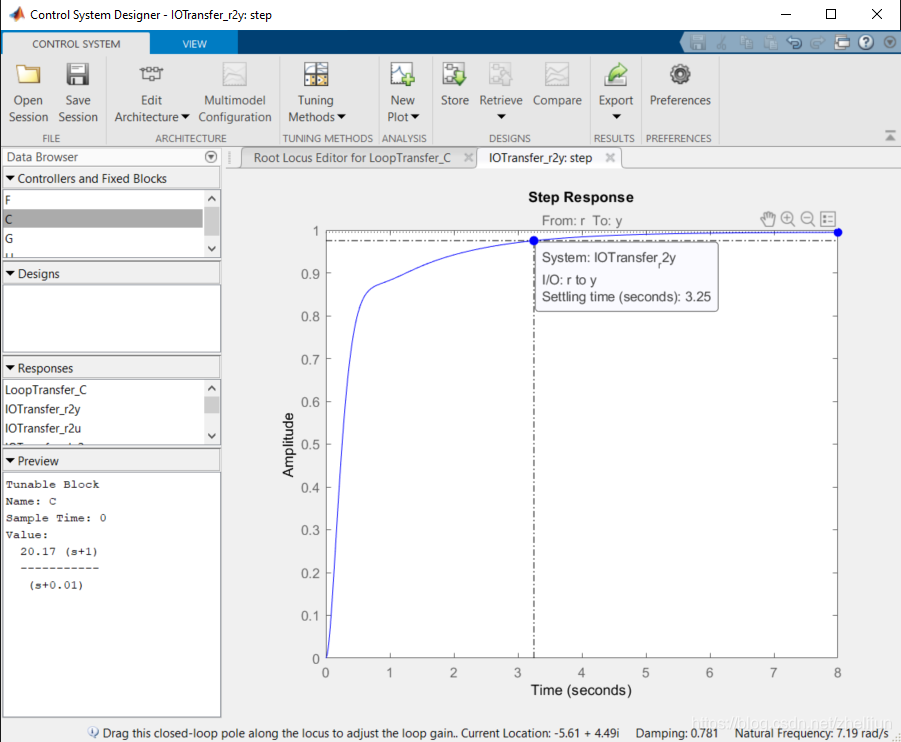然后观察阶跃响应，发现这里的稳态误差已经很小了，但是稳定时间变得不满足要求。wait,what？我们之前不是说白色区域肯定会满足超调和稳定时间要求吗？原因很简单，加了Lag补偿器的新系统已经不具备标准二阶系统的形式了，因此不能用二阶系统划分根轨迹区域的方法来划分阴影和空白区域。更具体地来说，观察根轨迹图我们发现第三个极点在很接近虚轴的位置。该极点一方面拖慢了系统的收敛（所以不满足稳定时间要求），另一方面因为它很好的衰减，所以对于新系统的超调被有所减小，因此能满足超调要求。 综上所述，对于新的系统，我们可以脱离划分的阴影区域带来的限制。我们进一步地提高增益K，看看系统怎么响应。由于图像只显示了一部分，我们调整一下虚轴的上下限 5.1 调整图像
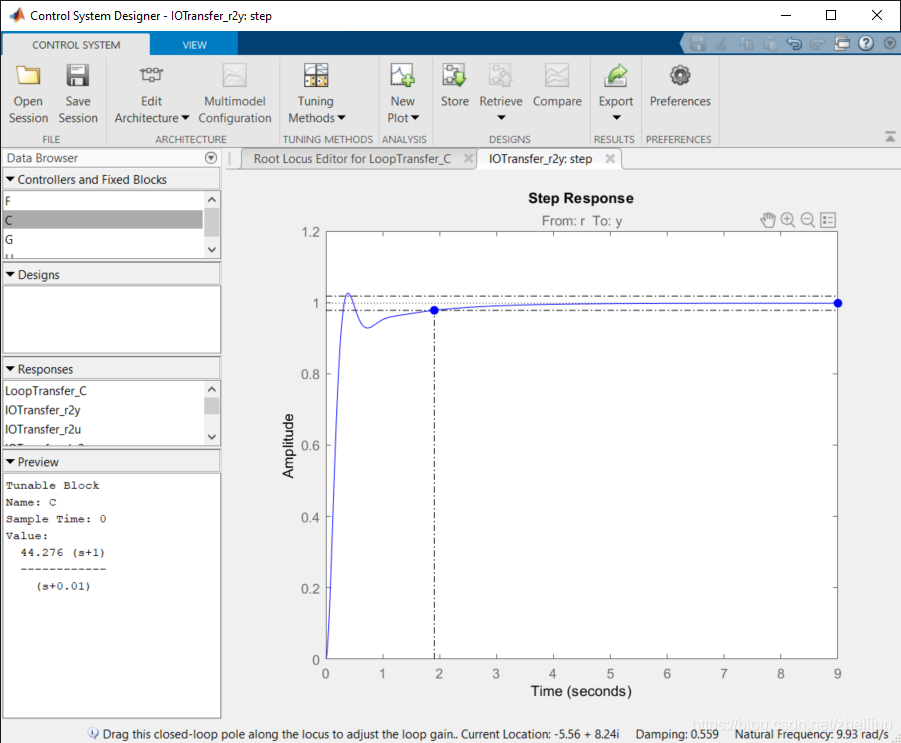
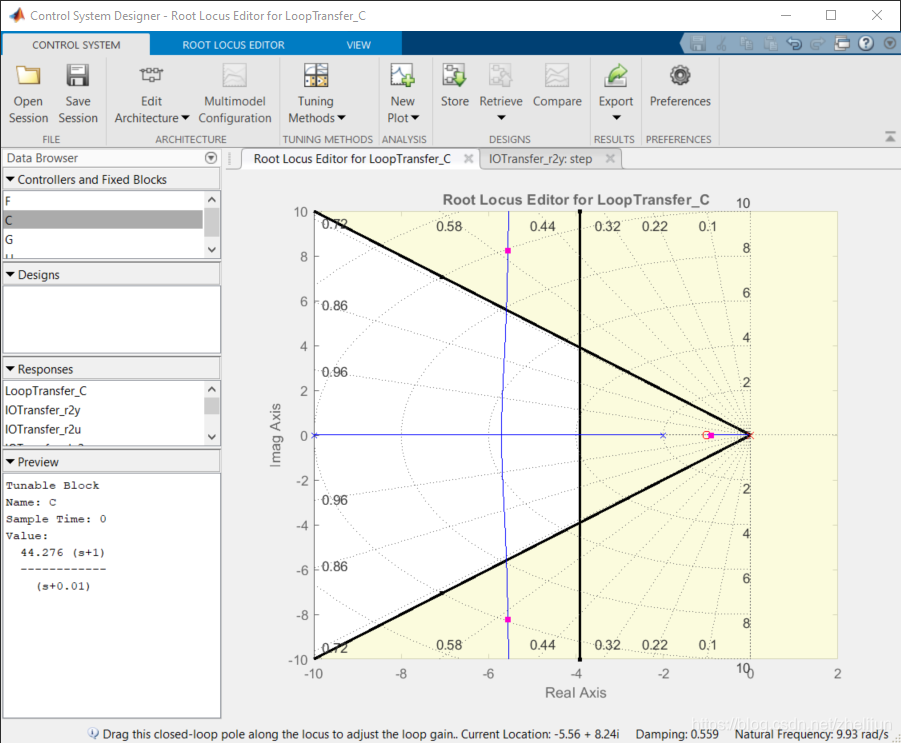
5.2 进一步拖动极点，直到阶跃响应满足系统设计要求。 我们把极点拖到了新的位置，此时的增益为44.276
新的阶跃能满足系统设计要求，至此，根轨迹法的控制器设计过程结束
