环境感知与规划专题（十）——基于采样的路径规划算法（二）_人工智能

前言

上一篇介绍了快速搜索随机树（RRT）算法的原理，这是一种基于采样的路径规划算法，在地图尺寸较大时，其效率将显著的优于基于图搜索的路径规划算法（如A*）。

然而，RRT也有其局限性，如：

狭窄通道情况下的搜索效率急剧下降
搜索得到的路径不是全局最优的

本篇将针对RRT算法应用时出现的几个问题展开讨论，并阐述几种RRT算法的改进型。

快速获取搜索树中的相邻节点

RRT算法中有一个重要的环节——获取搜索树种距离采样点最近的节点：

该算法的效率直接影响了RRT算法的搜索效率，因此，本篇单独对其进行讨论。在工程中，我们将搜索树构建为KD-Tree（K-dimensional Tree），通过KD-Tree来搜索相邻节点，它改进的就是上图中的
$Near(x_{rand},\tau)$ 函数的效率，那么什么是KD-Tree呢？ KD-Tree(K-dimension tree)是一种对
$k$ 维空间中的实例点进行存储以便对其进行快速检索的树形数据结构。KD-Tree是一种二叉树，表示对
$k$ 维空间的一个划分，构造KD-Tree相当于不断地用垂直于坐标轴的超平面将
$k$ 维空间切分，构成一系列的
$k$ 维超矩形区域。KD-Tree的每个结点对应于一个
$k$ 维超矩形区域。利用KD-Tree可以省去对大部分数据点的搜索，从而减少搜索的计算量。对于RRT算法，我们对搜索树进行KD-Tree构建，以二维问题为例，我们取所有节点中
$x$ 方向的中位数节点为切割点，将所有节点分为两部分，再对所有节点中
$y$ 方向的中位数节点为切割点分割，以此类推，最终将搜索树中的所有节点划分完毕，即得到KD-Tree。

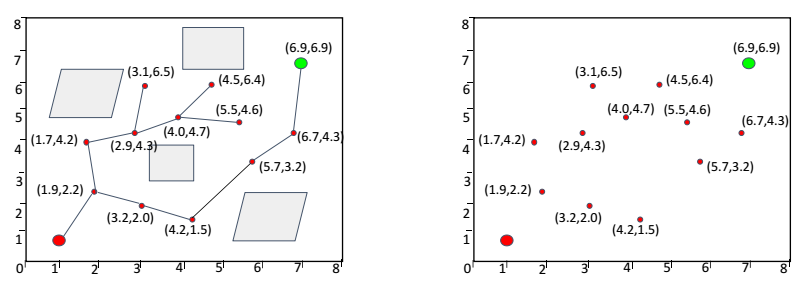
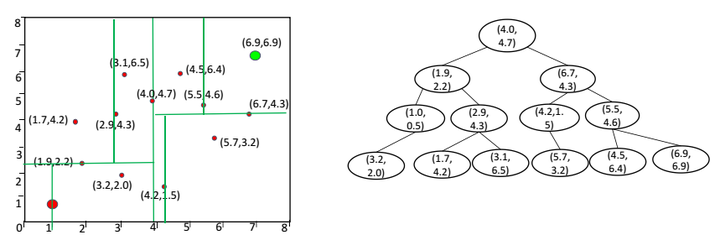
在得到KD-Tree后，我们可以根据需要，快速地搜索到距离 $x_{rand}$ 节点最近的节点，大大提高 $Near(x_{rand},\tau)$ 函数的搜索效率。

狭窄通道问题（Narrow Passage)

由于RRT算法通常采用蒙特卡洛法采样，其采样概率是均匀分布的，因此，对于狭窄通道（Narrow Passage）的情况，RRT算法的搜索效率将大大降低（搜索树的生长需要经过狭窄通道才能达到目标点，而采样点刚好落在狭窄通道的概率相对于整张地图而言较低），由此，会产生如下现象：

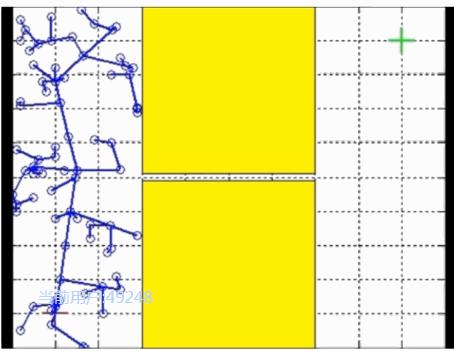
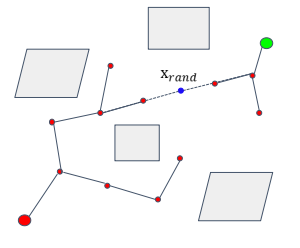
对于该类问题，我们往往采用RRT-Connect算法进行处理，如下图所示，与RRT不同的是，RRT-Connect分别从起始点和目标点构建搜索树，直到两棵搜索树相交，找到一条可通行的路径。

该算法可以大大降低Narrow Passage中由于狭窄通道采样概率较低的问题，具体的实现在此不做赘述，读者可自行搜索Bidirectional RRT / RRT Connect。

RRT * 与 Informed-RRT*

传统的RRT算法搜索得到的路径往往不是全局最优的，于是，RRT算法的改进型——RRT*应运而生。 RRT*是在 RRT算法框架基础上进行了一定的改进，算法流程如下图所示：

与RRT相似的是，我们都需要通过
$Sample$ 函数在地图中进行采样，然后在搜索树
$\tau$ 中寻找其最近的节点
$x_{near}$ 同时，在
$x_{rand}$ 与
$x_{near}$ 连线方向进行扩展得到
$x_{new}$ ，然后，我们对
$x_{new}$ 节点在地图中进行碰撞检测，若
$CollisionFree$ 则进行下一步；反之，则放弃该节点。

与RRT不同的是，RRT*中，我们在碰撞检测成功后，搜索以
$R$ 为半径，以
$x_{new}$ 节点为圆心范围内的搜索树上的相邻节点集合
$X_{near}$ ，即上图中的
$NearC(\tau,x_{new})$ 函数。

这里可以对上文提及的KD-Tree搜索方法进行一定的改进，即将
$x_{new}$ 节点与搜索树中欧氏距离小于
$R$ 的所有满足条件的叶子节点添加进相邻节点集合
$X_{near}$ 即可。

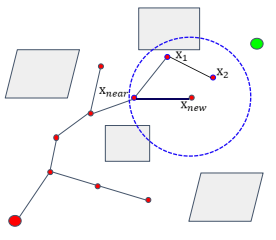
然后，在相邻节点集合
$X_{near}$ 中为
$x_{new}$ 选取其父节点，即
$ChooseParent(X_{near},x_{near},x_{new})$ 函数，该函数通过计算集合
$X_{near}$ 中所有叶子节点与
$x_{new}$ 节点的欧氏距离的最小值来选择
$x_{new}$ 节点的父节点，从而将其加入搜索树
$\tau$ 。

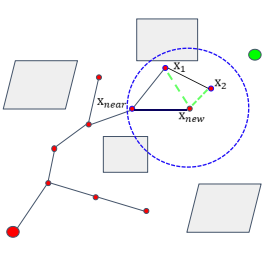
最后，我们需要对重建的搜索树进行剪枝（
$rewire$ ），该步骤也是RRT*的精髓。对于重建之后的搜索树，我们需要对
$X_{near}$ 集合中的所有叶子节点到起始节点的代价（欧氏距离）进行判断，若存在更短路径，则重新修改叶子节点的父节点，从而完成剪枝。

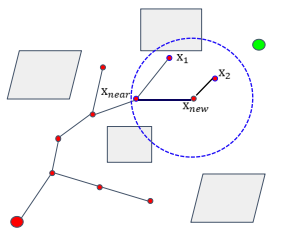
例如,
$X_{2}$ 节点的父节点原本为
$X_{1}$ ，由于
$X_{2}$ 经过
$X_{new}$ 到起始点的路径代价更小，因此，这里修改
$X_{2}$ 的父节点为
$X_{new}$ ，同理，对其他相邻节点进行类似操作，从而完成剪枝。

整个过程如下所示，可以看到，RRT* 在搜索到一条可通行路径后，并未停止迭代，而是继续剪枝。从而得到一条接近全局最优的可通行路径，因此，RRT* 较RRT在实际工程中有更广泛的应用。

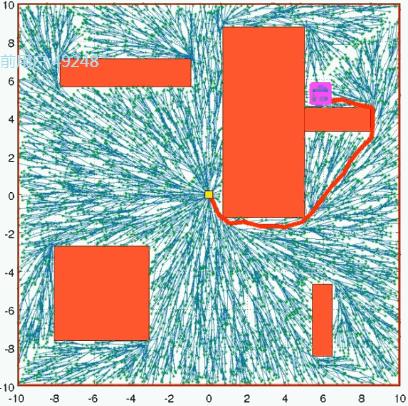
从上图可以很容易地发现一个问题，当RRT*找到一条可通行路径时，其采样函数依然在整个地图空间中进行均匀采样，然而进行剪枝等操作，那么这样的采样方式显然会耗费大量不必要的时间。

Informed-RRT* 被用于优化该问题，如下图所示，Informed-RRT* 较RRT*节省了大量的时间，究其原因在于优化了采样方式。

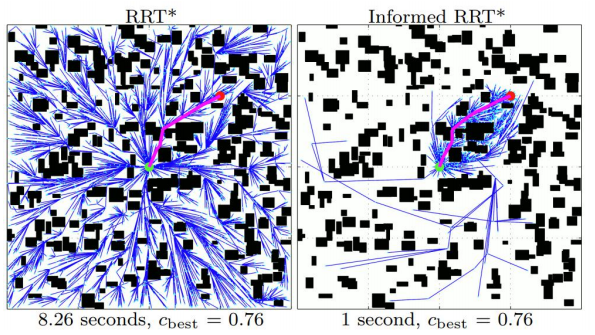
Informed-RRT* 在得到一条可通行路径的基础上，以起始点与目标点之间的连线为椭圆的长轴构建椭圆形采样区域，采样函数的采样范围被重新限制在该区域范围之中，随着搜索树的不断剪枝，椭圆范围也在不断地缩小，采样时间也随之减少，由此，大幅度节省RRT*的时间开销。

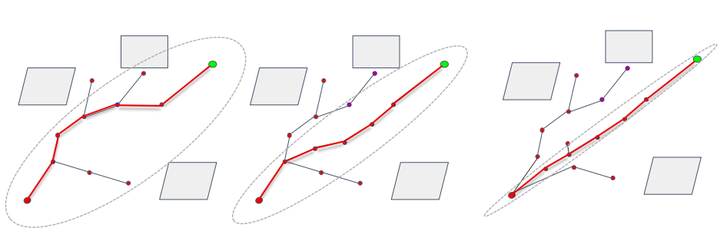
总结

本篇阐述了一种提高RRT算法搜索效率的数据结构——KD-Tree，并围绕RRT算法应用中碰到的几个问题展开，简述了RRT算法的几种改进型——RRT* 与Informed-RRT*，下一篇中将对满足动力学约束的基于采样的路径规划算法展开讨论。

作者简介： 一个被Coding耽误的无人机算法工程师，控制、导航略懂一二，热衷技术，喜欢乒乓、音乐、电影，欢迎交流。 知乎： @遥远的乌托邦 GitHub: https://github.com/DistantUtopia

前言

快速获取搜索树中的相邻节点

狭窄通道问题（Narrow Passage)

RRT * 与 Informed-RRT*

总结

您必须 登录 才能发表评论！

您必须登录才能发表评论！