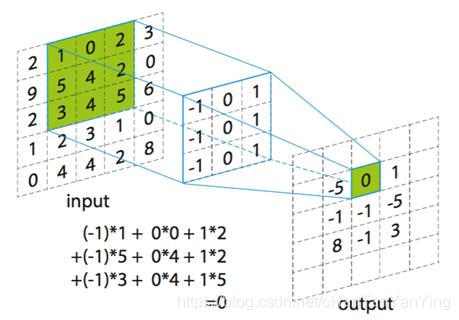
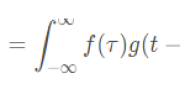得益于神经网络崛起，卷积成为近些年大热的数学词汇，不再只是待在信号处理这门要命的课程之中。 关于卷积在图像处理中的应用，操作部分看上图就明白了：假设输入图像的大小为 5 x 5，局部感受野（或称卷积核）的大小为 3 x 3，那么输出层一个神经元所对应的计算过程如上图所示。动态一点的话也可以看下面的动图。
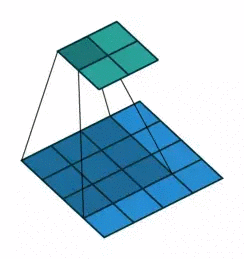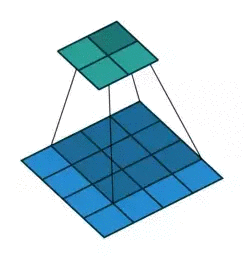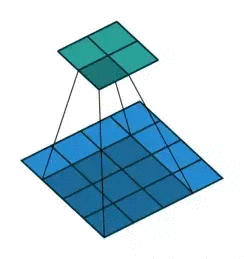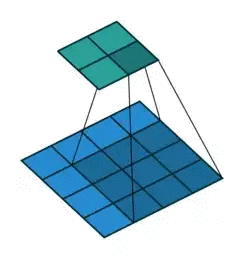而为什么要这么算，如果学过一点图像处理就很好说明，图像处理的经典边缘提取算法如canny，sobel等，或者其他一些经典算法，其实归根结底就是一个卷积过程，只不过里面的卷积核是人为设定的而已。相比于神经网络的全连接层，用卷积层更加能够快速提取到图像的局部信息，也因此更有旋转不变性等的优势，此外需要训练的参数量相比全连接也要少的多。 在实做方面，为了效率，往往会把卷积计算用矩阵来做。 假设一个卷积操作，它的输入是 4×4，卷积核大小是 3×3，步长为 1×1，输出则为 2×2，如下所示： 我们将其从左往右，从上往下以的方式展开，
- 输入矩阵可以展开成维数为 [16, 1] 的矩阵，记作 x
- 输出矩阵可以展开成维数为 [4, 1] 的矩阵，记作 y
- 卷积核可以表示为 [4, 16] 的矩阵，记作 C，其中非 0 的值表示卷积对应的第 i 行 j 列的权重。
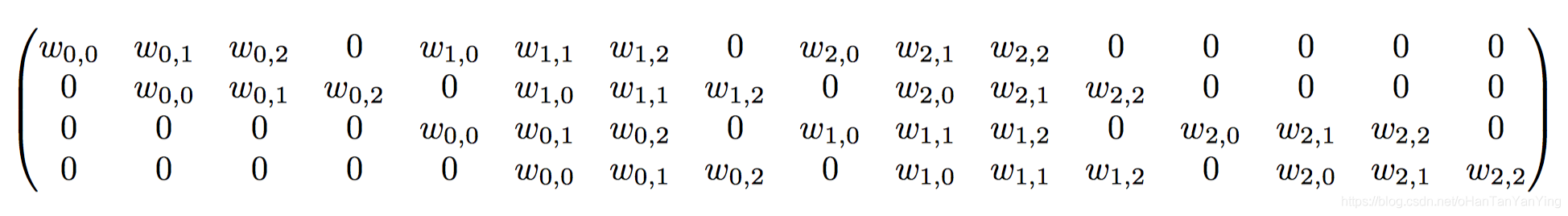
- 所以卷积可以用 y = C ∗ x = [ 4 , 16 ] ∗ [ 16 , 1 ] = [ 4 , 1 ] y = C * x = [4, 16] * [16, 1]=[4, 1]y=C∗x=[4,16]∗[16,1]=[4,1]来表示
那卷积就说完了（padding那些并没提及，后面再补吧，比较简单）。 下面看看转置卷积。它火起来应该是从FCN（Fully Convolutional Networks for Semantic Segmentation）这篇论文开始的。该论文提出了一种全卷积神经网络，然后通过转置卷积对最后一层（或者倒数几层）进行上采样，将图像的大小恢复到与输入图像一样，该文章为语义分割指出了一条明路，也使得转置卷积看起来非常高大上。但其实，这个东西并没有什么神奇的。。。 首先再看一下
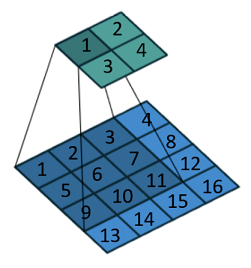卷积的示意图，下面的1只参与生成上面的1，而下面的2参与生成上面的1、2。那么我们能不能反过来，把这一过程逆向呢？答案是可以的，就是下面这张图：
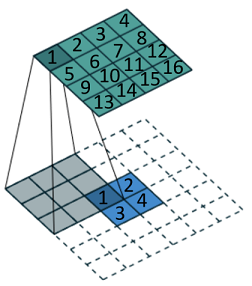我们把小图像按照需要扩展一下（下面虚线部分），然后其他部分按照卷积那么算就可以了。它得到的大小会跟卷积前的一样。巧妙的是上面的1只受下面的1影响，而上面的2受到下面的1、2影响，刚刚好就是一对逆向关系。如果把现在的小图像写在右边，卷积核矩阵写在左边，那么该卷积核矩阵写出来刚刚好就是正常卷积的卷积核矩阵的转置。所以这种卷积叫做转置卷积。 这里面有个问题可以稍微看下，那就是对原图做卷积然后再做转置卷积的过程是一个从大到小再到大的过程，那么开始和结束是一样的吗？ 答案是不一样的，这个过程会丢失图像信息。至于丢多少主要取决于中间的”小”能保存多少。但这对于语义分割是OK的，因为我们最终要得到的信息会比原图少的多。 另外在本人看来，因为神经网络的权重都是要训练之后得出来的，因此其实转置卷积和正常卷积看起来真的没有多大的不同，不过就是在正常卷积不填充的情况下会把图像变小，而转置卷积一定会填充而把图像变大罢了。 在pytorch中使用转置卷积的代码如下：
# coding:utf-8
from PIL import Image
import numpy as np
import torchvision.transforms as transforms
import torch
from torch import nn
x=Image.open("demo.jpg")
x.show()
x=transforms.ToTensor()(x)
x=torch.unsqueeze(x,0)#添加一个维度
conv_trans = nn.ConvTranspose2d(3, 3,(12,12), 2)# 定义转置卷积
y=conv_trans(x)#转置卷积计算
y=torch.squeeze(y)#扔掉一个维度
#结果显示
imgout=transforms.ToPILImage()(y)
print(x.shape)
print(y.shape)
imgout.show()
原图
结果：
从图上可以看到，pytorch在初始化的时候应该已经将转置卷积核参数设置成特征提取的形式了。 参考文章： https://www.jianshu.com/p/09ea4df7a788?utm_source=oschina-app https://cloud.tencent.com/developer/article/1363619
