二维点云ICP原理推导
描述
ICP是迭代就近点算法,大部分的实现代码都是基于PCL点云库的,也就是三维点云的匹配
实际上,二维点云数据也算是常见的数据类型,比如移动机器人经常使用的单线雷达。本文就是二维点云ICP的原理推导
算法原理
二维点云数据说明

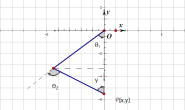
现在假设我们有两帧点云A与B,我们把 A 称为标准点云,把 B 称为源点云。我们的需求是把点云 B 经过矩阵变换到点云 A,需要注意的是点云 A 和点云 B 是在同一坐标系下。
矩阵变换计算
在同一坐标系下,将某一片点云变换到另外一片点云,需要矩阵变换的知识。
假设我们需要点云在x方向平移Δx, y方向平移Δy, 点云整体旋转θ弧度

ICP算法核心
ICP算法很简单,简单来说就是对b点云不停进行矩阵变换,把它变换到和a很接近就停止。专业的说,分为如下几步
点云归一化
找到两片点云中的对应点对
根据对应点对的信息,计算得到这次的变换矩阵
变换点云
计算当前的损失
是否决定继续迭代。如果损失小于设定阈值或者达到最大迭代数停止,否则返回执行第1步
1. 点云归一
点云归一化只是我的一个说法,实际并不完全等同传统的归一化操作。
这里做的操作是,取点云的中心(或者有权重时可以取重心,或者其他合理的点也是可以的)

接下来的一部分操作是要使用归一化后的点集 a aa 和 b bb,有一部分是要使用原来的点云 A AA 和 B BB 的,请注意区分
2. 确定对应点对
确定对应点对这是一个比较有意思的话题。什么是对应点对?
正确的理解就是,点云A和点云B的这两个点,可能原来就是一个点。但实际上,当A和B还没有经过ICP时,往往这个关系是模糊的,没有人能够说出哪两个点是对应的。那该怎么办呢?好啦,ICP的核心来啦。
ICP算法的对应点对,计算欧式距离最近的被认为是对应点对,也就是ICP的C,closet
具体实施上可以这样做,经过归一化后的点集 a 和 b 中,a i 的对应点 b j 是
在PCL库的ICP算法过程中,有一个很重要的步骤就是对应关系去除。原因是数据是有噪声的,因此要去除对配准有影响的错误点对。
二维点云的数据量是小的,那么请你结合自己的需求来完成去噪这一步。这一步是必要的。
3. 变换矩阵计算
先明确到了这一步我们拥有的数据和要得到的东西。我们有的是很多对应的点对,我们要求的是一个变换矩阵,使用这个矩阵完成变换后,这些对应的点对的距离和是最小的(意思就是说,这个矩阵至少是当前最优的,使用这个矩阵相比于其他任何变换矩阵,能让牛郎们和织女们的距离和最小)。那么我们就来进行公式推导吧。(数学老师说的没错,数学真的很重要)

误差函数值E ( R , t ) 越大,总的距离和越小。
在这里我好好推一下公式,说明一下这是怎么得到的吧
距离和函数为D ( R , t ) D(R,t)D(R,t)其实就是对所有的对应点对距离来求和。直接写成矩阵形式会更好理解

这步推导我真的不写详细在这里,因为已经真的很简单了,推到下一步如下

旋转弧度θ θθ的计算如下
旋转矩阵 R RR 因此也能得到
平移向量t tt的计算方式如下

解释一下也很简单,本来是可以A中心减B中心的,但是刚才已经证明了经过旋转矩阵 R RR 会令点对距离和更小,因此B的中心点位置也就同时经历矩阵 R RR 的变换
4. 变换点云
第三步我们已经求出了旋转矩阵 R RR 和平移向量 t tt,接下来就是将原点云进行矩阵变换了。注意,是原来的点云 A 和点云 B ,而不是归一化后的点云 a 和点云 b。为什么?你的操作对象一直是点云 A 和点云 B ,归一化后的 a 和 b 只是你需要的中间变量而已对源点云 B 做变换,得到新的点云 B ′
′
5. 计算损失
将最新变换出的矩阵 B ′ ,与你的目标点云 A 进行计算。可以自行设计属于自己的损失函数,来表示两片点云究竟匹配的怎么样。
我在这里设计的损失函数仍然是对应点对(最近点)的距离之和
6. 是否继续迭代
接下来就要看这个计算出的 L o s s 值能否满足你的要求了。
迭代终止条件的设计其实比较自由。但我的经验告诉我,比较常见的是以下几种
L o s s < L o s s m i n : 当前迭代得到的损失值小于了设定的最小阈值了
i t e r a t i o n < i t e r a t i o n m a x : 迭代次数超过了最大迭代次数
Δ L o s s <Δ L o s s m i n : 损失值的变化小于了设定的最小变化值
分别代表的意义也是明显的:1)当前已经匹配的很好了,别迭代了;2) 已经匹配了好多次了,饭都凉了;3)这一次都没提升多少,你还继续匹配干嘛
结束语
这篇文章我真的写了好久了,公式都是我生推的,分析都是生写的,给个赞吧哈哈,谢谢