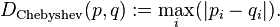在数据挖掘的过程中，只用用到了相似性（如物品之间的相似性、人之间的聚类等），就会涉及到距离的运用。怎样选择合适的距离，对最终数据挖掘的准确性非常关键。因此，这里总结了比较常用几种距离算法和常用的计算场景，供大家参考：
1. 欧拉距离
2. Pearson距离
Pearson是推荐时最常用的一种距离，对于评分、喜好等用户评判标准不一样的时候特别有用。可以化为两向量规范化后的乘积，其本质是两个向量是否同升同降。
Pearson相关系数：
3. 杰卡德距离
杰卡德距离在求两个集合的相交程度时比较有用，一般应用于布尔类型的向量中。应用场景，如两首音乐的被共同喜欢的程度、两个人性格的相似程度等
4. 夹角余弦距离
余弦距离不关心向量的长度，而只关心向量的夹角余弦。应用场景，如文本分类时，两文本之间距离计算。
夹角余弦距离比pearson距离更加严格。因为对于pearson来说，就算两个向量之间有夹角，只要其同升同降，其person的相关系数是1，即距离为0。
而对于夹角余统来说，其距离是他们之间的夹角。
更通俗点来说，pearson距离跟向量之间是否同升同降有关系，而余弦距离除了跟向量之间是否同升同降有关系外，还跟余弦他们升降的程度有关。
5. 曼哈顿距离
曼哈顿距离，顾名思义，城市街区距离。主要应用场景，如棋盘、城市里两个点之间的距离等
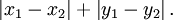
6. 汉明距离
两个字符串之间的距离，用于计算之间的相似度。应用场景如钓鱼网站与正规网站之间相似程度、两作文是否作弊等。
计算方法，把S1变成S2所需要进行替换的最小次数。
7. 马氏距离
马氏距离表示数据的协方差距离。马氏距离与欧氏距离的不同之处在于，马氏距离考虑了各个维度之间的联系(如身高与体重)，并且独立于测量尺度（米、千克等不同量纲）。
设多变量向量为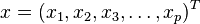
，多变量均值为
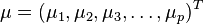，协方差距阵为
，则马氏距离为：
可以出，当协方差距阵为单位距离时，马氏距离退化为欧氏距离。
8. 切比雪夫距离
国际象棋棋盘上二个位置间的切比雪夫距离是指王要从一个位子移至另一个位子需要走的步数。由于王可以往斜前或斜后方向移动一格，因此可以较有效率的到达目的的格子。
若二个向量或二个点p 、and q，其座标分别为p_i及q_i，则两者之间的切比雪夫距离定义如下：
开心洋葱 , 版权所有丨如未注明 , 均为原创丨未经授权请勿修改 , 转载请注明位置距离常用算法总结！
