Turtlebot+ROS Stage仿真环境实现MPC轨迹跟踪

在无人车系统（十一）：轨迹跟踪模型预测控制(MPC)原理与python实现【40行代码】中介绍了MPC方法在无人车轨迹跟踪中的应用。以Udacity中的例子作为引子，详细介绍了MPC的原理，无人车的运动学模型，以及给出基于python的实现。Udacity的仿真器是一些特定的环境，没有ros中的stage或gazebo灵活。本文以turtlebot的轨迹跟踪任务作为引子，介绍在ROS Stage仿真环境中的实现移动机器人轨迹跟踪控制。

1. 仿真环境设置

1.1 更改stage环境地图

ubuntu 18.04+ros melodic

• 首先，请参照install turtlebot on ubuntu 18.04 + ros melodic在melodic版本的ROS中安装好turtlebot。
• 然后，参照tturtlebot_stageTutorialsindigoCustomizing the Stage Simulatorr熟悉如何在stage仿真环境中使用自己的地图，以及如何在仿真环境中增减障碍物。stage仿真环境设置过程中重要的三个文件后缀分别为：“.png,.world,.yaml”。其中”.png”为地图的图片，”.world”为整个环境的配置文件（包括地图，机器人，障碍物等），”.yaml”为地图的配置文件。因此，更改要将turtlebot stage中的原始地图更改成自己的地图，只需要将.png与.yaml文件替换原始的.png与.yaml文件。
  例如：

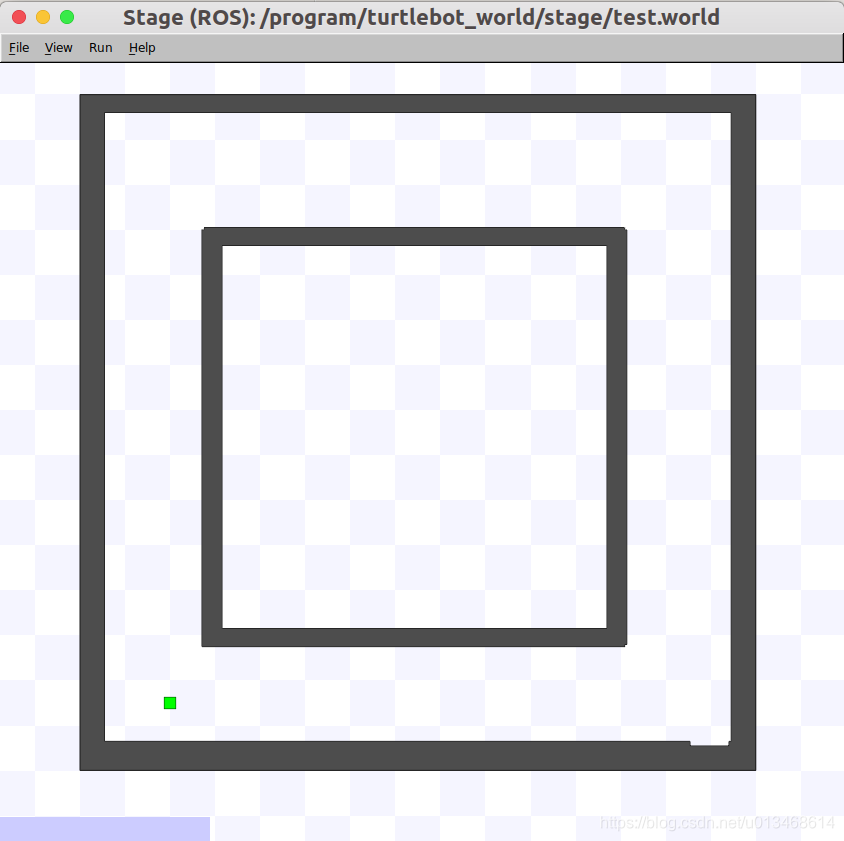
1. test.png图片为
   
2. test.yaml文件内容如下

image: test.png
resolution: 0.05
origin: [0.0, 0.0, 0.0]
negate: 0
occupied_thresh: 0.65
free_thresh: 0.196

3.stage/test.world文件内容如下：

include "turtlebot.inc"
include "myBlock.inc"


define floorplan model
(
  # sombre, sensible, artistic
  color "gray30"

  # most maps will need a bounding box
  boundary 1

  gui_nose 0
  gui_grid 0
  gui_outline 0
  gripper_return 0
  fiducial_return 0
  laser_return 1
)

resolution 0.02
interval_sim 100  # simulation timestep in milliseconds

window
(
#  size [ 600.0 700.0 ]
  size [ 600.0 600.0 ]
  center [ 0.0 0.0 ]
  rotate [ 0.0 0.0 ]
  scale 60
)

floorplan
(
  name "test"
  bitmap "../test.png"
  size [ 15.0 15.0 2.0 ]
  pose [  7.5  7.5 0.0 0.0 ]
)


# throw in a robot
turtlebot
(
  pose [ 2.0 1.5 0.0 0.0 ]
  name "turtlebot"
  color "green"
)

4.在.bashrc文件（打开.bashrc文件在终端使用命令gedit ～/.bashrc）中未尾添加如下内容，替换原始stage环境

export TURTLEBOT_STAGE_MAP_FILE=/program/turtlebot_world/test.yaml
export TURTLEBOT_STAGE_WORLD_FILE=/program/turtlebot_world/stage/test.world

5. 运行roslaunch turtlebot_stage turtlebot_in_stage.launch，发现环境地图已经成功更改为自己的地图。

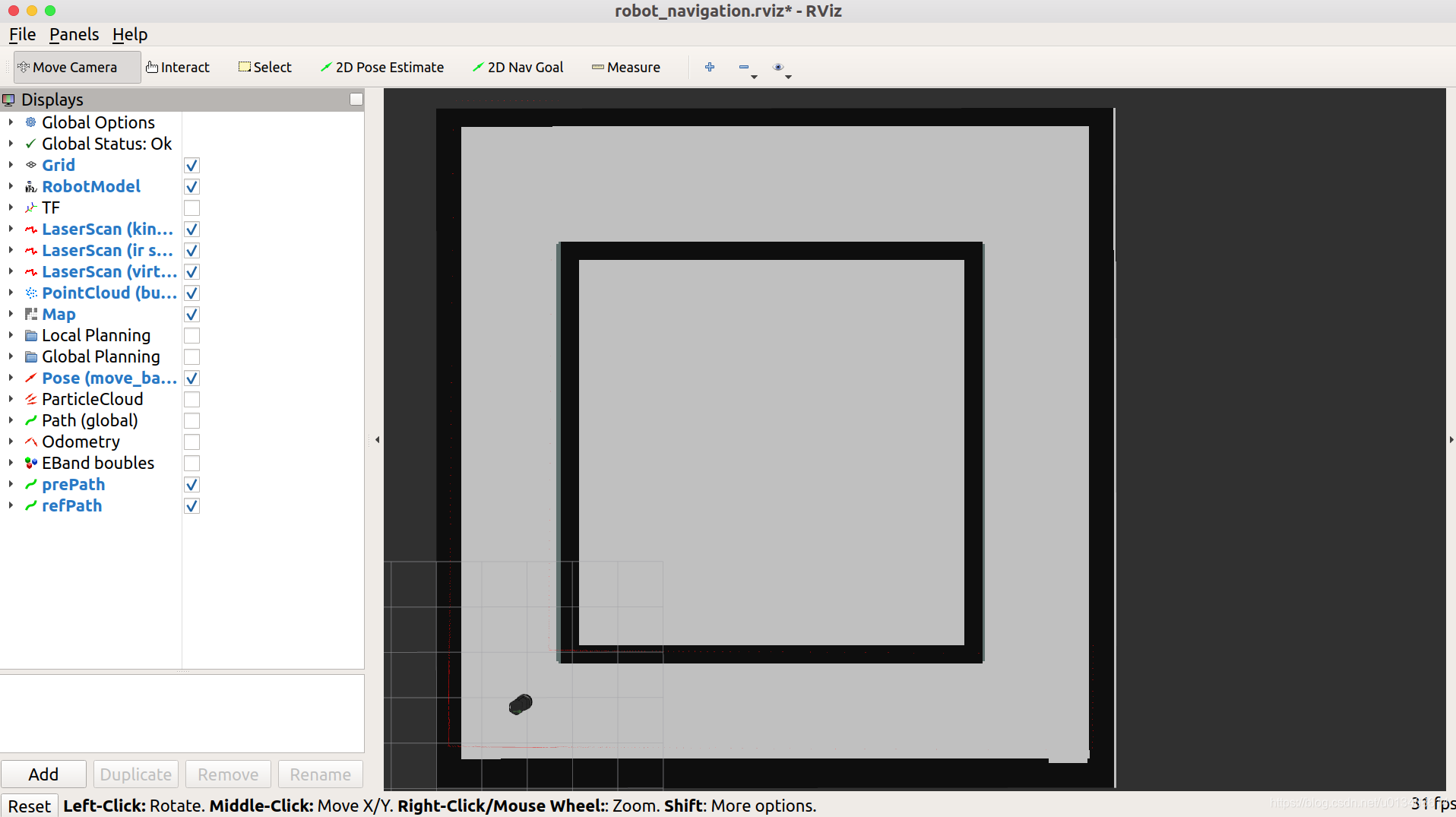
1.2 获取要跟踪的轨迹

1.2.1 获取路点

点击rviz工具栏中的”+”号，在新出现的界面中选择“PublishPoint”，点击OK退出该界面。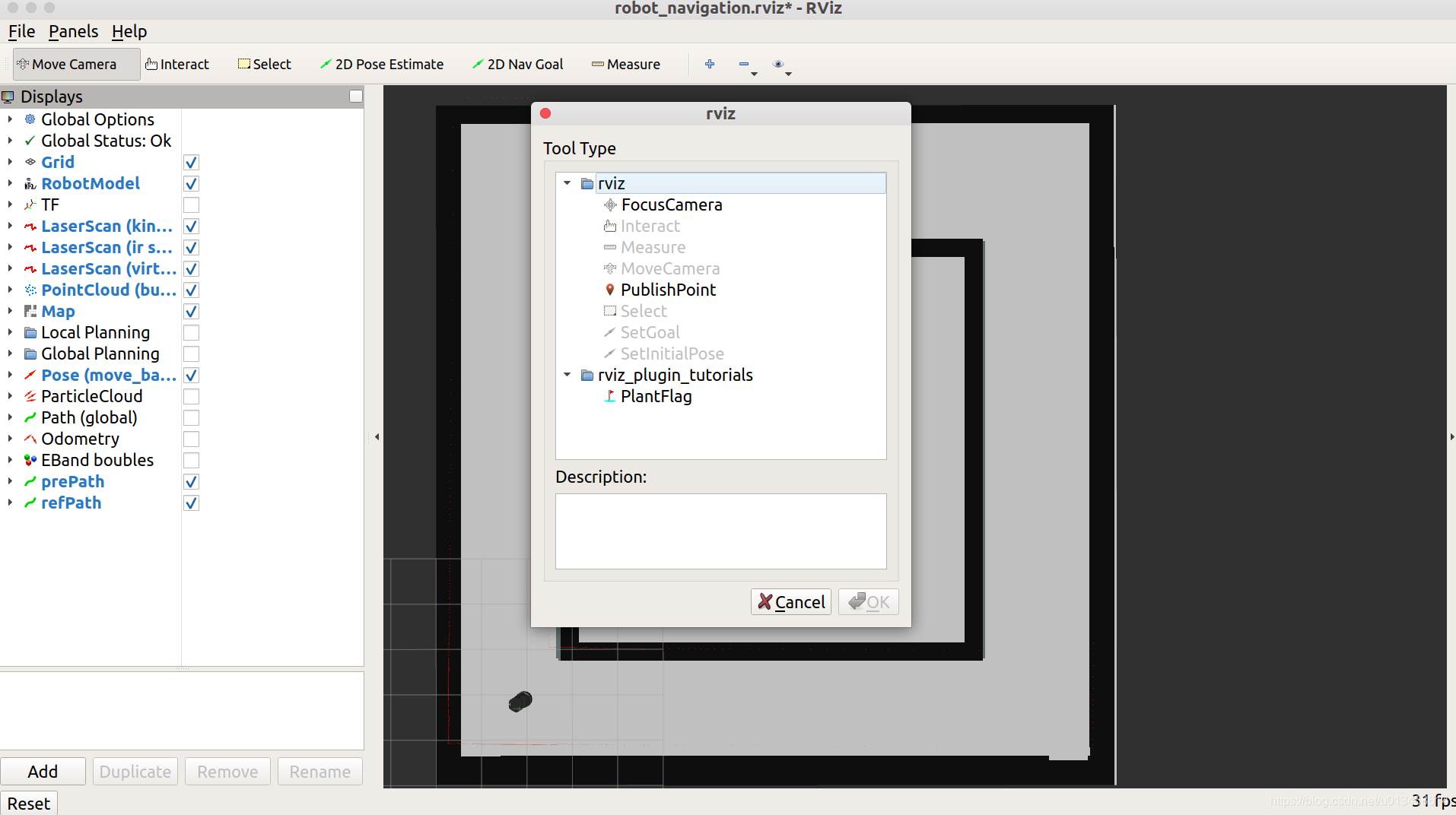

上面工具栏就会多出一个“Publish Point”，每点击一次该按钮，就可以在RVIZ界面中点击任意位置，并通过名称为“/clicked_point”的Topic发出该位置在“/map”坐标系下的位置（x,y）。

可采用如下程序来依次记录选取的路点（保存为“wps.txt”）：

import rospy
import numpy as np

from geometry_msgs.msg import PointStamped

class Turtlebot_core():
    def __init__(self):
        rospy.init_node("Turtlebot_core", anonymous=True)
        self.wps_buf = []
        
        rospy.Subscriber("/clicked_point", PointStamped, self.wpsCallback, queue_size=1)
        rospy.spin()            
            
    def wpsCallback(self, data):
        p1 = np.zeros(2)
        p1[0] = data.point.x
        p1[1] = data.point.y
        self.wps_buf.append(p1)
        np.savetxt("wps.txt", np.array(self.wps_buf))
        print("save way point success!!!")
        print("p:"+str(p1))
        

        
if __name__ == "__main__":
    turtlebot_core = Turtlebot_core()   

wps.txt文件内容如下

2.775404453277587891e+00 1.849611759185791016e+00
3.828148126602172852e+00 1.734118461608886719e+00
5.651257514953613281e+00 1.688370704650878906e+00
7.475209712982177734e+00 1.680246791839599609e+00
9.300391197204589844e+00 1.697043418884277344e+00
1.103435707092285156e+01 1.695110073089599609e+00
1.266803169250488281e+01 1.93492584228515625e+00
1.315559005737304688e+01 3.573270320892333984e+00
1.319308471679687500e+01 5.110162258148193359e+00
1.324398708343505859e+01 6.808045387268066406e+00
1.320587062835693359e+01 8.812158584594726562e+00
1.317775154113769531e+01 1.039849281311035156e+01
1.308286705017089844e+01 1.215956592559814453e+01
1.269116973876953125e+01 1.304349098205566406e+01
1.132855510711669922e+01 1.330544090270996094e+01
1.001482582092285156e+01 1.338727951049804688e+01
8.556406974792480469e+00 1.343830871582031250e+01
6.953704357147216797e+00 1.346025466918945312e+01
5.448281288146972656e+00 1.340069961547851562e+01
3.750601768493652344e+00 1.338894081115722656e+01
2.197587871551513672e+00 1.309178924560546875e+01
1.648979549407958984e+00 1.113714027404785156e+01
1.638838768005371094e+00 8.914575576782226562e+00
1.582886219024658203e+00 6.895450115203857422e+00
1.609868049621582031e+00 5.023091793060302734e+00
1.697061538696289062e+00 2.892292022705078125e+00
2.775404453277587891e+00 1.849611759185791016e+00

1.2.2 拟合路点得到机器人要跟踪的路线

import numpy as np
from scipy.interpolate import interp1d
wps = np.loadtxt("wps.txt")
x = wps[:,0]
y = wps[:,1]
t = np.linspace(0, 1, num=len(x))
f1 = interp1d(t,x,kind='cubic')
f2 = interp1d(t,y,kind='cubic')
newt = np.linspace(0,1,100)
newx = f1(newt)
newy = f2(newt)


import matplotlib.pyplot as plt
%matplotlib inline

plt.scatter(x, y)
plt.plot(newx, newy)
plt.show()

2. Turtlebot的MPC轨迹跟踪问题

与无人车不同，Turtlebot是基于左右轮差速来达到转弯，前行运动的。ROS中的Turtlebot包中的控制项有线速度v 与角速度w 。Turtlebot的运动学模型如下：

首先我们需要将以上连续的微分模型离散化成差分模型(差分间隔为d t） 

其中，cte \text{cte}cte与epsi \text{epsi}epsi的计算法公式详见无人车系统（十一）：轨迹跟踪模型预测控制(MPC)原理与python实现【40行代码】。
对于一个预测步长为$N$的MPC控制器求解问题，可以设计以下优化目标函数：

满足动态模型约束：

执行器约束:

3. 程序与运行结果

import rospy
import copy
import tf
import numpy as np
from scipy import spatial
from geometry_msgs.msg import PointStamped
from geometry_msgs.msg import PoseStamped
from nav_msgs.msg import Odometry
from nav_msgs.msg import Path
from geometry_msgs.msg import Twist
from pyomo.environ import *
from pyomo.dae import *
from scipy.interpolate import interp1d
import matplotlib
import matplotlib.pyplot as plt
%matplotlib inline
# set up matplotlib
is_ipython = 'inline' in matplotlib.get_backend()
if is_ipython:
    from IPython import display

plt.ion()

wps = np.loadtxt("wps.txt")
x = wps[:,0]
y = wps[:,1]
t = np.linspace(0, 1, num=len(x))
f1 = interp1d(t,x,kind='cubic')
f2 = interp1d(t,y,kind='cubic')
newt = np.linspace(0,1,100)
nwps = np.zeros((100, 2))
nwps[:,0] = f1(newt)
nwps[:,1] = f2(newt)
wpstree = spatial.KDTree(nwps)

def getcwps(rp):
    _, nindex = wpstree.query(rp)
    cwps = np.zeros((5,2))
    for i in range(5):
        cwps[i] = nwps[(nindex+i)%len(nwps)]
        
#     if (nindex + 5) >= 100:
#         cwps[0:100-nindex-1] = nwps[nindex:-1]
#         cwps[100-nindex-1:-1] = nwps[0:nindex+5-100]        
#     else:
#         cwps = nwps[nindex:nindex+5]
    return cwps    

def cubic_fun(coeffs, x):
    return coeffs[0]*x**3+coeffs[1]*x**2+coeffs[2]*x+coeffs[3]    
        
def plot_durations(cwps, prex, prey):
    plt.figure(2)
    plt.clf()
    plt.plot(cwps[:,0],cwps[:,1])
    plt.plot(prex, prey)
    plt.scatter(x, y)
    if is_ipython:
        display.clear_output(wait=True)
        display.display(plt.gcf())
 
        
        
N = 19 # forward predict steps
ns = 5  # state numbers / here: 1: x, 2: y, 3: psi, 4: cte, 5: epsi
na = 2  # actuator numbers /here: 1: steering angle, 2: omega


class MPC(object):
    def __init__(self):
        m = ConcreteModel()
        m.sk = RangeSet(0, N-1)
        m.uk = RangeSet(0, N-2)
        m.uk1 = RangeSet(0, N-3)
        
        m.wg       = Param(RangeSet(0, 3), initialize={0:1., 1:10., 2:100., 3:1000}, mutable=True) 
        m.dt       = Param(initialize=0.1, mutable=True)
        m.ref_v    = Param(initialize=0.5, mutable=True)
        m.ref_cte  = Param(initialize=0.0, mutable=True)
        m.ref_epsi = Param(initialize=0.0, mutable=True)
        m.s0       = Param(RangeSet(0, ns-1), initialize={0:0., 1:0., 2:0., 3:0., 4:0.}, mutable=True)
        m.coeffs   = Param(RangeSet(0, 3), 
                          initialize={0:-0.000458316, 1:0.00734257, 2:0.0538795, 3:0.080728}, mutable=True)
        
        
        m.s      = Var(RangeSet(0, ns-1), m.sk)
        m.f      = Var(m.sk)
        m.psides = Var(m.sk)
        m.uv     = Var(m.uk, bounds=(-0.01, 2.0))
        m.uw     = Var(m.uk, bounds=(-1.5, 1.5))
        
        # 0: x, 1: y, 2: psi, 3: cte, 4: epsi
        m.s0_update      = Constraint(RangeSet(0, ns-1), rule = lambda m, i: m.s[i,0] == m.s0[i])
        m.x_update       = Constraint(m.sk, rule=lambda m, k: 
                                      m.s[0,k+1]==m.s[0,k]+m.uv[k]*cos(m.s[2,k])*m.dt 
                                      if k<N-1 else Constraint.Skip)
        m.y_update       = Constraint(m.sk, rule=lambda m, k: 
                                      m.s[1,k+1]==m.s[1,k]+m.uv[k]*sin(m.s[2,k])*m.dt 
                                      if k<N-1 else Constraint.Skip)
        m.psi_update     = Constraint(m.sk, rule=lambda m, k: 
                                       m.s[2,k+1]==m.s[2,k]+ m.uw[k]*m.dt 
                                       if k<N-1 else Constraint.Skip)     
        m.f_update      = Constraint(m.sk, rule=lambda m, k: 
                                       m.f[k]==m.coeffs[0]*m.s[0,k]**3+m.coeffs[1]*m.s[0,k]**2+
                                       m.coeffs[2]*m.s[0,k]+m.coeffs[3])
        m.psides_update = Constraint(m.sk, rule=lambda m, k: 
                                           m.psides[k]==atan(3*m.coeffs[0]*m.s[0,k]**2
                                                              +2*m.coeffs[1]*m.s[0,k]+m.coeffs[2]))
        m.cte_update     = Constraint(m.sk, rule=lambda m, k: 
                                        m.s[3,k+1]==(m.f[k]-m.s[1,k]+m.uv[k]*sin(m.s[2,k])*m.dt) 
                                       if k<N-1 else Constraint.Skip)

        m.epsi_update    = Constraint(m.sk, rule=lambda m, k: 
                                   m.s[4, k+1]==m.psides[k]-m.s[2,k]+m.uw[k]*m.dt 
                                        if k<N-1 else Constraint.Skip)  
        
        m.cteobj  = m.wg[3]*sum((m.s[3,k]-m.ref_cte)**2 for k in m.sk)
        m.epsiobj = m.wg[3]*sum((m.s[4,k]-m.ref_epsi)**2 for k in m.sk)
        m.vobj    = m.wg[2]*sum((m.uv[k]-0.5)**2 for k in m.uk)
        m.uvobj   = m.wg[1]*sum(m.uv[k]**2 for k in m.uk)
        m.uwobj   = m.wg[1]*sum(m.uw[k]**2 for k in m.uk)
        m.sudobj  = m.wg[0]*sum((m.uv[k+1]-m.uv[k])**2 for k in m.uk1)
        m.suaobj  = m.wg[0]*sum((m.uw[k+1]-m.uw[k])**2 for k in m.uk1) 
        m.obj = Objective(expr = m.cteobj+m.epsiobj+m.vobj+m.uvobj+m.uwobj+m.sudobj+m.suaobj, sense=minimize)
        
        self.iN = m#.create_instance()
        
    def Solve(self, state, coeffs):        
        self.iN.s0.reconstruct({0:state[0], 1: state[1], 2:state[2], 3:state[3], 4:state[4]})
        self.iN.coeffs.reconstruct({0:coeffs[0], 1:coeffs[1], 2:coeffs[2], 3:coeffs[3]})
        self.iN.f_update.reconstruct()
        self.iN.s0_update.reconstruct()
        self.iN.psides_update.reconstruct()
        SolverFactory('ipopt').solve(self.iN)
        x_pred_vals = [self.iN.s[0,k]() for k in self.iN.sk]
        y_pred_vals = [self.iN.s[1,k]() for k in self.iN.sk]
        pre_path = np.zeros((N,2))
        pre_path[:,0] = np.array(x_pred_vals)
        pre_path[:,1] = np.array(y_pred_vals)        
        v = self.iN.uv[0]()
        w = self.iN.uw[0]()                                     
        return pre_path, v, w      
        
        
class Turtlebot_core():
    def __init__(self):
        rospy.init_node("Turtlebot_core", anonymous=True)
        self.listener = tf.TransformListener()
        rospy.Subscriber("/odom", Odometry, self.odomCallback)
        self.pub_refpath = rospy.Publisher("/ref_path", Path, queue_size=1)
        self.pub_prepath = rospy.Publisher("/pre_path", Path, queue_size=1)
        self.pub_cmd = rospy.Publisher("/cmd_vel_mux/input/teleop", Twist, queue_size=1)
        self.rp = np.zeros(3) 
        self.crv = 0.0
        self.crw = 0.0
        self.mpc = MPC() 
        rate = rospy.Rate(10) # 10HZ
        while not rospy.is_shutdown():
            self.getrobotpose()
            cwps = getcwps(self.rp[0:2])
            px = self.rp[0] + self.crv*np.cos(self.rp[2])*0.1
            py = self.rp[1] + self.crw*np.sin(self.rp[2])*0.1
            psi = self.rp[2] + self.crw*0.1
            
            self.rp[0] = px
            self.rp[1] = py
            self.rp[2] = psi
            
            cwps_robot = np.zeros((len(cwps), 2))
            
            for i in range(len(cwps)):
                dx = cwps[i,0] - px
                dy = cwps[i,1] - py
                
                cwps_robot[i,0] = dx*np.cos(psi) + dy*np.sin(psi)
                cwps_robot[i,1] = dy*np.cos(psi) - dx*np.sin(psi)
                
            coeffs = np.polyfit(cwps_robot[:,0], cwps_robot[:,1], 3)
            cte = cubic_fun(coeffs, 0)
            
            f_prime_x = coeffs[2]
            epsi = np.arctan(f_prime_x)
            s0 = np.array([0.0, 0.0, 0.0, cte, epsi])
            pre_path, v, w = self.mpc.Solve(s0, coeffs)
            self.pub_ref_path(cwps_robot)
            self.pub_pre_path(pre_path)
            self.pub_Command(v, w)
            print(v,w)
#             plot_durations(cwps, x_pred_vals, y_pred_vals)
            rate.sleep()        
        rospy.spin()            
            
    def getrobotpose(self):
        try:
            (trans,rot) = self.listener.lookupTransform('/map', '/base_link', rospy.Time(0))
        except (tf.LookupException, tf.ConnectivityException, tf.ExtrapolationException):
            return   
        self.rp[0] = trans[0]
        self.rp[1] = trans[1]
        r,p,y = tf.transformations.euler_from_quaternion(rot)
        self.rp[2] = y
        
    def odomCallback(self, data):
        self.crv = data.twist.twist.linear.x
        self.crw = data.twist.twist.angular.z
        
    def pub_ref_path(self, ref_path):        
        msg_ref_path = Path()
        msg_ref_path.header.stamp = rospy.Time.now()
        msg_ref_path.header.frame_id = "base_link"
        for i in range(len(ref_path)):
            pose = PoseStamped()
            pose.pose.position.x = ref_path[i,0]
            pose.pose.position.y = ref_path[i,1]
            msg_ref_path.poses.append(copy.deepcopy(pose))
            
        self.pub_refpath.publish(msg_ref_path)
            
    def pub_pre_path(self, pre_path):
        msg_pre_path = Path()
        msg_pre_path.header.stamp = rospy.Time.now()
        msg_pre_path.header.frame_id = "base_link"
        for i in range(len(pre_path)):
            pose = PoseStamped()
            pose.pose.position.x = pre_path[i,0]
            pose.pose.position.y = pre_path[i,1]
            msg_pre_path.poses.append(copy.deepcopy(pose))    
        self.pub_prepath.publish(msg_pre_path)
        
    def pub_Command(self, v, w):
        twist = Twist()
        twist.linear.x = v
        twist.angular.z = w
        self.pub_cmd.publish(twist)     
                
if __name__ == "__main__":
    turtlebot_core = Turtlebot_core() 

结果如下图所示（绿线为预测的轨迹，红线为turtlebot要跟踪的轨迹）：

4. 写在后面

基于MPC的轨迹跟踪方法的效果与所设定的目标函数、目标函数的参数有很大的关系。本文最后的参数都是通过不断的试验得到的，最终turtlebot能够在回形走廊环境中跟踪上要跟踪的轨迹。

by Toby 2020-2-2
愿疫情早点结束！