旋转运动学
线速度和角速度
粒子在坐标系中 的平面做圆周运动,坐标为:
。
 对坐标求导得:
对坐标求导得:  (1) 其中
(1) 其中 ,这里的
和
的
是不同的,也用了两种字体区分,
是
。
是旋转角对时间求导
的系数。
是我们定义的一个反对称矩阵。 对公式(1)两边取模得:
(
即
),这也是熟悉的线速度等于角速度×半径,隐含一个矢量关系,线速度方向是垂直于角速度和半径方向构成的平面的。
考虑一个更复杂的情况
 一起做一个实验,拿出一张白纸,尺子竖直放置在白纸上方(尺子不要移动),将白纸逆时针旋转(旋转轴与纸面的交点始终不要移动保持在尺子上)沿着尺子从交点划线,观察是否与上图中曲线相似。 下面进行推导: 质量块在 body 坐标系下的坐标为:
一起做一个实验,拿出一张白纸,尺子竖直放置在白纸上方(尺子不要移动),将白纸逆时针旋转(旋转轴与纸面的交点始终不要移动保持在尺子上)沿着尺子从交点划线,观察是否与上图中曲线相似。 下面进行推导: 质量块在 body 坐标系下的坐标为: ,上标表示坐标系。
 忽略平移,只考虑旋转,则旋转到惯性系下有:
忽略平移,只考虑旋转,则旋转到惯性系下有: (
是 base 到 inertial 系的旋转变换 )。 对时间求导有:

其中 ,表示 body 坐标系的角速度在
系下的表示。从
后面的式子可以看出 body 系下的线速度不仅受到 inertial 系的线速度的影响,同时受到角速度
的影响。 补充:
 这里对
这里对 的右乘扰动(可以用SO3来理解)
是角轴形式,
是一个时间小量,
与其相乘得到旋转角为模、旋转轴为方向的矢量。这里用到了伴随性质(
以及
)。 对速度求导得:
 (4) 同样做一个解释:
(4) 同样做一个解释: 这个东东是0,
矢量方向相同、叉乘为0。
直接把上式(2)移过来了。其中,
,
,
。表示物体在 body 下的速度、加速度或角速度在
系下的表示。 对式子做一个直观的解释:等号左边☜
是旋转坐标系 body 下的对旋转体系中进行加速度在
系下的表示,等号右边☞
是
静止坐标系下的加速度(大白话来说,就是
是先在 body 系下求加速度再用
转换到 inertial 系下,
是先用
把位移
转换到 inertial 系下,再通过求导得到的 inertial 系的加速度),欧拉力就是角加速度和半径之积(这个应该高中就学过)。 在旋转坐标系下观察,运动的物体(运动方向和旋转轴不为同一个轴时)会受到 科氏力的作用。
IMU 测量模型及运动模型
MEMS 加速度计工作原理
- 测量原理可以用一个简单的质量块 + 弹簧 + 指示计来表示。
- 加速度计测量值
为弹簧拉力对应的加速度,
(5)。
弹簧拉力,
物体在惯性系下的加速度,
重力加速度。
- MEMS 加速度计利用电容或者电阻桥等原理测量
。
- 东北天坐标系(ENU):
,
是什么就不用多说了吧……
- 假设 IMU 坐标系就是 ENU 坐标系,
(没有旋转,是单位阵),静止时有
;自由落体时有
。虽然材料上是这么写的,但是自由落体这个我没有想清楚,不是很认同。考虑到加速度的方向性,天U是正方向,
(由除重力加速度以外其他外力产生的加速度)就不能描述为自由落体。
MEMS 陀螺工作原理
- 陀螺仪主要用来测量物体的旋转角速度,按测量原理分为振动陀螺,光纤陀螺等。
- 低端 MEMS 陀螺上一般采用振动陀螺原理,通过测量 Coriolis force 来间接得到角速度。
- 在旋转坐标系中,运动的物体受到科氏力作用
。
- MEMS 陀螺仪:一个主动运动轴 + 一个敏感轴。 科氏力可以用电容或电阻桥等测出来,比如说:因为受科氏力(
)的作用使得质量块靠近电容的一个电极那么就可以用电压的变化量化这个科氏力。
音叉振动陀螺原理
- 叉子的中间为旋转轴,叉子左右两个质量块,做方向相反的正弦运动,质量块受到的科氏力方向相反。振动陀螺:两个质量块做在同一时间方向相反的正弦谐振运动。
- 由于质量块的运动方向相反,科氏力的方向也相反,如果质量块还受到外力影响,那么左右两个质量块会受到一个相同方向的力。我们使用相减的方式抵消外力影响,得到两倍的科氏力
。
陀螺仪的 G-sensitivity
实际上,两个质量块加工的时候不可能完全一致,也就是说陀螺仪的测量可能会受到外部加速度的影响,即称作 G-sensitivity。
IMU 误差模型
误差分类
- 加速度计和陀螺仪的误差可以分为:确定性误差,随机误差。
- 确定性误差可以事先标定确定,包括:bias,scale…
- 随机误差通常假设噪声服从高斯分布,包括:高斯白噪声,bias随机游走…
确定性误差
Bias:理论上,当没有外部作用时,IMU 传感器的输出应该为0。但是,实际数据存在一个偏置 。加速度计 bias 对位姿估计的影响:
,
。
 Scale:scale 可以看成是实际数值和传感器输出值之间的比值(电信号
Scale:scale 可以看成是实际数值和传感器输出值之间的比值(电信号 模拟信号,单位不同会通过一个 scale 的转化,这个 scale 会存在误差)。 Nonorthogonality/Misalignment Errors:多轴 IMU 传感器制作的时候,由于制作工艺的问题,会使得
轴可能不垂直。
 scale + Misalignment:
scale + Misalignment:  即每个轴都会受到尺度 scale 以及其他两个轴的分量影响:
即每个轴都会受到尺度 scale 以及其他两个轴的分量影响: 。
其他确定性误差
- Run-to-Run Bias/Scale Factor
- In Run (Stability) Bias/Scale Factor
- Temperature-Dependent Bias/Scale Factor
- …
六面法标定加速度 bias 和 scale factor
六面法是指将加速度计的 3 个轴分别朝上或者朝下水平放置一段时间,采集 6 个面的数据完成标定。玩过无人机的同学应该了解,无人机Pixhawk飞控就要这么捣鼓一下,我当时拿着八轴ZD850的无人机硬生生的翻来翻去。 如果各个轴都是正交的,那很容易得到 bias 和 scale: 
其中, 为加速度计某个轴的测量值,
为当地的重力加速度。 例:z轴朝上
,z轴朝下
,那么误差
就是
。 考虑轴间误差时,实际加速度和测量值之间的关系为:
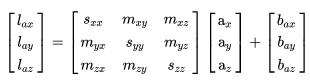 (7) 水平静止放置 6 面时,加速度的理论值为:
(7) 水平静止放置 6 面时,加速度的理论值为:
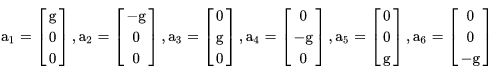
对应的测量矩阵
。用最小二乘法就可以把
和
12个变量求出来。这其实就是标定的过程,即确定每个轴加速度计算式(理论值
测量值)的各项系数准确。
六面法标定陀螺仪 bias 和 scale factor
和加速度计六面法不同的是,陀螺仪的真实值由高精度转台提供,这里的 6 面是指各个轴顺时针和逆时针旋转。除此之外其他的与六面法标定加速度相似。
温度相关的参数标定
- 目的:这个标定的主要目的是对传感器估计的 bias 和 scale 进行温度补偿,获取不同温度时 bias 和 scale 的值,绘制成曲线。
两种标定方法:
- soak method:控制恒温室的温度值,然后读取传感器数值进行标定。
- ramp method:记录一段时间内线性升温和降温时传感器的数据来进行标定。
IMU 随机误差
高斯白噪声
IMU 数据连续时间上受到一个均值为0,方差为 ,各时刻之间相互独立的高斯过程
:
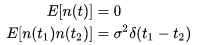
(8) 其中 表示狄拉克函数(
时为1,学过《信号与系统》的同学应该再熟悉不过了),用来表征高斯白噪声的独立性。
Bias 随机游走
通常用维纳过程(wiener process)来建模 bias 随时间连续变化的过程,离散时间下称之为随机游走。
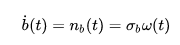
(9) 其中 是方差为 1 的白噪声。 前面我们都是在连续时间下进行建模的,而 IMU 获取的数据是离散采样,连续高斯白噪声和离散存在哪种关系呢? 假设有一个单轴角速度信号收到高斯白噪声和 bias 的影响,建模如下:

是理想的,
是测量的。 当传感器采集信号时,假设采样时间段内信息为常数:
 (11) 即
(11) 即  (12) 首先只考虑高斯白噪声的积分
(12) 首先只考虑高斯白噪声的积分  (13)
(13)  协方差为
协方差为  (14) 二次积分是求出了这个时间段内,每个时刻之间的协方差,均值为0也就是说高斯白噪声的连续时间到离散时间之间差一个 , 是传感器的采样时间。 。只有当
(14) 二次积分是求出了这个时间段内,每个时刻之间的协方差,均值为0也就是说高斯白噪声的连续时间到离散时间之间差一个 , 是传感器的采样时间。 。只有当 和
是同一时刻时狄拉克函数
,
。后对
求一次积分为 1 ,1 再求一次积分为
。 即
![]() (15) 其中
(15) 其中  (16)
(16)
也就是说高斯白噪声的连续时间到离散时间之间差一个
,
是传感器的采样时间。
这里同样是计算不同时刻之间的协方差。 由于 有:
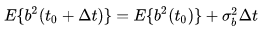
(19) 是因为这次无
。 即:
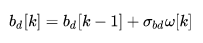
(20) 其中:
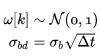
(21)
bias 随机游走的噪声方差从连续时间到离散之间需要乘以
。
更详细的推导参见[2]。
IMU 随机误差的标定
艾伦方差标定 random walk noise
Allan 方差法是 20 世纪 60 年代由美国国家标准局的 David Allan 提出的,是一种基于时域的分析方法。 具体的流程如下:
- 保持传感器绝对静止获取数据 2 小时以上。
- 对数据进行分段,设定时间段的时长,如下图所示,图中假设一次采样时间为
,段长为
。
- 将传感器数据按照时间段进行平均。
- 计算方差,绘制艾伦曲线。
 艾伦曲线↓
艾伦曲线↓  图中,
图中, 与横轴
的交点就是高斯白噪声的不确定度;
与横轴
的交点就是 bias 随机游走的不确定度。 为什么是这样呢?可以查看注释链接的论文。
加速度计数学模型
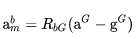
(22) 如果考虑高斯白噪声,bias,以及尺度因子(电信号
),则为:
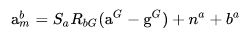 (23)
(23)
通常假设尺度因子为单位矩阵。
陀螺仪数学模型
考虑高斯白噪声,bias,以及尺度因子,陀螺仪的误差模型如下:
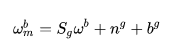 (24)
(24)
低端传感器,考虑加速度对陀螺仪的影响,即 g-灵敏度:
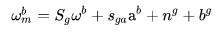 (25)
(25)
运动模型离散时间处理
连续时间下 IMU 运动模型
忽略 scale 的影响,只考虑白噪声和 bias 随机游走:
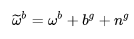 (26)
(26)
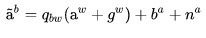 (27)
(27)
上标 表示 gyro(陀螺仪gyroscope),
表示 acc(加速度计accelerometer),
表示世界坐标系 world,
表示 imu 机体坐标系 body。IMU 的真实值为
,测量值为
。 P(ose),V(elocity),Q(uaternion)对时间导数可写成:

(28)
根据导数关系,可以从第 i 时刻的 PVQ,通过对 IMU 的测量值进行积分,得到第 j 时刻的 PVQ: 
(29)
运动模型的离散积分——欧拉法
使用欧拉法,即两个相邻时刻 k 到 k+1 的位姿是用第 k 时刻的测量值 来计算。

(30)
其中,
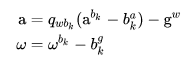 (31)
(31)
连续时间下,四元数的更新是用 对
的积分确定的,至于四元数在时间上的导数
在上一章解释过,这里不做过多解释。而离散时间下,四元数的更新是用
也就是
在
很小时的一个趋近值。

(32)
运动模型的离散积分——中值法
即两个相邻时刻 k 到 k+1 的位姿是用两个时刻的测量值 的平均值来计算。

(32)
上面公式和(30)相同,但是其中,
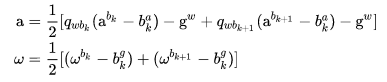 (33)
(33)
旋转基础知识
旋转积分的几种形式
(34)
SO3 形式:
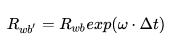 (35)
(35)
欧拉角形式:
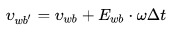 (36)
(36)
其中 ,
表示将 IMU body 坐标系下的角速度转换成欧拉角速度。 如何从惯性坐标系的坐标转换到 body 坐标系下? step 1. 绕着惯性坐标系的 z 轴旋转,得到新的坐标系
。
 step 2. 绕着新坐标系
step 2. 绕着新坐标系 的 y 轴旋转得到坐标系
。
 step 3. 绕着坐标系
step 3. 绕着坐标系 的 x 轴旋转得到坐标系
,它就是 body 坐标系。
 综合起来,得到:
综合起来,得到:  欧拉角速度转换到 body 坐标系下? 因为最后绕 x 轴旋转,所以 x 轴对应的旋转角
欧拉角速度转换到 body 坐标系下? 因为最后绕 x 轴旋转,所以 x 轴对应的旋转角 不需要改变。而绕 y 轴的旋转角
需要经过
的变换才会在 body 系下,绕 z 轴的旋转角
则需要经过
的变换。 故:

(37)
去逆就得到,body rate to euler rate 的变换: 
参考
- ^科氏力(科里奥利力) https://baike.baidu.com/item/%E7%A7%91%E9%87%8C%E5%A5%A5%E5%88%A9%E5%8A%9B/1255543?fromtitle=%E7%A7%91%E6%B0%8F%E5%8A%9B&fromid=9085076&fr=aladdin
- ^Crassidis, J. L . Sigma-point Kalman filtering for integrated GPS and inertial navigation[J]. Aerospace & Electronic Systems IEEE Transactions on, 2006, 42(2):750-756. https://xueshu.baidu.com/usercenter/paper/show?paperid=319f9bbcd890e2998e4b9d300d82f37f&site=xueshu_se
- ^Allan Variance. “Noise Analysis for Gyroscopes”. In: Freescale Semiconductor Document Number: AN5087 Application Note Rev. 0 2 (2015). https://www.nxp.com/docs/en/application-note/AN5087.pdf
- ^MA Shelley. “Monocular visual inertial odometry on a mobile device”. https://xueshu.baidu.com/usercenter/paper/show?paperid=68dda4a4688ea361c151eab22dedbe17&site=xueshu_se
- ^MIT. Kinematics Of Moving Frames. https://ocw.mit.edu/courses/mechanical-engineering/2-017j-design-of-electromechanical-robotic-systems-fall-2009/course-text/MIT2_017JF09_ch09.pdf















