三、机器人运动学

从机械的角度看，一个机械手可以用一系列通过转动关节或移动关节连接的刚体（连杆）运动链进行概要表示。链的一端安装在基座上，末端执行器则安装在链的另一端。链结构的运动结果可以通过每一连杆相对前一连杆的基本运动合成得到。因而，为了在空间中操作目标，有必要描述出末端执行器的位置和方向。本节基于线性代数知识，通过系统而一般性的方法，推导得出正运动学方程（direct kinematics equation），使末端执行器的位置和方向（简称为位姿）可以表示为相对参考坐标系机械结构中关节变量的函数。其中开链和闭链运动学结构都将考虑。为获得方向的最简表示（minimal representation of orientation），本节将介绍操作空间（operational space）的概念，并建立其与关节空间（joint space）的关系。

3.1 刚体的姿态

刚体（rigid body）可以由其在空间中相对参考坐标系的位置和方向（简记为位姿）进行完整的描述。如图所示，令 $O-xyz$ 为标准正交参考坐标系， $x,y,z$ 为坐标轴的单位向量。

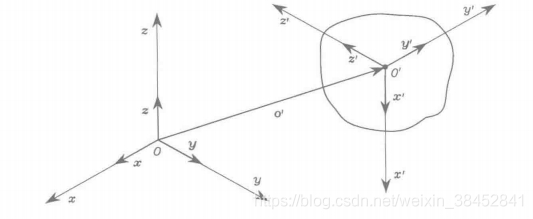
图3.1 刚体的位置和方向

刚体上的点 $O^{'’}$ 相对坐标系 $O-xyz$ 的位置可以表示为关系式

$o^{'}=o_{x}^{'}x+o_{y}^{'}y+o_{z}^{'}x$

其中， $o_{x}^{'},o_{y}^{'},o_{z}^{'}$ 表示向量 $o^{'}\in\mathbb{R}^{3}$ 在坐标轴上的分量。 $O^{'’}$ 的位置可以简写为（ $3\times 1$ ）向量

$o^{'}=\begin{bmatrix} o_{x}^{'}\\\\ o_{y}^{'} \\\\ o_{z}^{'} \end{bmatrix}$ （3.1）

由于除了方向和模长，其作用点和作用线都是规定的，因此 $o^{'}$ 是有界向量。

为了描述刚体的指向，考虑建立一个固连于刚体的标准正交坐标系，并由其相对参考坐标系的单位向量来表示。令此坐标系为 $O-x^{'}y^{'}z^{'}$ 中的表达式为：

$x^{'}=x_{x}^{'}x+x_{y}^{'}y+x_{z}^{'}z$
$y^{'}=y_{x}^{'}x+y_{y}^{'}y+y_{z}^{'}z$ （3.2）

$z^{'}=z_{x}^{'}x+z_{y}^{'}y+z_{z}^{'}z$

每一单位向量的分量都是坐标系 $O^{'}-x^{'}y^{'}z^{'}$ 的轴相对参考坐标系 $O-xyz$ 的方向余弦。

3.2 旋转矩阵

为了描述简便起见，上式中描述刚体相对参考坐标系的指向的三个单位向量可以组合为一个（ $3\times 3$ ）矩阵。

$R=\begin{bmatrix} x^{'} & y^{'} &z^{'} \end{bmatrix}=\begin{bmatrix} x_{x}^{'} & y_{x}^{'} &z_{x}^{'} \\ \\ x_{y}^{'} & y_{y}^{'} & z_{y}^{'} \\ \\ x_{z}^{'} &y_{z}^{'} & z_{z}^{'} \end{bmatrix}=\begin{bmatrix} x^{'T}x& y^{'T}x & z^{'T}x \\ \\ x^{'T}y& y^{'T}y & z^{'T}y \\ \\ x^{'T}z & y^{'T}z & z^{'T}z \end{bmatrix}$ （3.3）

定义R为旋转矩阵。

需要注意矩阵R的列向量相互正交，原因在于它们表示的是正交坐标系的单位向量，即

$x^{'T}y^{'}=0$ $y^{'T}z^{'}=0$ $z^{'T}x^{'}=0$

同时，其模长均为1，即

$x^{'T}x^{'}=1$ $y^{'T}y^{'}=1$ $z^{'T}z^{'}=1$

因此，矩阵R是一个正交矩阵，即

$R^{T}R=I_{3}$ （3.4）

其中， $I_{3}$ 表示（ $3\times 3$ ）单位矩阵。

如果在上式的两边同时右乘逆矩阵 $R^{-1}$ ，可以得到以下有用的结论：

$R^{T}=R^{-1}$ （3.5）

即旋转矩阵的转置与其逆矩阵相等。进一步地，注意到如果坐标系满足右手法则，则det( $R$ )=1，如果满足左手法则，则det( $R$ )=-1。

如上定义的旋转矩阵属于实（ $m\times m$ ）矩阵中的特殊正交群（special orthonormal group） $SO\left ( m \right )$ ，其列为正交的且行列式为1。在作空间旋转时，m=3，在作平面旋转时，m=2。

3.2.1 基本旋转

考虑一个坐标系可以通过参考坐标系相对某一坐标轴的基本旋转得到。如果想对坐标轴作逆时针方向旋转，则旋转为正。

假设参考坐标系 $O-xyz$ 绕 $Z$ 轴旋转角度 $\alpha$ ，令 $O-x^{'}y^{'}z^{'}$ 为旋转后的坐标系。新坐标系的单位向量可以通过其相对参考坐标系的分量来描述。即

图3.2 坐标系 $O-xyz$ 绕坐标轴 $z$ 旋转 $\alpha$ 角

$x^{'}=\begin{bmatrix} cos\alpha \\ sin\alpha \\ 0 \end{bmatrix}$ $y^{'}=\begin{bmatrix} -sin\alpha \\ cos\alpha \\ 0 \end{bmatrix}$ $z^{'}=\begin{bmatrix} 0 \\ 0 \\ 1 \end{bmatrix}$

从而，坐标系 $O-x^{'}y^{'}z^{'}$ 关于坐标系 $O-xyz$ 的旋转矩阵为

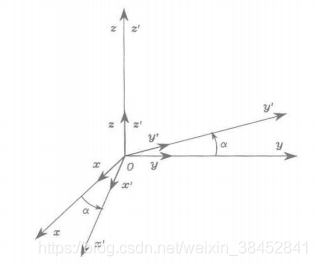
$R_{x}\left ( \alpha \right )=\begin{bmatrix} cos\alpha & -sin\alpha & 0\\ sin\alpha & cos\alpha & 0\\ 0 & 0 & 1 \end{bmatrix}$ （3.6）

类似的，绕 $y$ 轴旋转 $\beta$ 角及绕 $x$ 轴旋转 $\gamma$ 的旋转可以分别由下列式子给出

$R_{y}\left ( \beta \right )=\begin{bmatrix} cos\beta & 0& sin\beta \\ 0 & 1 & 0\\ -sin\beta & 0 & cos\beta \end{bmatrix}$ （3.7）

$R_{z}\left ( \gamma \right )=\begin{bmatrix} 1 & 0&0 \\ 0 & cos\gamma & -sin\gamma \\ 0 & sin\gamma & cos\gamma \end{bmatrix}$ （3.8）

这些矩阵将有助于描述绕空间中任一轴的旋转。

容易验证，上述几式中的基本旋转具有如下性质：

$R_{k}\left ( -\theta \right )=R_{k}^{T}\left ( \theta \right )$ $k=x,y,z$ （3.9）

考虑上式，旋转矩阵可以被赋予几何意义，即矩阵R描述了在空间中将参考坐标系的坐标轴调整到与机器人本体坐标系相应的坐标轴相一致时，所需要绕单个坐标轴进行的旋转。

3.2.2 向量的表示

为更深入理解旋转矩阵的几何含义，考虑本体坐标系原点与参考坐标系原点重合的情况（图3.3），此时， $o^{'}=0$ ，其中 $0$ 代表 $\left ( 3\times 1 \right )$ 零向量。

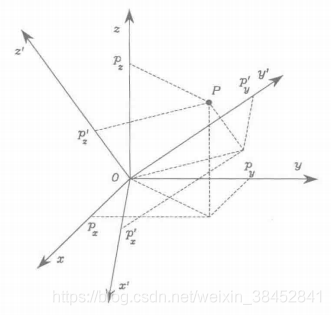
图3.3 点 $P$ 在两个不同坐标系中的表示

相对于坐标系 $O-xykz$ ，空间中的一点 $P$ 可以表示为

$p=\begin{bmatrix} p_{x}\\ p_{y}\\ p_{z} \end{bmatrix}$

或相对于坐标系 $O-x^{'}y^{'}z^{'}$ ，点 $P$ 可以表示为

$p=\begin{bmatrix} p_{x}^{'}\\ \\p_{y}^{'}\\\\ p_{z}^{'} \end{bmatrix}$

由于 $p$ 和 $p^{'}$ 表示的是同一点 $P$ ，有

而且，根据式（3.3），有

$p=Rp^{'}$ （3.10）

旋转矩阵 $R$ 表示坐标系 $O-x^{'}y^{'}z^{'}$ 中的向量坐标转换为同一向量在坐标系 $O-xyz$ 中的坐标的变换矩阵（transformation matrix）。由式（3.4）的正交性质，逆变换可简单地由下式给出

$p^{'}=R^{T}p$ （3.11）

3.2.3 向量的旋转

旋转矩阵也可视为使某一向量绕空间中任一轴旋转给定角度的矩阵算子。事实上，令 $p^{'}$ 为参考坐标系 $O-xyz$ 中的一个向量，由于矩阵 $R$ 的正交性，乘积 $Rp^{'}$ 得到的向量 $p$ 与 $p^{'}$ 的模相等，但是按照矩阵 $R$ 关于 $p^{'}$ 进行了旋转。模相等这一点可以通过 $p^{T}p=p^{'T}R^{T}Rp^{'}$ 并利用式（3.4）加以证明。后面还将对旋转矩阵的这一解释进行讨论。

3.3 旋转矩阵的合成

为了推导旋转矩阵的合成规则，有必要考虑一个向量在两个不同参考坐标系下的表示。因此，令 $O-x_{0}y_{0}z_{0}$ 、 $O-x_{1}y_{1}z_{1}$ 、 $O-x_{2}y_{2}z_{2}$ 为三个具有同一原点 $O$ 的坐标系。描述空间中任一点位置的向量 $p$ 可以在上述三个坐标系中进行表示。令 $p^{0},p^{1},p^{2}$ 分别代表向量 $p$ 在三个坐标系中的表示。

首先，考虑向量 $p$ 在坐标系2中的表达式 $p^{2}$ 与同一个向量在坐标系1中的表达式 $p^{1}$ 之间的关系。如果 $R_{i}^{j}$ 代表坐标系 $i$ 关于坐标系 $j$ 的旋转矩阵，有

$p^{1}=R_{2}^{2}p^{2}$ （3.12）

类似地，有

$p^{0}=R_{1}^{0}p^{1}$ （3.13）

$p^{0}=R_{2}^{0}p^{2}$ （3.14）

另一方面，将式（3.12）代入式（3.13），并利用式（3.14）得到

$R_{2}^{0}=R_{1}^{0}R_{2}^{1}$ （3.15）

式（3.15）中的矩阵关系可以解释为连续旋转的合成。考虑一个坐标系初始状态与坐标系 $O-x_{0}y_{0}z_{0}$ 一致。用矩阵 $R_{2}^{0}$ 表示的旋转可以看作是通过两步得到的：

首先根据 $R_{1}^{0}$ 对给定坐标系进行旋转，使之与坐标系 $O-x_{1}y_{1}z_{1}$ 一致。
然后根据 $R_{2}^{1}$ 将现在已与坐标系 $O-x_{1}y_{1}z_{1}$ 一致的坐标系进行旋转，使之与坐标系 $O-x_{2}y_{2}z_{2}$ 一致。

注意到完整的旋转可以表示成一系列的部分旋转，每一个部分旋转均相对前一个旋转进行定义，进行旋转的参考坐标系定义为当前坐标系。从而按给定的旋转顺序右乘旋转矩阵，进行连续旋转的合成，如式（3.15）。采用式（3.5）中的记法，有

$R_{i}^{j}=R_{j}^{i}^{-1}=R_{j}^{i}^{T}$ （3.16）

连续旋转也可以一直相对初始坐标系来进行解释。在此情形下，旋转是相对固定坐标系进行的。令 $R_{1}^{0}$ 为坐标系 $O-x_{1}y_{1}z_{1}$ 关于固定坐标系 $O-x_{0}y_{0}z_{0}$ 的旋转矩阵，然后令 $\bar{R_{2}^{0}}$ 表征坐标系 $O-x_{2}y_{2}z_{2}$ 相对坐标系0的矩阵关系，它由坐标系1根据矩阵 $\bar{R_{2}^{1}}$ 进行旋转得到。由于（3.15）式给出了绕当前坐标系的轴进行连续旋转的合成规则，整体旋转可以被看作是通过以下步骤得到的：

首先用坐标系0通过旋转 $R_{1}^{0}$ 对坐标系1进行重排。
然后，将当前坐标系的旋转表示为 $\bar{R_{2}^{1}}$ 。
最后，通过逆旋转 $R_{1}^{0}$ 补偿重排坐标系进行的旋转。

由于上述旋转是关于当前坐标系进行描述的，应用式（3.15）的合成规则可得

$\bar{R_{2}^{0}}=R_{1}^{0}R_{0}^{1}\bar{R_{2}^{1}}R_{1}^{0}$

考虑式（3.16），有

$\bar{R_{2}^{0}}=\bar{R_{2}^{1}}R_{1}^{0}$ （3.17）

其中，得到的 $\bar{R_{2}^{0}}$ 不同于式（3.15）中的矩阵 $R_{2}^{0}$ 。由此可知，关于固定坐标系连续旋转的合成，可以通过按照给定的旋转顺序，左乘单个旋转矩阵进行。

回顾旋转矩阵在当前坐标系相对固定坐标系的指向方面的含义，可以意识到，旋转矩阵的列为当前坐标系的轴相对固定坐标系的方向余弦，而其行（其转置矩阵和逆矩阵的列）则为固定坐标系的轴关于当前坐标系的方向余弦。

旋转合成中的一个重要问题，是矩阵乘法不满足交换律。考虑到这一点，可以得出这样的结论，即一般来说两个旋转不可交换顺序，并且其合成关系依赖于单个旋转的顺序。

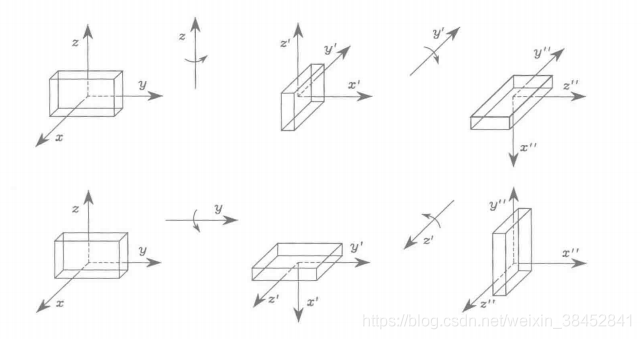
图3.6 物体绕当前坐标系的轴的相继旋转

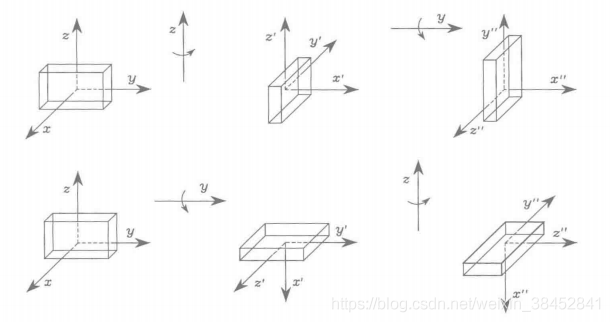
图3.7 物体绕固定坐标系的轴的连续旋转

3.4 欧拉角

旋转矩阵对于坐标系指向的描述是冗余的。旋转矩阵用了9个元素来刻画其特征，而事实上，由于式（3.4）给出的正交性条件带来6个约束，这9个元素之间不是独立的，而是相关的。这就意味着，只要3个参数就足以描述一个刚体在空间中的指向。由3个独立的参数对指向进行描述，构成最简表示式。事实上，特殊正交群 $SO\left ( m \right )$ 的最简表示需要 $\frac{m\left ( m-1 \right )}{2}$ 个参数，因此，需要用3个参数来表示 $SO\left ( 3 \right )$ ，而表示一个平面旋转 $SO\left ( 2 \right )$ 只需要一个参数。

指向的最简表示可以通过三个角度的集合 $\phi =\begin{bmatrix} \varphi &\theta & \psi \end{bmatrix}^{T}$ 得到。将表示绕一个坐标轴进行基本旋转的旋转矩阵看成是单个角度的函数。这样，一般的旋转矩阵就可以通过3个基本旋转的1个适当序列的合成来实现，在此过程中需要保证两个连续旋转不是绕平行轴进行的。这就意味着在27种可能的组合中，只有12种不同的角度集合是可行的，每一集合表示3个一组的欧拉角。下面，将对两组欧拉角进行分析，即 $ZYZ$ 和 $ZYX$ （或滚动-俯仰-偏航）角。

3.4.1 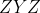$ZYZ$ 角

用 $ZYZ$ 角描述的旋转可以通过如下的基本旋转合成得到。

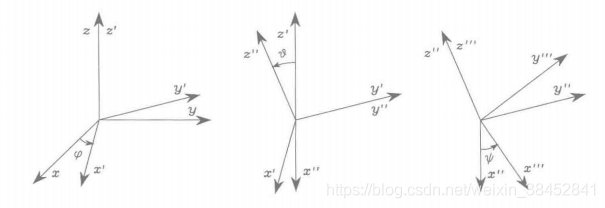
图3.8 欧拉角的 $ZYZ$ 表示

将参考坐标系绕 $z$ 轴旋转角度 $\varphi$ ，这一旋转可以用式（3.6）定义的矩阵 $R_{z}\left ( \varphi \right )$ 来描述。
将当前坐标系绕 $y^{'}$ 轴旋转角度 $\theta$ ，这一旋转可以用式（3.7）定义的矩阵 $R_{y^{'}}\left (\theta \right )$ 来描述。
将当前坐标系绕 $z^{''}$ 轴旋转角度 $\psi$ ，这一旋转同样可以用式（3.6）定义的矩阵 $R_{z^{''}}\left ( \psi \right )$ 来描述。

最终坐标系的指向通过相对当前坐标系旋转的合成得到，因此可以通过右乘基本旋转矩阵来计算，即 $R\left ( \phi \right )=R_{z}\left ( \varphi \right )R_{y^{'}}\left (\theta \right )R_{z^{''}}\left ( \psi \right )=\begin{bmatrix} c_{\varphi }c_{\theta }c_{\psi }-s_{\varphi }s_{\psi }& -c_{\varphi }c_{\theta }s_{\psi }-s_{\varphi }c_{\psi }& c_{\varphi }s_{\theta }\\ s_{\varphi }c_{\theta }c_{\psi }+c_{\varphi }s_{\psi }& -s_{\varphi }c_{\theta }s_{\psi }+c_{\varphi }c_{\psi }&s_{\varphi }s_{\theta } \\ -s_{\theta }c_{\psi } & s_{\theta }s_{\psi } & c_{\theta } \end{bmatrix}$ （3.18）

确定相应于给定旋转矩阵的欧拉角集合，对逆运动学问题求解很有用。假定旋转矩阵为

$R=\begin{bmatrix} r_{11} & r_{12}&r_{13} \\ r_{21}& r_{22} & r_{23}\\ r_{31}& r_{32} & r_{33 \end{bmatrix}$

将此表达式与式（3.18）中 $R\left ( \phi \right )$ 的表达式相比较。考虑元素 $\begin{bmatrix} 1 & 3 \end{bmatrix}$ 和 $\begin{bmatrix} 2 & 3 \end{bmatrix}$ ，假定 $r_{13}\neq 0$ 及 $r_{23}\neq 0$ ，有

$\varphi =Atan2(\left r_{23},r_{13} \right )$

其中， $Atan2\left ( y,x \right )$ 为两个自变量的反正切函数。然后，求元素 $\left [ 1,3 \right ]$ 和 $\left [ 2,3 \right ]$ 的平方和并利用元素 $\left [ 3,3 \right ]$ ，得到

$\varphi =Atan2\left (\sqrt{ r_{13}^{2}+ r_{23}^{2}},r_{33} \right )$

选择 $\sqrt{r_{13}^{2}+r_{23}^{2}}$ 项的系数为正，将 $\theta$ 的取值范围限定在 $\left ( 0,\pi \right )$ 。基于这样的假设，考虑元素 $\left [ 3,1 \right ]$ 和 $\left [ 3,2 \right ]$ ，有

$\varphi =Atan2\left ( r_{32},-r_{31} \right )$

故，所求解为

$\varphi =Atan2\left ( r_{32},-r_{31} \right )$

$\theta =Atan2\left (- r_{31},\sqrt{r_{32}^{2}+r_{33}^{2}} \right )$ （3.19）

$\psi =Atan2\left ( r_{32},r_{33} \right )$

也有可能得到其他的解，这些解与（3.19）式中的解效果是一样的。在 $\left ( -\pi ,0 \right )$ 中选择 $\theta$ 得到

$\varphi =Atan2\left (- r_{23},-r_{13} \right )$

$\varphi =Atan2\left (-\sqrt{ r_{13}^{2}+ r_{23}^{2}},r_{33} \right )$ （3.20）

$\varphi =Atan2\left ( -r_{32},r_{31} \right )$

当 $s_{\theta }$ =0时，解（3.19）、（3.20）会退化。在这种情形下，可能只能确定 $\varphi$ 和 $\psi$ 的和或差。事实上，如果 $\theta =0$ ， $\pi$ ，则连续的旋转 $\varphi$ 和 $\psi$ 是绕当前坐标系的平行轴进行的，这就使得旋转是等价的。

3.4.2 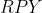$RPY$ 角

另一组欧拉角来源于（航空）航海领域方向的表示。这些是 $ZYX$ 角，也称为滚动-俯仰-偏航角，用来指示飞行器姿态的典型改变。在这种情形下，角 $\phi =\left | \varphi ,\theta ,\psi \right |^{T}$ 表示相对固连于飞行器质心的固定工坐标系定义的旋转。（图3.4）

按照滚动-俯仰-偏航角得到的旋转结果可以按照如下步骤获得：

将参考坐标系绕 $x$ 轴旋转角度 $\psi$ （偏航角），这一旋转由如（3.8）式定义的矩阵 $R_{x}\left ( \psi \right )$ 描述。
将参考坐标系绕 $y$ 轴旋转角度 $\theta$ （俯仰角），这一旋转由如（3.7）式定义的矩阵 $R_{y}\left ( \theta \right )$ 描述。
将参考坐标系绕 $z$ 轴旋转角度 $\varphi$ （滚动角），这一旋转由如（3.6）式定义的矩阵 $R_{z}\left ( \varphi \right )$ 描述。

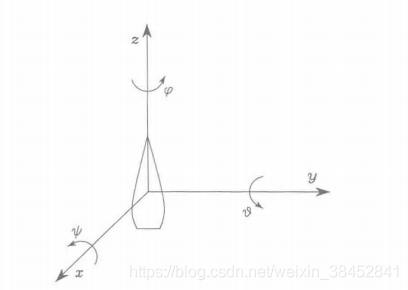
坐标系的最终指向由相对固定坐标系旋转的合成得到，因此可以通过左乘基本旋转矩阵计算得到，即 $R\left ( \phi \right )=R_{z}\left ( \varphi \right )R_{y}\left (\theta \right )R_{x}\left ( \psi \right )=\begin{bmatrix} c_{\varphi }c_{\theta }& c_{\varphi }s_{\theta }s_{\psi }-s_{\varphi }s_{\psi }& c_{\varphi }s_{\theta }c_{\psi }+s_{\varphi }s_{\psi }\\ s_{\varphi }c_{\theta }& s_{\varphi }s_{\theta }s_{\psi }+c_{\varphi }c_{\psi }&s_{\varphi }s_{\theta } c_{\psi }-c_{\varphi }s_{\psi} \\ -s_{\theta } & c_{\theta }s_{\psi } & c_{\theta }c_{\psi } \end{bmatrix}$ （3.21）

图3.9 滚动-俯仰-偏航角度的表示

而欧拉角 $ZYZ$ 是如下给定旋转矩阵的逆解

$R=\begin{bmatrix} r_{11} &r_{12} &r_{13} \\ r_{21} & r_{22} &r_{23}\\ r_{31}& r_{32} &r_{33} \end{bmatrix}$

可以通过将其与式（3.21）中 $R\left ( \phi \right )$ 的表达式相比较得到。

当 $\theta$ 属于区间 $\left (- \frac{\pi }{2},\frac{\pi }{2} \right )$ 时，有

$\varphi =Atan2\left ( r_{21},r_{11} \right )$

$\theta =Atan2\left (- r_{31},\sqrt{r_{32}^{2}+r_{33}^{2}} \right )$ （3.22）

$\psi =Atan2\left ( r_{32},r_{33} \right )$

当 $\theta$ 属于区间时 $\left (-\frac{\pi }{2},\frac{3\pi }{2} \right )$ 时，其等价的解为

$\varphi =Atan2\left (- r_{21},-r_{11} \right )$

$\theta =Atan2\left (- r_{31},\sqrt{r_{32}^{2}+r_{33}^{2}} \right )$ （3.23）

$\psi =Atan2\left ( -r_{32},-r_{33} \right )$

当 $c_{\theta }=0$ 时，得到（3.22）和（3.23）中的退化解。此时，有可能只能确定 $\varphi$ 和 $\psi$ 的和或差。

3.5 角和轴

绕空间中某一轴旋转指定角度的指向的非最简表达式，可以采用4个参数进行表示。这一点在机械手末端执行器指向的轨迹规划问题中是有用的。

令 $r=\begin{bmatrix} r_{x} & r_{y} & r_{z} \end{bmatrix}^{T}$ 为关于参考坐标系 $O-xyz$ 的旋转轴的单位向量。为了导出表示绕轴 $r$ 旋转角度 $\theta$ 的旋转矩阵 $R\left ( \theta ,r \right )$ ，方便的做法是对绕参考坐标系的坐标轴的基本旋转进行合成。如果旋转是绕轴 $r$ 逆时针方向进行的，则角度为正。

如图3.10所示，一个可能的解决方案是首先将轴 $r$ 旋转必要的角度，使之与 $z$ 轴一致，然后绕 $z$ 轴旋转 $\theta$ 度，最后旋转必要的角度使单位向量与初始方向一致。具体的，旋转序列如下所示，其中旋转始终是相对固定坐标系的轴进行的：

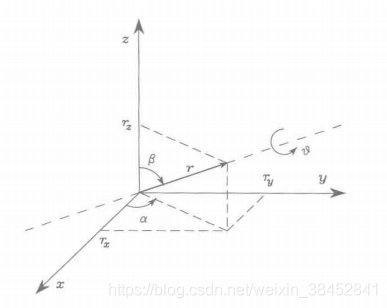
图3.10 绕一轴旋转一定的角度

使得 $r$ 与 $z$ 一致，方法是先绕 $z$ 转 $-\alpha$ 角，再绕 $y$ 转 $-\beta$ 角。
绕 $z$ 转 $\theta$ 角。
重排使与 $r$ 的初始指向一致，方法是先绕 $y$ 转 $\beta$ 角，再绕 $z$ 转 $\alpha$ 角。

归纳起来，最终的旋转矩阵为

$R\left ( \theta ,r \right )=R_{z}\left ( \alpha \right )R_{y}\left ( \beta \right )R_{z}\left ( \theta \right )R_{y}\left ( -\beta \right )R_{z}\left ( -\alpha \right )$ （3.24）

通过单位向量的分量，可以提取出需要用于计算式（3.24）中旋转矩阵的超越函数，以便消除对和的依赖。实际上，有

$sin\alpha =\frac{r_{y}}{\sqrt{r_{x}^{2}+r_{y}^{2}}}$ $cos\alpha =\frac{r_{x}}{\sqrt{r_{x}^{2}+r_{y}^{2}}}$

$sin\beta =\sqrt{r_{x}^{2}+r_{y}^{2}}$ $cos\beta =r_{z}$

于是可以发现相应于给定角度和轴的旋转矩阵为

$R\left ( \theta ,r \right )=\begin{bmatrix} r_{x}^{2}\left ( 1-c_{\theta } \right )+c_{\theta} & r_{x}r_{y}\left ( 1-c_{\theta } \right )-r_{z}s_{\theta} &r_{x}r_{z}\left ( 1-c_{\theta } \right )+r_{y}s_{\theta } \\ r_{x}r_{y}\left ( 1-c_{\theta } \right )+r_{z}s_{\theta } & r_{y}^{2}\left ( 1-c_{\theta } \right )+c_{\theta}& r_{y} r_{z}\left ( 1-c_{\theta } \right )-r_{x}s_{\theta }\\ r_{x}r_{z}\left ( 1-c_{\theta } \right )-r_{y}s_{\theta } & r_{y}r_{z}\left ( 1-c_{\theta } \right )+r_{x}s_{\theta }&r_{z}^{2}\left ( 1-c_{\theta } \right )+c_{\theta} \end{bmatrix}$ （3.25）

该矩阵具有如下的性质：

$R\left ( -\theta ,-r \right )=R\left ( \theta ,r \right )$ （3.26）

即，绕 $-r$ 旋转 $-\theta$ 与绕 $r$ 旋转 $\theta$ 没有区别，因此，这种表示不是唯一的。

如果需要求问题的逆解以计算相应于如下给定旋转矩阵的轴和角度

$R=\begin{bmatrix} r_{11} & r_{12}&r_{13} \\ r_{21}& r_{22} & r_{23}\\ r_{31}& r_{32} & r_{33 \end{bmatrix}$

以下结论是有用的：

$\theta =arccos\left ( \frac{r_{11}+r_{22}+r_{33}-1}{2} \right )$ （3.27）

$r=\frac{1}{2sin\theta }\begin{bmatrix} r_{32}-r_{23}\\ r_{13}-r_{31}\\ r_{21}-r_{12} \end{bmatrix}$ （3.28）

其中 $sin\theta \neq 0$ ，注意表达式（3.27）、（3.28）是通过4个变量来描述旋转的，即角度量和轴的单位向量的3个分量。但是，易知 $r$ 的3个分量不是独立的，而是受到以下条件的约束

$r_{x}^{2}+r_{y}^{2}+r_{z}^{2}=1$ （3.29）

如果 $sin\theta= 0$ ，表达式（3.27）和（3.28）将失去意义。为了求解逆问题，有必要直接参考通过旋转矩阵 $R$ 得到的特定表达式，并找到 $\theta =0$ 和 $\theta =\pi$ 情形下的求解公式。注意到，当 $\theta =0$ （不旋转）时，单位向量是任意的。

3.6 单位四元数

角度/轴表达式的不足可以通过一个不同的四参数表达式加以克服。即单位四元数（unit quaternion），也就是欧拉参数，定义为 $Q=\left \{ \eta ,\epsilon \right \}$ ，其中：

$\eta =cos\frac{\theta }{2}$ （3.30）

$\epsilon =sin\frac{\theta }{2}r$ （3.31）

$\eta$ 称为四元数的标量部分，而 $\epsilon = \begin{bmatrix} \epsilon_{x} & \epsilon_{y} & \epsilon_{z} \end{bmatrix}^{T}$ 称为四元数的向量部分。它们受到以下条件的约束

$\eta ^{2}+\epsilon _{x}^{2}+\epsilon _{y}^{2}+\epsilon _{z}^{2}=1$ （3.32）

从而将其称为单位四元数。考虑到式，相应于给定四元数的旋转矩阵有以下形式，

$R\left ( \eta ,\varepsilon \right )=\begin{bmatrix} 2\left ( \eta ^{2}+\epsilon _{x}^{2} \right )-1 & 2\left ( \epsilon _{x}\epsilon _{y}-\eta \epsilon _{z} \right ) &2\left ( \epsilon _{x}\epsilon _{z}+\eta \epsilon _{y} \right ) \\ 2\left ( \epsilon _{x}\epsilon _{y}+\eta \epsilon _{z} \right ) &2\left ( \eta ^{2}+\epsilon_{y}^{2}\right ) -1 &2\left ( \epsilon _{y}\epsilon _{z}-\eta \epsilon _{x} \right ) \\ 2\left ( \epsilon _{x}\epsilon _{z}-\eta \epsilon _{y} \right ) &2\left ( \epsilon _{y}\epsilon _{x} \right ) & 2\left ( \eta ^{2}+\epsilon_{z}^{2}\right )-1 \end{bmatrix}$ （3.33）

如果要求解逆问题，以计算相应于如下给定旋转矩阵的四元数

$R=\begin{bmatrix} r_{11} & r_{12}&r_{13} \\ r_{21}& r_{22} & r_{23}\\ r_{31}& r_{32} & r_{33 \end{bmatrix}$

以下结论是有用的：

$\eta =\frac{1}{2}\sqrt{r_{11}+r_{22}+r_{33}+1}$ （3.34）

$\epsilon =\frac{1}{2}\begin{bmatrix} sgn(r_{32}-r_{23})\sqrt{r_{11}-r_{22}-r_{33}+1}\\ sgn(r_{13}-r_{31})\sqrt{r_{22}-r_{33}-r_{11}+1}\\ sgn(r_{21}-r_{12})\sqrt{r_{33}-r_{11}-r_{22}+1} \end{bmatrix}$ （3.35）

其中，按照惯例，当 $x\geqslant 0$ 时， $sgn(x)=1$ ，当 $x< 0$ 时， $sgn(x)=-1$ 。注意到在式（3.34）中已经隐含了假定 $\eta\geqslant 0$ ，这相当于角度 $\theta\in \begin{bmatrix} -\pi & \pi \end{bmatrix}$ ，这样就可以描述所有的旋转。同时，与式（3.27）和式（3.28）中关于角度和轴的表达式的逆解相比，没有式（3.34）和（3.35）中的奇点现象。

从 $R^{-1}=R^{T}$ 提取的四元数记为 $Q^{-1}$ ，可以如下进行计算

$Q^{-1}=\left \{ \eta ,-\epsilon \right \}$

令 $Q_{1}=\left \{ \eta _{1},\epsilon _{1} \right \}$ 和 $Q_{2}=\left \{ \eta _{2},\epsilon _{2} \right \}$ 分别表示相应于旋转矩阵的 $R_{1}$ 和 $R_{2 }$ 的四元数。相应于乘积 $R_{1}R_{2}$ 的四元数为

$Q_{1}\ast Q_{2}=\left \{ \eta _{1}\eta _{2}-\epsilon _{1}^{T}\epsilon _{2},\eta _{1}\epsilon _{2} +\eta _{2}\epsilon _{1}+\epsilon _{1}\times \epsilon _{2}\right \}$