如果需要小编其他数学基础博客,请移步小编的GitHub地址
传送门:请点击我
如果点击有误:https://github.com/LeBron-Jian/DeepLearningNote
这里我打算补充一下机器学习涉及到的一些关于特征值和特征向量的知识点。
(注意:目前自己补充到的所有知识点,均按照自己网课视频中老师课程知识点走的,同时一些公式是网友辛辛苦苦敲的,这里用到那个博客均在文末补充地址,不过这里首先表示感谢!!)
这里学习特征值和特征向量之前先说一下机器学习中特征提取的特征向量与矩阵的特征向量的区别
我的理解是机器学习的特征向量是指你所提取的特征组成的向量(也称为 feature vector),这个特征可以是任意的,比如人的身高体重,头发的长短等,单位也是由自己决定,完全看你的需求。而矩阵的特征向量(称为 eigen vector)是线性代数里的概念,是对矩阵求解特征方程得到的向量。不过这里我主要学习线性代数中矩阵的特征值和特征向量。
1,预备知识
1.1 标量
一个标量就是一个单独的数,一般用小写的变量名称表示。
1.2 向量
一个向量就是一列数,这些数是有序排列的。用过次序中的索引,我们可以确定每个单独的数。通常会赋予向量粗体的小写名称。当我们需要明确表示向量中的元素时,我们会将元素排列成一个方括号包围的纵柱:
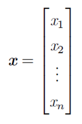
我们可以把向量看做空间中的点,每个元素是不同的坐标轴上的坐标。
1.3 矩阵
矩阵是二维数组,其中的每一个元素被两个索引而非一个所确定。我们通常会赋予矩阵粗体的大写变量名称,比如A。如果一个实数矩阵高度为 m,宽度为 n,那么我们说 A属于Rm*n。
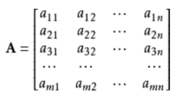
矩阵在机器学习中非常重要,实际上,如果我们现在有N个用户的数据,每条数据含有M个特征,那其实它对应的就是一个N*M的矩阵;再比如,一张图由 16*16的像素点组成,那就是一个16*16的矩阵。
1.4 张量
几何代数中定义的张量是基于向量和矩阵的推广,通俗一点理解的话,我们可以将标量视为零阶张量,矢量视为一阶张量,那么矩阵就是二阶张量。
例如,可以将任意一张彩色图片表示成一个三阶张量,三个维度分别是图片的高度,宽度和色彩数据。将这张图用张量表示出来,就是最下面的这张表格:
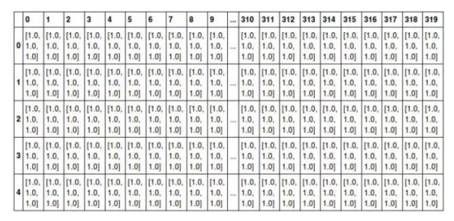
其中表的横轴表示图片的宽度值,这里只截取0~319;表的纵轴表示图片的高度值,这里只截取0~4;表格中每个方格代表一个像素点,比如第一行和第一列的表格数据为 [1.0, 1.0, 1.0],代表的就是 RGB三原色在图片的这个位置的取值情况(即R=1.0, G=1.0, B=1.0)。
当然我们还可以将这一定义继续扩展,即:我们可以用四阶张量表示一个包含多张图片的数据集,这四个维度分别是:图片在数据集中的编号,图片高度,宽度以及色彩。
张量在深度学习中是一个很重要的概念,因为它是一个深度学习框架中的核心组件,后续的所有运算和优化算法是基于张量进行的。
1.5 范数
有时我们需要衡量一个向量的大小。在机器学习中,我们经常使用被称为范数(norm)的函数衡量矩阵大小,Lp范围如下:
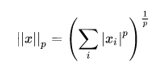
所以:L1 范数 ||x||:为 x 向量各个元素绝对值之和;L2 范数 ||x||2 为 x 向量各个元素平方和的开方。
1.6 方差
方差用来度量随机变量 X 与其数学期望 E(X) 的偏离程度,公式为:
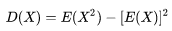
方差总数一个非负数,当随机变量的可能值集中在数学期望的附加时,方差较小;反之方差大。由方差的大小可以推断出随机变量分布的分散程度。
1.7 协方差
协方差用来刻画两个随机变量 X, Y 的相关性,公式为:
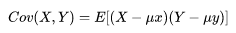
如果协方差为正,说明X, Y 同向变化,协方差越大说明同向程度越高
如果协方差为负,说明X, Y反向运动,协方差越小说明反向程度越高
对于上述“同向”和“反向”的理解:
- 1,你变大,同时我也变大,说明两个变量是同向变化的,这时协方差就是正的
- 2,你变大,同时我变小,说明两个变量是反向变化的,这时协方差就是负的
- 3,从数值来看,协方差的数值越大,两个变量同向程度也就越大。反之亦然
1.8 相关系数
用随机变量X,Y的协方差除以X的标准差和Y的标准差,公式为:
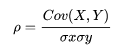
相关系数也可以看成是协方差:一种剔除了两个变量量纲,标准化后的协方差。
相关系数是一种标准化后的协方差,有以下特点:
- 1)也可以反映两个变量变化时是同向还是反向,如果同向变化就为正,反向变化就为负
- 2)它消除了两个变量变化幅度的影响,而只是单纯反应两个变量每单位变化时的相似程度
对于两个随机变量:
- 1,当他们的相关系数为1时,说明两个变量变化时的正向相似度最大,即你变大一倍,我也变大一倍;你变小一倍,我也变小一倍。也就是完全正相关(以X, Y为横纵坐标轴,可以画出一条斜率为正数的直线,所以X,Y是线性关系的)
- 2,随着他们相关系数减小,两个变量变化时的相似度也变小,当相关系数为0时,两个变量的变化过程没有任何相似度,也即两个变量无关
- 3,当相关系数继续变小,小于0时,两个变量开始出现反向的相似度,随着相关关系继续变小,反向相似度会逐渐变大。
- 4,当相关系数为 -1 时,说明两个变量变化的反向相似度最大,即,你变大一倍,我变小一倍;你变小一倍,我变大一倍。也即是完全负相关(以X, Y为横纵坐标轴,可以画出一条斜率为负数的直线,所以X, Y也是线性关系的)
1.9 协方差矩阵
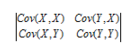
协方差只能处理二维问题,即两个随机变量的相关程度
维度多了就需要计算多个协方差,于是出现了协方差矩阵
协方差矩阵的每一个值就是对应下标的两个随机变量的协方差(即相关程度)
可以看出,协方差矩阵是一个对称矩阵,而且对角线是各个维度的方差。
Python代码举例:
import numpy as np X = np.array([[-2.1,-1,4.3],[3,1.1,0.12],[3,1.1,0.12]]) #每一行代表一个随机变量,每列代表随机变量的值 #[[-2.1,-1,4.3], # [3,1.1,0.12], # [3,1.1,0.12]] print(np.cov(X)) #[[ 11.71 , -4.286 , -4.286 ], # [ -4.286 , 2.14413333, 2.14413333], # [ -4.286 , 2.14413333, 2.14413333]])
2,特征的特征值和特征向量的抽象理解
特征值(eigenvalue)和特征向量(eigenvector)具有共同前缀 eigen-,其起源于德语,意为“特征”,而Eigen的英文本意为“本证的,固有的,特有的”意思。再看一下计算特征值所需要的特征行列式所对应的英文单词是 determinant,意思是“决定性的,名词决定性因素”。
首先我们应该充分理解“特征”的含义:对于线性代数而言,特征向量和特征值体现了矩阵的本质,“特征”强调了单个矩阵的特点,相当于它的 ID card。
从线性代数的角度出发,如果把矩阵看做 n 维空间下的一个线性变换,这个变换有很多的变换方向,我们通过特征值分解得到的前N个特征向量,那么就对应了这个矩阵最主要的N个变化方向。我们利用这前N个变化方向,就可以近似这个矩阵(变换)。其中的N个变化方向,就是这个矩阵最重要的“特征”。
有了特征的概念之后,我们又如何理解特征值与特征向量呢?可以做这样的比喻:
- 1,如果把矩阵看做是位移,那么特征值 = 位移的速度,特征向量 = 位移的方向
- 2,特征向量在一个矩阵的作用下作伸缩运动,伸缩的幅度由特征值确定(注意观察定义式)。特征值大于1,所有属于此特征值的特征向量变长;特征值属于(0, 1),特征向量缩短;特征值小于0,特征向量则反向延长。

3,特征值的数学定义
3.1 特征值和特征向量的定义
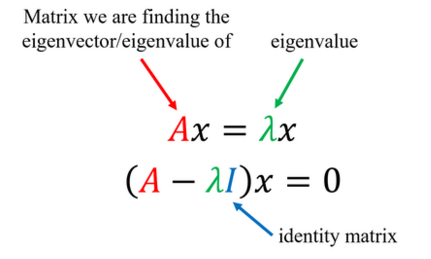
数学定义:对于给定矩阵A,寻找一个常数 λ 和非零向量 x,使得向量 x被矩阵 A 作用后所得的向量 Ax 与原向量 x 平行,并且满足 Ax = λx,则称 λ 为矩阵 A 的一个特征值(标量),X为矩阵 A 对应于特征值的一个特征向量(1*n)。
该式子可理解为向量 x 在几何空间中经过矩阵 A的变换后得到向量 λx。由此可知,向量 X 经过矩阵 A 变化后,只是大小伸缩了 λ 倍。总而言之:特征向量提供了复杂的矩阵乘法到简单的数乘之间的转换。
从解题角度,我们再看如何求特征值和特征向量:设向量 x 为矩阵 A对应于特征值 λ 的特征向量,即 Ax = λx,则有 (A – λI)x = 0,所以求解 x 就是求解 (A – λI)x = 0 中 x 的非零解。其中 I 为单位矩阵,因此 | λI -A) 称为 X 的特征多项式。
3.2 特征值和特征向量的推论
我们有以下推论:
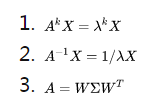
其中第三个是特征值分解公式,W为 n*n 的特征向量矩阵(n个大小为 1*n 的特征向量 X组成)。Σ 是包含对应特征值的对角矩阵。根据不同的特征值的大小,可知道每个特征向量对应权重,即其重要性。
3.3 特征子空间
特征子空间(characteristic subspace)是一类重要的子空间,即对应于线性变换的一特征值的子空间。设V是域P上的线性空间,σ 的对应于特征值 λ0 的全体特征向量与零向量所组成的集合。特征空间中包含了所有的特征向量
我们知道,对于n阶方阵,可得:
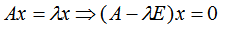
而 x != 0,即齐次线性方程组(*λ)有非零解
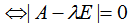
方程组(*λ)的解空间称为对应于 λ 的特征子空间。
3.4 特征多项式
设:
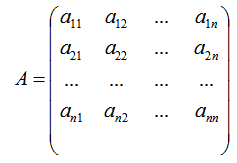
则称:
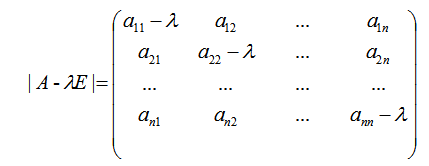
为矩阵 A 的特征多项式,记为 f(λ)。
4,特征值和特征向量的意义
4.1 特征值和特征向量的代数意义
矩阵乘法从表面来讲,是前一个矩阵的行乘以后一个矩阵的列(前提是前一个矩阵的行数等于后一个矩阵的列数);它的真正含义是变换,我们学习高等代数一开始就学习行变换列变换,所以矩阵乘法就是线性变换。
再来说一下其定义,如果存在向量 Vi,常数 λi,使得以下式子成立,则称常数 λi 为方阵A的特征值,而向量 Vi 则是可对角化方阵 A的特征向量:
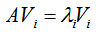
特征向量的代数上含义是:将矩阵乘法转换为数乘操作;
4.2 特征值分解的几何意义
特征向量的几何上含义是:特征向量通过方阵 A 变换变换只进行缩放,而特征向量的方向仍然不变。
特征值分解可以写成以下形式:
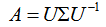
其中 U 是由 A 的特征向量组成的矩阵,也是方阵,Σ 是对角矩阵,对角线上是对应的特征值,可以对特征向量 ui 进行正交单位化,这样矩阵A就可以表示为以下形式:
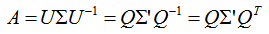
其中 Q 为 U 进行单位正交化后的矩阵, Σ ‘ 还是对角矩阵,对角线上是对应的特征值,因为 Q 中的列向量都是单位正交的,所以 QTQ = E ,从而 Q-1 = QT。
比如下面一个矩阵:
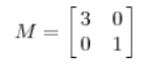 它其实对应的线性变换是下面的形式:
它其实对应的线性变换是下面的形式:
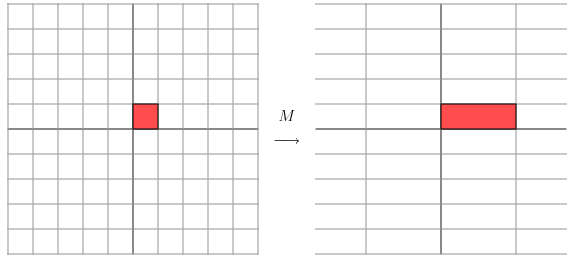
因为这个矩阵M乘以一个向量(x, y)的结果是:
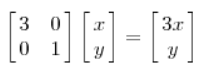
上面的矩阵是对称的,所以这个变换时一个对 x, y 轴的方法一个拉伸变换(每一个对角线上的元素将会对一个维度进行拉伸变换,当值 > 1,是拉伸,当值 < 1 的时候是缩短)。
下面再看另一个对称矩阵:
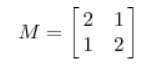
此对称矩阵,它对坐标轴(正交)的影响如下:
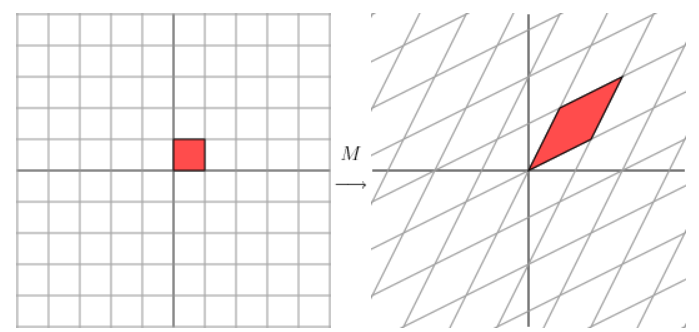
将上面右边的坐标轴(图中黑色十字)逆时针旋转 45 度,将会看到:
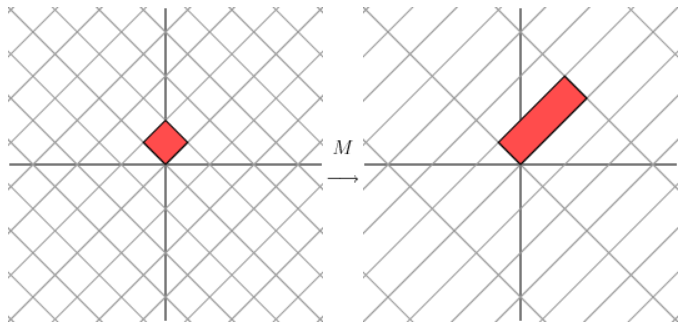
这样就和最开始的对角矩阵的变换类似了,在某个坐标轴的方向上伸长了3倍,这次的坐标轴发生了旋转,用数学语言就是,给定一个对称矩阵M,存在一个向量V,将M右乘向量V,将M右乘向量V,相当于将这个向量缩放了 λ 倍。式子表达如下:
MVi = λiVi
其中Vi 称为矩阵M的特征向量,λi 称为矩阵M的特征值。所以我们可以得到以下结论:
- (1) 当一个向量左乘一个对角阵时,相当于对这个向量的长度进行缩放,此处坐标轴并没有发生变化。
- (2) 当一个向量左乘一个对称阵时,相当于对这个向量的长度进行缩放,而且对坐标轴进行了选择。
下面看一个更一般的矩阵,我们是否能将其从一组标准正交基变换到另一组正交基,当矩阵不是对称的时候,比如说矩阵是下面的样子:
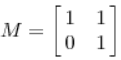
它所描述的变化是下面的样子:
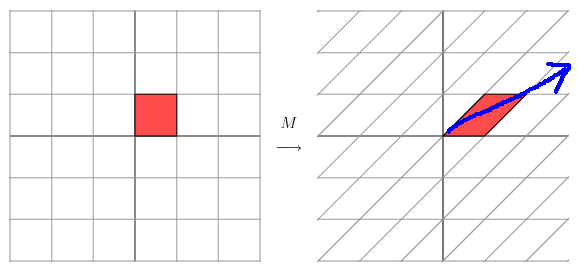
这其实是在平面上对一个轴进行的拉伸变换(如蓝色的箭头所示),在图中,蓝色的箭头是一个最主要的变化方向(变化的方向可能不止一个)。
此时的两条坐标轴并不是正交的,如果将右图中的坐标轴旋转 30度,我们将会看到:
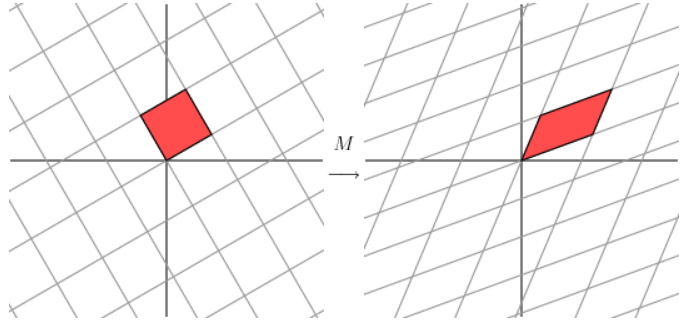
然后再对坐标轴旋转60度,将会看到
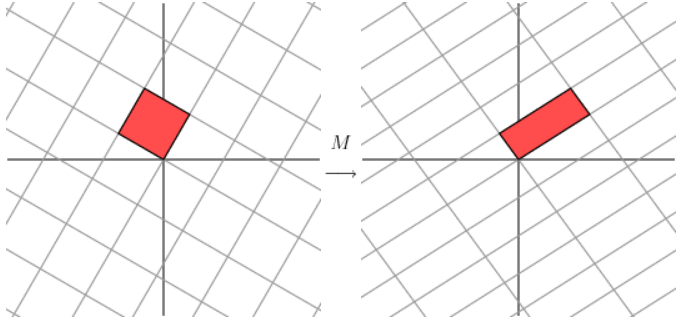
此时,两条坐标轴已经是正交的,说明对于任意的矩阵,我们都能找到一组坐标轴,它由原来的坐标轴通过旋转和缩放得到。用几何意义表达如下:
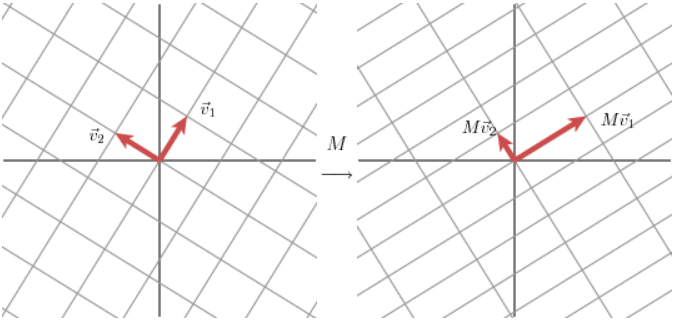
如上图所示,对于二维矩阵M,我们总能找到一组标准正交基V1和V2,使得 MV1 和 MV2 是正交的,我们用另一组标准正交基U1和U2表示 MV1 和 MV2 的方向,这样就将M从一组标准正交基用另一组标准正交基来表示。
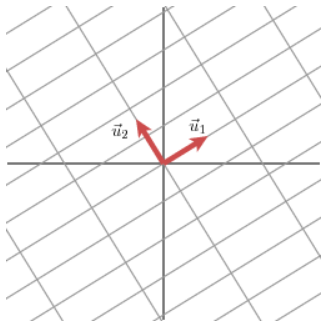
注意:标准正交基
在线性代数中,一个内积空间的正交基(orthogonal basis)是元素两两正交的基,称基中的元素为基向量。假若一个正交基的基向量的模长都是单位长度 1,则称这正交基为标准正交基或规范正交基。
5,特征向量的应用
既然特征值表达了重要程度且和特征向量所对应,那么特征值大的就是主要信息了,基于这点我们可以提取各种有价值的信息了!我们都知道线性代数中,左乘一个矩阵是对应着行变换,右乘一个矩阵对应列变换,其实际的作用也就是对常规坐标系进行了迁移。那么对于在普通二维坐标下的向量 x ,它在矩阵 A 描述空间中的表示与自己单纯的进行拉伸或缩放的效果是一致的,满足这种特殊性的 X 就是特征矩阵,对应的拉伸量 λ 就是特征值。
有了这个特殊的性质,特征值与特征向量出现在很多有矩阵运算的地方,如主成分分析(PCA),奇异值分解(SVD) 等机器学习方法中。
图像处理中的 PCA 降维方法(最著名的),选取特征值最高的 k个特征向量来表示一个矩阵,从而达到降维分析 + 特征显示的方法,还有图像压缩的 K-L 变换。再比如很多人脸识别,数据流模式挖掘分析等方面。

如上图所示,原图如左图所示,提取最重要的n个特征来表示,我们发现仍然可以显示这个图的主要特征。
6,矩阵特征值的一般求解
6.1 特征值的求解步骤
特征值的求解过程如下:
- 1,计算特征多项式 |A – λE|
- 2,求 |A – λE| = 0 的所有根,即 A 的所有特征值
- 3,对于每个特征值 λ0,求解齐次线性方程组 (A – λ0E)x = 0 的一个基础解系 ξ1….ξt,则 x=k1ξ1 + …..+ ktξt 为 A 对应于 λ0 的全部特征向量(k1, …kt 不全为0)
6.2 求矩阵 A 的特征值和特征向量
矩阵A如下:
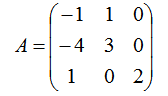
我们首先求其特征多项式,通过其特征方程,求解特征值。
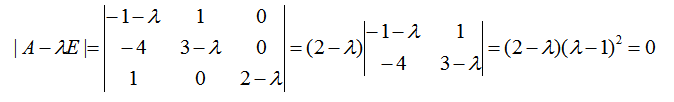
则特征值为 λ =2, 1。
然后把每个特征值 λ 代入线性方程组 (A – λE)x = 0中,求出基础解系。
当 λ = 2 时,解线性方程组 (A – 2E)x = 0,如下:
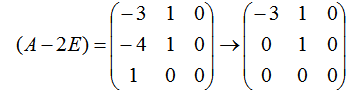

当 λ = 1 时,解线性方程组 (A – E)x = 0,如下:
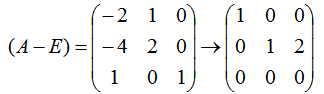

7,通过特征值和特征向量进行PCA降维
7.1 PCA降维的算法步骤
设有 m 条 n 维数据:
- 1,将原始数据按照列组成 n 行 m 列矩阵 X
- 2,将 X 的每一行进行零均值化(去平均值),即减去这一行的均值
- 3,求出协方差矩阵 C = 1/m*X*XT
- 4,求出协方差矩阵的特征值以及对应的特征向量
- 5,将特征向量按对应特征值大小从上到下按行排列成矩阵,取前 k 行组成的矩阵P(保留最大的 k 的各特征向量)
- 6,Y = PX 即为降维到K维后的数据
7.2 PCA 降维的计算实例
1,原始数据集矩阵X:

2,均值为(2, 3),求均值后:

3,再求协方差矩阵(C= 1/m*X*XT):
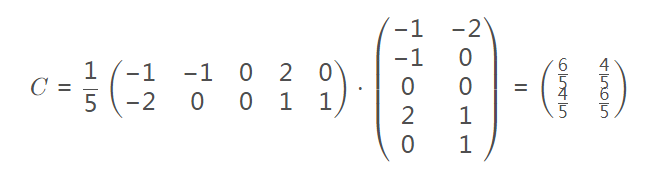
4,特征值:
通过协方差矩阵C的特征方程,求出特征值:

得到:
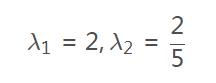
5,求出对应的一组特征向量:
把每个特征值代入线性方程组(A – λE)x =0,求出其基础解系,并得到一组特征向量。
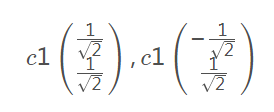
6,标准化:
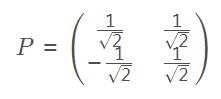
7,选择较大特征值对应的特征向量:
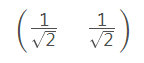
8,执行PCA变换:Y=PX 得到的Y就是PCA降维后的值 数据集矩阵:

8,通过特征值和特征向量进行SVD 计算
8.1 SVD分解步骤
首先,我们展示一下SVD分解的公式:
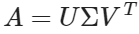
进行SVD分解的步骤就是:
1,求U(U中的每个特征向量叫做A的左奇异向量)
从下面公式我们可以发现,AAT的特征向量组成的就是U向量:
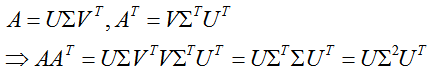
2,求V(V中的每个特征向量叫做A的右奇异向量)
从下面公式我们可以发现:ATA 的特征向量组成的就是V矩阵:
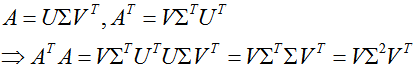
3,求Σ
所以先求出ATA和 AAT,进而求出ATA和 AAT 的特征值和特征向量,然后得到U和V,最后通过 σi = √λi 直接求出奇异值,然后代入我们上面的奇异值分解公式,得到奇异值分解。
8.2 SVD计算实例
我们需要进行奇异值分解的矩阵A如下:
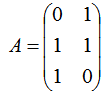
我们首先求出 ATA和 AAT:

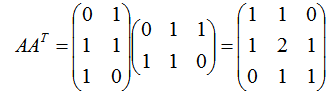
进行求出 ATA 的特征值和特征向量:
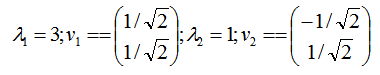
接着求 AAT 的特征值和特征向量:
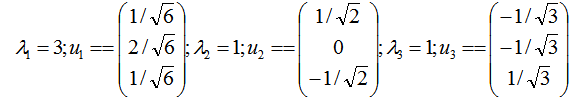
利用 Avi=σiui,i=1,2 求奇异值:
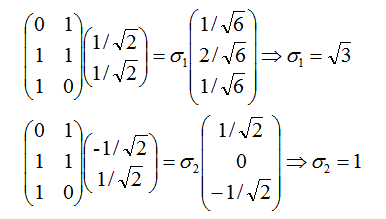
当然,我们也可以用 σi = √λi 直接求出奇异值为 √3 和 1。
最终得到 A 的奇异值分解为:
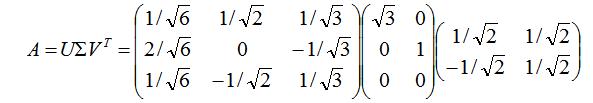
参考地址:
https://zhuanlan.zhihu.com/p/165382601
https://zhuanlan.zhihu.com/p/36584206
https://zhuanlan.zhihu.com/p/126102942
https://www.zhihu.com/question/29589753/answer/1635329454
https://www.zhihu.com/search?type=content&q=%E6%9C%BA%E5%99%A8%E5%AD%A6%E4%B9%A0%E7%89%B9%E5%BE%81%E5%80%BC%E5%92%8C%E7%89%B9%E5%BE%81%E5%90%91%E9%87%8F%E7%9A%84%E7%9F%A5%E8%AF%86%E7%82%B9%E3%80%82





