抽空看了一段时间的粒子群算法,这里仅针对其应用于动态规划中的背包问题的情况做下总结归纳,其他应用可以之后想到了再添加。
如果这篇文章看完了的话,可以举一反三,将下面的代码稍微改动一下做一个二维函数的求最小值问题,点击链接可以直达哦。
一:分组背包问题简介
假设有3个组,每组有2个物品,每种物品有3种属性,价值、体积和重量。我们只有1个背包,从每组中选择1个物品(可以不选的情况第三章讨论)装入背包中,如何选择才能使背包中的物品总价值最大、总体积最小、且不超过规定重量呢?
| 物品/分组 | 第一组 | 第二组 | 第三组 |
|---|---|---|---|
| 物品1价值 | 1 | 2 | 3 |
| 物品2价值 | 3 | 2 | 1 |
| 物品/分组 | 第一组 | 第二组 | 第三组 |
|---|---|---|---|
| 物品1体积 | 1 | 2 | 1 |
| 物品2体积 | 2 | 1 | 2 |
| 物品/分组 | 第一组 | 第二组 | 第三组 |
|---|---|---|---|
| 物品1质量 | 20 | 50 | 40 |
| 物品2质量 | 30 | 40 | 20 |
由于上诉情况数较少,我们穷举就能列完:
| 每组选第几物品 | 背包总价值 | 背包总体积 | 背包总重量 |
|---|---|---|---|
| 1 1 1 | 6 | 4 | 110 |
| 1 1 2 | 4 | 5 | 90 |
| 1 2 1 | 6 | 3 | 100 |
| 1 2 2 | 4 | 4 | 80 |
| 2 1 1 | 8 | 5 | 120 |
| 2 1 2 | 6 | 6 | 100 |
| 2 2 1 | 8 | 4 | 110 |
| 2 2 2 | 6 | 5 | 90 |
假设背包总重量的限制为110的话,从穷举中我们可以知道此时第一组物品2、第二组物品2、第三组物品1这样选有总价值8、总体积4这样的最优解。下面将介绍如何用粒子群算法求解此类问题。
二:粒子群算法解分组背包问题
一般说到背包问题都会想到用动态规划DP的方法去解决,DP确实很精炼简洁,但是状态转移方程的理解不易。粒子群算法过程长了些,但其思想很朴素,更自然。
先说说学习理解了算法过后,对这算法运算过程的感性描述:
- 随机产生了一堆粒子,每个粒子代表背包的一种情况(选了哪3个物品),初始粒子全都是局部最优粒子。
- 计算每个粒子的适应度值(也就是每个粒子代表的背包的价值、体积、重量),然后每个粒子适应度按优劣选出初始非劣粒子。
- 之后进入迭代过程,每次迭代中,从非劣粒子中随机选一个作为全局最优粒子,按照公式计算粒子速度(跟较优粒子和全局最优粒子息息相关),使每个粒子产生移动(也就是有概率替换代表的物品)。
- 如果移动后的粒子比之前的粒子更优则替代原来的局部最优粒子
- 然后把非劣粒子和局部最优粒子放一起,再按优劣选出非劣粒子
- 去除重复的非劣粒子,进入下一次迭代。
注意加粗的部分都是算法的关键步骤!
自己设置迭代次数,粒子群算法收敛很快,最后如果有最优解的话,我们会得到一堆非劣解粒子,选择里面价值最大且体积小的情况就可以啦!
重点是看程序是如何实现的,下面将完整的MATLAB代码分解成2.1~2.7七部分讲解。
2.1 输入参数、固定参数初始化
clear, clc, close all;
%% 输入参数、固定参数初始化
P = [1 2 3; 3 2 1]; % 各组物品价值
V = [1 2 1; 2 1 2]; % 各组物品体积
M = [20 50 40; 30 40 20]; % 各组物品重量
group = size(P, 2); % 组数
nitem = size(P, 1); % 每组物品数
weight = 120; % 背包最大重量限制
xsize = 50; % 粒子数
ITER = 200; % 迭代次数
c1 = 0.8; c2 = 0.8; % 常数
wmax = 1.2; wmin = 0.1; % 惯性权重相关常数
v = zeros(xsize, group); % 粒子速度初始化
2.2 粒子群位置、适应度、最佳位置、最佳适应度初始化
随机产生粒子群\(x\),表示每组选哪个物品(其实就是产生了一群背包),比如\(x_i = [1, 2, 1]\)的时候,表示第\(i\)个粒子取第一组第1个物品、第二组第1个物品、第三组第1个物品
注意粒子与粒子群位置是一个意思。有时候可能会混用。
适应度其实就是用粒子群位置算出其代表的背包的价值、体积、质量。
%% 粒子群位置、适应度、最佳位置、最佳适应度初始化
x = randi(nitem, xsize, group); % 随机粒子群位置(表示每组选哪个物品)
% 粒子群适应度
xp = zeros(1, xsize); % 粒子群价值
xv = zeros(1, xsize); % 粒子群体积
xm = zeros(1, xsize); % 粒子群重量
for i = 1 : xsize
for j = 1 : group
xp(i) = xp(i) + P(x(i, j), j);
xv(i) = xv(i) + V(x(i, j), j);
xm(i) = xm(i) + M(x(i, j), j);
end
end
bestx = x; % 粒子群位置最佳值
bestp = xp; bestv = xv; bestm = xm; % 粒子群最佳适应度
2.3 初始筛选非劣解
第一次筛选非劣解,之后每次迭代都会重新筛选一次。其中的判断条件很重要,可以根据问题的限制而改变。这里就是判断每个粒子是否比别的所有粒子都更符合要求(价值大且体积小)。
如果还限制了背包体积大小的话,还需要在判断中加上对粒子体积的限制。这里只限制了背包重量。
%% 初始筛选非劣解
cnt = 1;
for i = 1 : xsize
fljflag = 1;
for j = 1 : xsize
if j ~= i
if (xp(j) > xp(i) && xv(j) < xv(i)) ||... % i粒子劣解
(xp(j) > xp(i) && xv(j) == xv(i)) ||...
(xp(j) == xp(i) && xv(j) < xv(i)) || (xm(i) > weight)
fljflag = 0;
break;
end
end
end
if fljflag == 1
flj(cnt, :) = [xp(i), xv(i), xm(i)]; % 非劣解适应度
fljx(cnt, :) = x(i, :); % 非劣解位置
cnt = cnt + 1;
end
end
for niter = 1 : ITER % 迭代开始,粒子开始运动
rnd = randi(size(flj, 1), 1, 1);
gbest = fljx(rnd, :); % 粒子全局最优解
2.4 粒子运动计算
粒子速度的计算算是粒子群算法的精华了,其中有根据惯性权值计算粒子速度的公式:
\[v^{i+1} = wv^i + c1r1(p_{local}^i – x^i) + c2r2(p_{global} – x^i) \]
其中\(w\)为惯性权值,\(c1\)和\(c2\)为常数,\(r1\)和\(r2\)为[0,1]间服从均匀分布的随机数,\(p_{local}^i\)是局部最优粒子,\(p_{global}\)是全局最优粒子,注意只有一个所以没有上标\(i\)。
惯性权值的取值跟迭代次数有关,这里我们采用\(w = wmax-(wmax – wmin) * niter / iterall\)这样的计算方法。相关惯性权值的计算也是粒子群算法研究的热点,惯性权值变化大,粒子速度快,位置变换也快,惯性权值取得好的话可以使粒子群更快的收敛到全局最优!
在用速度对每个粒子位置进行更新时,注意两个问题,一是粒子位置可能取到大于物品总数的值了,所以这里我们取了一个模值;二是粒子运动后可能会产生负的值,总不能取到第-2个物品吧,所以在这里的处理方法是对负数取一个小于等于物品数的随机正整数。最后记得对运动后的粒子位置值四舍五入(当然也可以别的方法比如向上取整,只要保证位置不超过每组物品的数量就可以咯)。
%% 粒子运动计算
w = wmax - (wmax - wmin) * niter / ITER; % 惯性权值更新
r1 = rand(1,1); r2 = rand(1,1); % 产生[0, 1]间均匀分布随机值
for i = 1 : xsize
v(i, :) = w * v(i, :) + c1 * r1 * (bestx(i, :) - x(i, :)) + c2 * r2 * (gbest - x(i, :)); % 粒子速度
x(i, :) = x(i, :) + v(i, :);
x(i, :) = rem(x(i, :), nitem); % 不能超过物品数
index = find(x(i, :) < 0.5); % 运动后小于0.5了,用新的随机整数代替
if ~isempty(index)
x(i, index) = randi(nitem, 1, length(index));
end
x(i, :) = round(x(i, :)); % 四舍五入取整
end
2.5 当前粒子群适应度、最佳位置、最佳适应度
粒子经过了运动到了新的位置,当然要把新粒子和旧粒子拿出来比一比,如果新粒子的适应度比旧粒子好的话,就更新局部最佳粒子位置咯。这里需要考虑一个问题,新粒子好的话更新,不好的话不更新,但是遇到新旧各有所长时怎么办呢?其实就相当于有两个背包,一个价值更高,另一个体积更小,那到底取哪一个呢?那就随机取一个吧。
%% 当前粒子群适应度、最佳位置、最佳适应度
xp_cur = zeros(1, xsize);
xv_cur = zeros(1, xsize);
xm_cur = zeros(1, xsize);
for i = 1 : xsize
for j = 1 : group
xp_cur(i) = xp_cur(i) + P(x(i, j), j);
xv_cur(i) = xv_cur(i) + V(x(i, j), j);
xm_cur(i) = xm_cur(i) + M(x(i, j), j);
end
end
for i = 1 : xsize
if (xp_cur(i) > xp(i) && xv_cur(i) < xv(i)) ||... % 如果当前粒子适应度更好
(xp_cur(i) > xp(i) && xv_cur(i) == xv(i)) ||...
(xp_cur(i) == xp(i) && xv_cur(i) < xv(i)) || (xm(i) > weight)
bestx(i, :) = x(i, :); % 粒子最佳位置更新
bestp(i) = xp_cur(i); bestv(i) = xv_cur(i); bestm(i) = xm_cur(i); % 粒子最佳适应度更新
elseif (xp_cur(i) < xp(i) && xv_cur(i) > xv(i)) ||... % 如果原始粒子适应度更好,不做处理
(xp_cur(i) < xp(i) && xv_cur(i) == xv(i)) ||...
(xp_cur(i) == xp(i) && xv_cur(i) > xv(i)) || (xm_cur(i) > weight)
continue;
else % 当前与原始粒子适应度各有所长,随机更新
if rand(1,1) < 0.5
bestx(i, :) = x(i, :); % 粒子最佳位置更新
bestp(i) = xp_cur(i); bestv(i) = xv_cur(i); bestm(i) = xm_cur(i); % 粒子最佳适应度更新
end
end
end
xp = xp_cur; xv = xv_cur; xm = xm_cur; % 新粒子变成旧粒子
2.6 粒子群最佳位置、最佳适应度合并后再筛选非劣解
与第一次做非劣解筛选的步骤基本一样,只是加了一个合并操作,把局部最佳粒子与非劣解粒子合并在一起,然后再筛选一波非劣解粒子。
%% 粒子群最佳位置、最佳适应度合并后再筛选非劣解
bestxmerge = [bestx; fljx];
pmerge = [bestp, flj(:, 1)'];
vmerge = [bestv, flj(:, 2)'];
mmerge = [bestm, flj(:, 3)'];
n = size(flj, 1);
flj = [];
fljx = [];
cnt = 1;
for i = 1 : xsize + n
fljflag = 1;
for j = 1 : xsize + n
if j ~= i
if (pmerge(j) > pmerge(i) && vmerge(j) < vmerge(i)) ||...
(pmerge(j) > pmerge(i) && vmerge(j) == vmerge(i)) ||...
(pmerge(j) == pmerge(i) && vmerge(j) < vmerge(i)) || (mmerge(i) > weight)
fljflag = 0;
break;
end
end
end
if fljflag == 1
flj(cnt, :) = [pmerge(i), vmerge(i), mmerge(i)]; % 非劣解适应度
fljx(cnt, :) = bestxmerge(i, :); % 非劣解位置
cnt = cnt + 1;
end
end
2.7 去掉重复非劣解
这一步也很重要,实现方法也有很多,随便选一种把重复的非劣解去掉就可以咯。
%% 去掉重复非劣解
issame = zeros(cnt - 1, 1);
for i = 1 : cnt - 1
for j = i + 1 : cnt - 1
if ~issame(j)
issame(j) = (length(find(fljx(j, :) == fljx(i, :))) == group);
end
end
end
flj(find(issame == 1), :) = [];
fljx(find(issame == 1), :) = [];
end
figure;
plot(flj(:, 1), flj(:, 2), 'ro');
title('粒子群结果'); xlabel('总价值'); ylabel('总体积');
2.8 结论分析
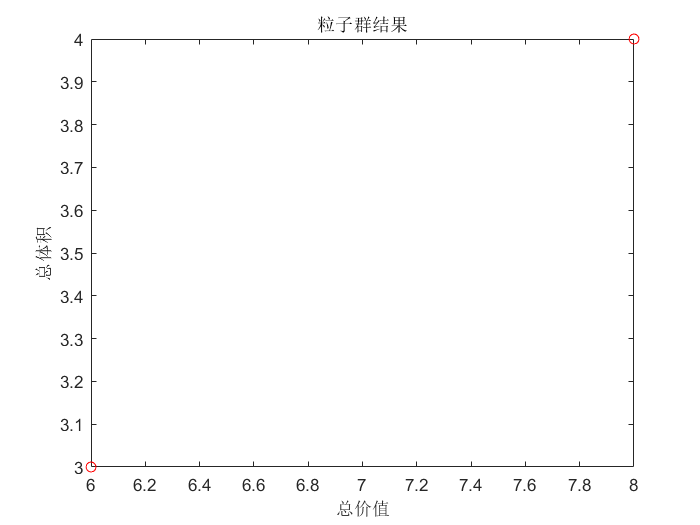
可以看到总价值8和总体积4的粒子(背包)是最优背包,符合我们最开始穷举的结论。
三:粒子群算法解其他背包问题
3.1 分组背包每组最多选一个物品
当求解分组背包问题的另一种情况:每组物品最多选一个,也就是每组物品可选可不选时,我们可以把输入参数矩阵做如下个小处理,添加1个物品,其价值、体积、质量都置为0就可以了。
P:
| 物品/分组 | 第一组 | 第二组 | 第三组 |
|---|---|---|---|
| 物品1价值 | 1 | 2 | 3 |
| 物品2价值 | 3 | 2 | 1 |
| 物品3价值 | 0 | 0 | 0 |
V:
| 物品/分组 | 第一组 | 第二组 | 第三组 |
|---|---|---|---|
| 物品1体积 | 1 | 2 | 1 |
| 物品2体积 | 2 | 1 | 2 |
| 物品3体积 | 0 | 0 | 0 |
M:
| 物品/分组 | 第一组 | 第二组 | 第三组 |
|---|---|---|---|
| 物品1质量 | 20 | 50 | 40 |
| 物品2质量 | 30 | 40 | 20 |
| 物品3质量 | 0 | 0 | 0 |
3.1 01背包问题
01背包是没有分组,每个物品最多选一次,那就当成分组背包的一个特例。每个物品都属于一个组,每一组的输入参数矩阵再添加1个物品,其价值、体积、质量都置为0也就可以了。
P:
| 物品/分组 | 第一组 | 第二组 | 第三组 | 第四组 | 第五组 | 第六组 |
|---|---|---|---|---|---|---|
| 物品1价值 | 1 | 2 | 3 | 1 | 2 | 3 |
| 物品2价值 | 0 | 0 | 0 | 0 | 0 | 0 |
V:
| 物品/分组 | 第一组 | 第二组 | 第三组 | 第四组 | 第五组 | 第六组 |
|---|---|---|---|---|---|---|
| 物品1体积 | 1 | 2 | 1 | 2 | 1 | 2 |
| 物品2体积 | 0 | 0 | 0 | 0 | 0 | 0 |
M:
| 物品/分组 | 第一组 | 第二组 | 第三组 | 第四组 | 第五组 | 第六组 |
|---|---|---|---|---|---|---|
| 物品1质量 | 20 | 50 | 40 | 30 | 40 | 20 |
| 物品2质量 | 0 | 0 | 0 | 0 | 0 | 0 |
四:常规DP算法解分组背包问题
分组背包题目
4.1 C++ 常规DP解法
#include <iostream>
using namespace std;
int v[110][110],w[110][110],s[110];
int f[110];
int main()
{
int N,V;
cin >> N >> V;
for (int i = 1; i <= N; i ++)
{
cin >> s[i];
for (int j = 1; j <= s[i]; j ++)
cin >> v[i][j] >> w[i][j];
}
for (int i = 1; i <= N; i ++)
for (int j = V; j > 0; j --)
for (int k = 1; k <= s[i]; k ++)
if (j >= v[i][k])
f[j] = max(f[j],f[j - v[i][k]] + w[i][k]);
cout << f[V];
return 0;
}
/*
输入:
3 5
2
1 2
2 4
1
3 4
1
4 5
输出:
8
*/
4.2 MATLAB 粒子群解法
这道题目中少了一个重量的维度。我们只用把上面粒子群程序的输入矩阵改为如下形式,然后把对重量的限制改为对体积的限制就好了。
P = [2 4 5; 4 0 0; 0 0 0]; % 各组物品价值
V = [1 3 4; 2 0 0; 0 0 0]; % 各组物品体积
weight = 5; % 背包最大体积限制
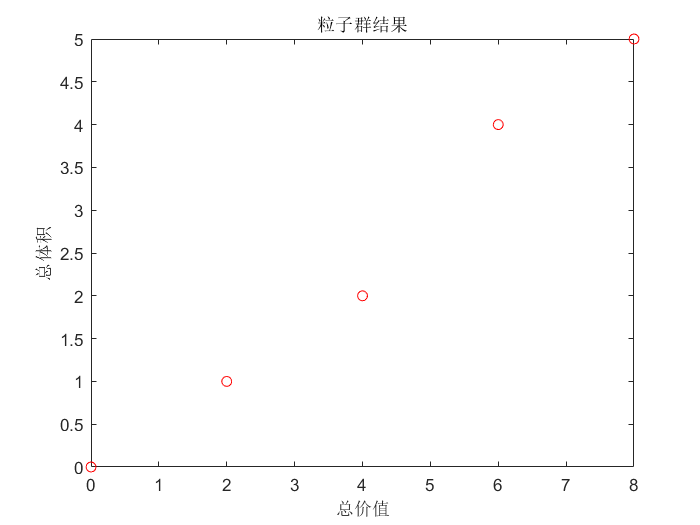
可以看到总价值最高的粒子(背包)也是8。
五:参考文献
[1] 郁磊,史峰,王辉,等.MATLAB智能算法30个案例分析(第2版)[M].北京:北京航空航天大学出版社,2015.