1 概述
机器视觉就是用机器代替人眼和人脑来做测量和判断。机器视觉系统工作的基本过程是获取目标的图像后,对图像进行识别、特征提取、分类、数学运算等分析操作,并根据图像的分析计算结果,来对相应的系统进行控制或决策的过程。
在很多机器视觉应用中,都需要用到机器视觉测量,即根据目标的图像,来得到目标在实际空间中的物理位置,最典型的如行走机器人、SLAM等。
要根据图像中的目标像素位置,得到目标的物理空间位置,我们需要首先有一个图像像素坐标与物理空间坐标的映射关系,也就是将光学成像过程抽象为一个数学公式,这种能够表达空间位置如何映射到图像像素位置的数学公式,就是所说的机器视觉成像模型,本文即讨论这种模型的机理。
2 小孔成像
机器视觉成像采用小孔成像模型,如下图所示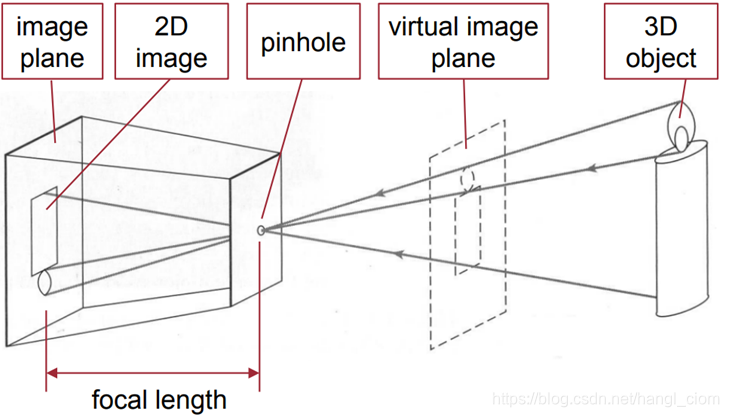
再次简化为下图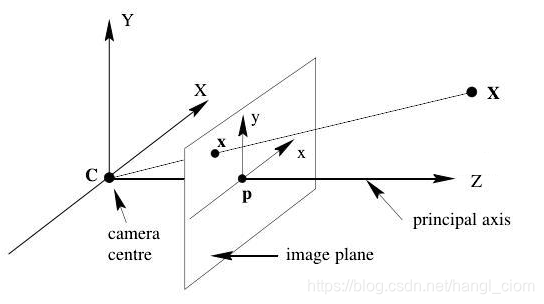
图中X 是一个空间点,x 为该空间点在图像中的成像点,C 为镜头光心(camera centre),从图中可看到,C 、x 、X 三个点是共线的。
光心C 距离成像面(image plane)的距离即焦距f 。
后面的各个坐标系及其相互关系都是基于这个小孔成像模型推出。
3 坐标系
说到机器视觉测量模型,就少不了先要了解整个模型中涉及的几个坐标系。
3.1 像素坐标系uov
即图像中各像素点坐在的坐标系,如下图所示uov。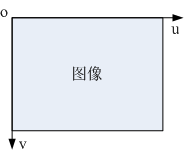
这个坐标系是一个二维坐标系,横坐标为图像宽度方向,纵坐标为图像高度方向,原点位于左上角,坐标轴单位为像素,与图像的像素点对应。
3.2 图像坐标系xoy
即图像传感器(如CMOS、CCD)坐标系,如下图所示xoy。
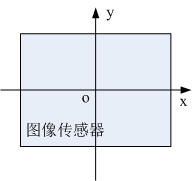
这个坐标系同样是一个二维坐标系,横坐标为传感器宽度方向,纵坐标为传感器高度方向,原点位于传感器中心,坐标轴单位为mm(根据实际需要设定,m、mm、……),后面的坐标系也都是同样单位,不再说明。
结合像素坐标系,我们可以得到下图
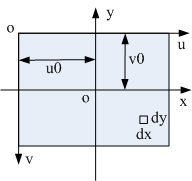
从此图中,我们可以得到像素坐标系uov与图像坐标系xoy的映射关系,即:

式中:
u 0 、v 0 ——图像中心像素点坐标(通常为图像横纵向分辨率的一半,但如果镜头与传感器位置装偏了,就不是一半了),单位pixel;
d x 、dy——传感器单元的横纵向尺寸(即像元尺寸),单位mm/pixel,通常像元是正方形,就有dx=dy
上式写成齐次矩阵形式,就是像素坐标系与图像坐标系的转换关系

注意到以上公式中y方向加了个负号,是因为像素坐标系uov是个左手坐标系,但后面要讨论的三维坐标系都是采用右手坐标系,所以这里图像坐标系xoy直接设置为右手坐标系,负号是用来转换y轴方向。
3.3 相机坐标系O C X C Y C Z C
在相机镜头上设置一个三维坐标系,如下图,原点位于光心,X轴与Y轴分别与图像坐标系的x和y轴平行,Z轴指向物方。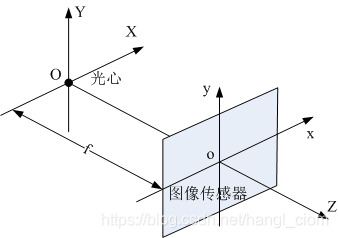
根据前文的小孔成像模型,我们可以得到YOZ(YCZ)平面里的投影关系,如下图(XOZ平面同理)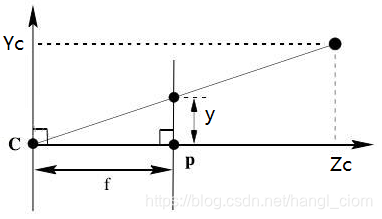
上图中,根据相似三角形,有![]() ,因而可以写出相机坐标系与图像坐标系的转换关系,我们直接写为齐次坐标形式
,因而可以写出相机坐标系与图像坐标系的转换关系,我们直接写为齐次坐标形式

式中:f ——镜头焦距,有的文献里公式会把焦距分为X和Y向的f x 、f y代入前文的像素坐标系与图像坐标系的转换公式

我们可以得到相机坐标系与像素坐标系的转换关系如下

我们用M 1

这个矩阵中的参数只与镜头焦距f 、像元尺寸dxdy、中心像素u 0 v 0有关,这都是相机和镜头的内部参数,相机及镜头确定后这个矩阵就被确定,所以被称为内参矩阵。
3.4 世界坐标系OWXWYWZW
世界坐标系是系统的绝对坐标系,同样是三维坐标系,原点及坐标轴方向根据我们需要来选定。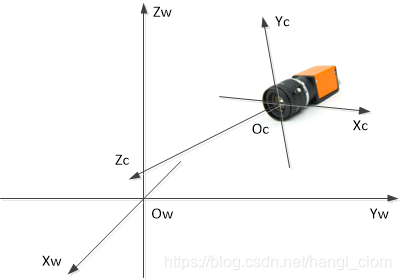
相机作为一个刚体,在世界坐标系中具有位姿——位置和姿态,位置即为相机(相机坐标系原点)相对于世界坐标系原点的平移,用一个3×1平移向量T C 表达,姿态即为相机(相机坐标系)相对于世界坐标系的旋转,用一个3×3旋转矩阵R C 表达那么我们就可以得到相机坐标系与世界坐标系的关系

反过来

这就是世界坐标系与相机坐标系的转换关系,其中的矩阵M 2 与相机的位姿有关,称为外参矩阵。
代入前文的像素坐标系与相机坐标系的转换公式,得到

4 机器视觉投影矩阵
至此,我们就得到了像素坐标系与世界坐标系的映射关系,即机器视觉投影矩阵

其中:
Z C ——空间点在相机坐标系中的Z坐标
M 1——内参矩阵,3×4矩阵
M2——外参矩阵,4×4矩阵,




