背包问题是动态规划最具有代表性的问题。问题是这样的：

问题

法外狂徒张三是一个探险家，有一次巧合之下进入到一个有宝藏的洞穴里。这个洞穴有很多个不重复的宝贝，同时每个宝贝的重量也不一样。具体来说有：
A 重 2 价值为 2
B 重 3 价值为 6
C 重 4 价值为 4
D 重 4 价值为 5
E 重 1 价值为 3
现在张三就只有一个背包，这个背包承重为10，张三想知道如何装才能带走价值最大的宝藏？

原理

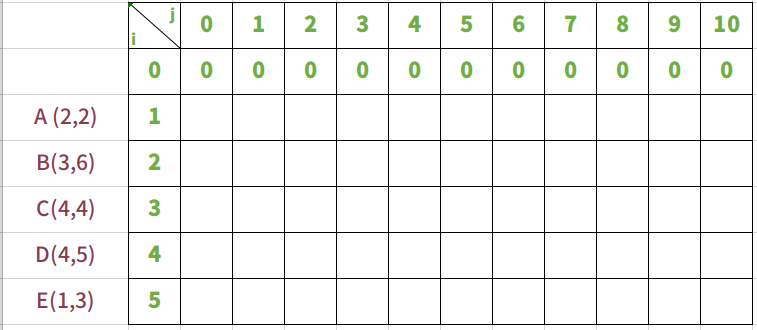
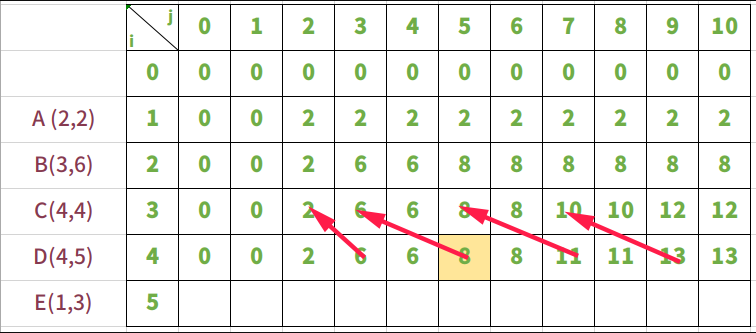
在这个问题里其实有两个变量，第一：物品 ABCDE，是一种变量；第二：背包的承重为另个变量。所以首先假设一种最极端的状态：物品只有0个，背包的重量也为0。这就是边界值

以背包的承重量为变量，从0到10，在物品只有0个情况下，背包的最大价值。

0 0 0 0 0 0 0 0 0 0 0 0

关于背包的价值和物品的重量之间有一个关系，那就是背包放物品，如果承重大于物品的重量，则放入，背包的价值增加，相应的背包的承重减少。如果承重小于物品，则放不进去，背包承重不变，价值不变。那么到底这个物品放不放呢？主要取决于该物品放了背包的价值和物品不放背包的价值哪个大？（放物品的价值可不一定大于不放，因为这个相对于全局来说的）

• 假设变量 j 为背包的容量，i表示第i个物品，weight[i]表示i物品的重量， value[i]表示i物品的价值,bag[i][j]表示在放入第i个物品时，背包容量为j时的背包价值。那么会有一个表达式用于选择：

• 如果背包容量j小于物品i的重量，放不进物品，背包的价值等于之前物品放入的价值。所以：bag[i][j] = bag[i-1][j]
  如果背包的容量j大于物品i的重量，能够放入物品，那么要不要放则取决于背包放入物品时价值大还是不放入价值大所以： bag[i][j] = max(bag[i-1][j-weight[i]] + value[i] , bag[i-1][j])

为什么是前一行?
因为前一行是到达当前重量时背包内物品的最大价值，如果选择不放当前物品，说明背包容量不够，那么现在的最大价值只能是前一行的值。同理，选择放当前物品，那么也应该在前一行的基础上加上当前物品的价值。

不放入任何物品时，背包承重从0到10

当物品为0时，背包的承重从0到10变化，其价值一直不变，始终都是0

放入物品A，背包承重从0到10

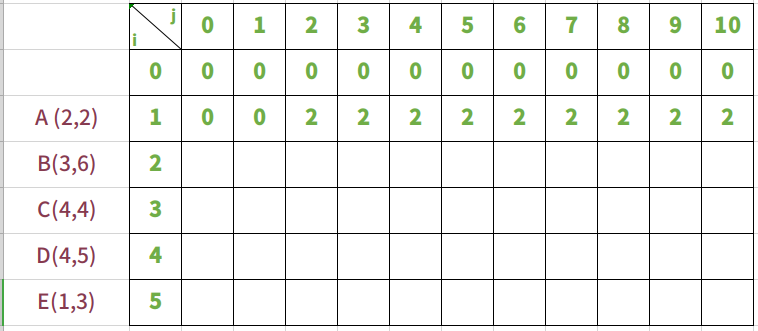
放入物品A时，只有一个物品，所以逻辑很简单。当背包重量能够装下A的重量2时，背包就放入A，价值就变成2。后面无论背包承重如何变化，价值都不变。

放入物品B，背包承重从0到10

当放入物品B时，其实是在背包放入A的前提下进行的。

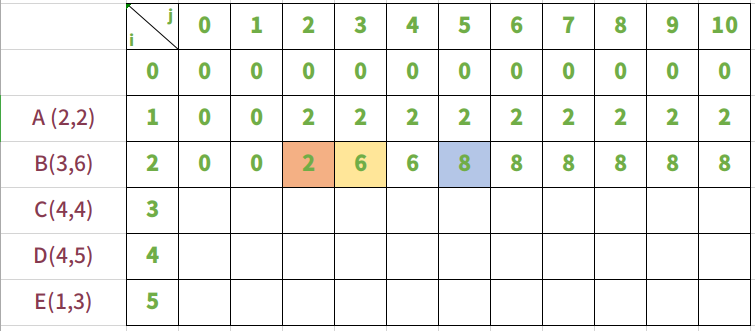
下面来一点点算出来，为什么放入物品B时，重量变化是这样。

i=2,j=2, j还不能放入物品B，所以bag=bag[i-1][j] 即 bag[1][2]=2
i=2,j=3, j刚好能放入物品B，所以bag= max(bag[i-1][j-weight[i]] + value[i] , bag[i-1][j]),即bag = max(bag[1][0]+6,bag[1][3])==>bag = max(6,2)。所以bag[1][3] = 6 。放入物品B价值大
i=2,j=4, j能放入物品B，所以同上bag = max(bag[1][1]+6,bag[1][4]) ==> bag = max(6,2)。所以bag[1][4] = 6。放入物品B价值大
i=2,j=5, j能放入物品B，所以bag = max(bag[1][2]+6,bag[1][5]) ==> bag = max(8,2)。所以bag[1][5] = 8。放入物品B价值大。在背包重量j=5时，能够先放入B，然后再放入A。
i=2,j=6, 同上
i=2,j=7, 同上
i=2,j=8, 同上
i=2,j=9, 同上
i=2,j=10, 同上

放入物品C，背包承重从0到10

放入物品C时，其实是在背包中放入A和B的假设前提下进行的。

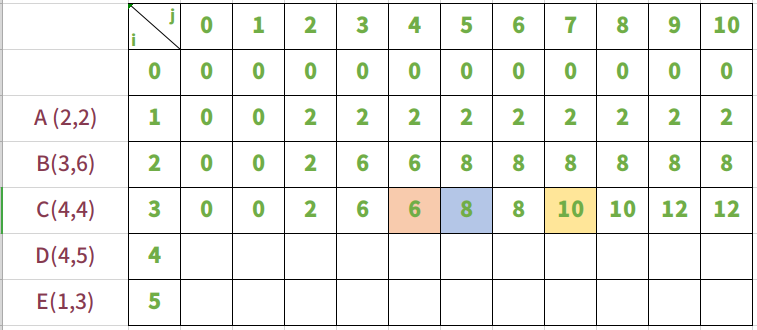
按照正常的规律去算。其中需要主要的是j=4、j=5时。
i=4,j=4 ,背包能够放入物品C。bag = max(bag[4-1][4-4]+4,bag[4-1][4]) ==> bag = max(4,6)。所以bag[4][4] = 6。这里不再是放入物品C背包价值大，而是不放入时价值更大。
i=4,j=5 ,背包能够放入物品C。bag = max(bag[4-1][5-4]+4,bag[4-1][5]) ==> bag = max(4,6)。所以bag[4][5] = 6。同样，这里不放入物品C背包价值更大。
i=4,j=7 , 背包能够放入物品C。bag = max(bag[4-1][7-4]+4,bag[4-1][7]) ==> bag = max(6+4,8)。所以bag[4][7] = 10。这里放入物品C背包价值更大。

放入物品D，背包承重从0到10

放入物品D时，是在假设放入ABC的基础上进行。

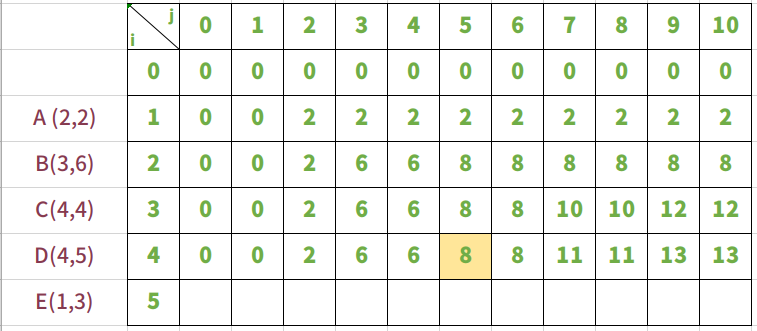
需要注意的是当i=4,j=5时
i=4,j=5,背包能够放入物品D，bag = max(bag[4-1][5-5]+4,bag[4-1][5]) ==> bag = max(4,8)。所以bag[4][5] = 8。同样，这里不放入物品D背包价值大。

放入物品E，背包承重从0到10

放入物品E时，是在放入ABCD的前提下进行的。

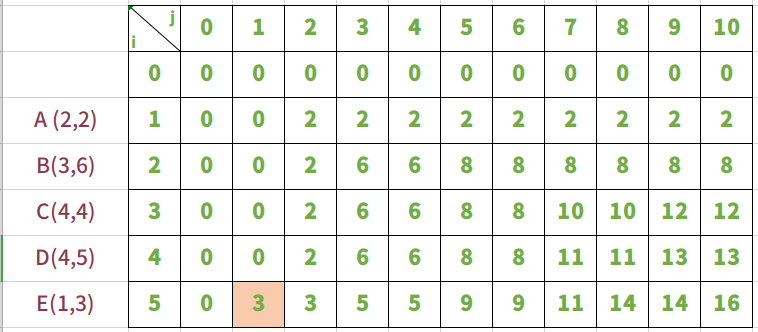
最后一个放入物品E。
i=5,j=1,背包刚好能够放入物品E。这是bag = max(bag[5-1][1-1]+3,bag[5-1][1]) ==> bag = max(3,0)。所以bag[5][1] = 3。这是放入物品E背包价值大

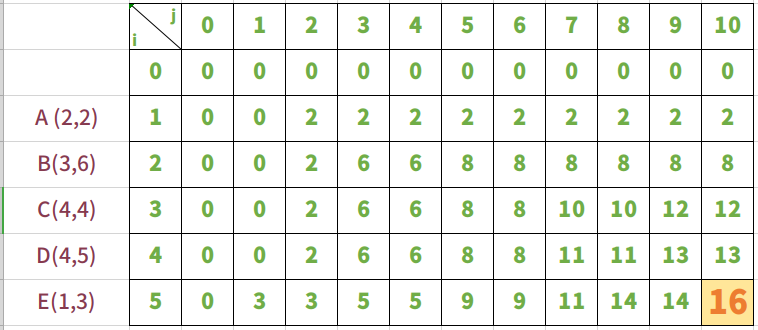
结果

最终获得放入ABCDE五种物品的结果，也就是bag[5] 这一行的价值。最后当bag的承重为10时，最大的价值为16。所以16就是我们要求的价值。

代码实现

背包最大价值

weight = [0,2,3,4,4,1]
value = [0,2,6,4,5,3]
weight_most=10

bag = [[0 for i in range(weight_most+1)] for j in range(len(weight))]

for i in range(1,len(weight)):
    for j in range(1,weight_most+1):
        if j >= weight[i]:
            bag[i][j] = max(bag[i-1][j-weight[i]]+value[i],bag[i-1][j])
        else:
            bag[i][j] = bag[i-1][j]

print(bag[-1][-1])

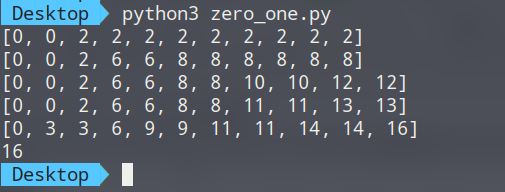
找到背包里的物品

weight = [2,3,4,4,1]
value = [2,6,4,5,3]
weight_most=10

dp = [0] * (weight_most+1)

for i in range(len(weight)):
    for j in range(weight_most,weight[i]-1,-1):
        dp[j] = max(dp[j-weight[i]]+value[i], dp[j])

print(dp)

01背包问题优化

01背包的时间复杂度已经无法优化，但是在空间复杂度上还存在优化的可能。
观察以上二维数组推导的过程，可以发现一个规律：当前这一行的的数据只和上一层数据有关。进一步观察，可以发现是和上一层数据的前面的列有关

所以能否将二维数组转化为一维数组呢？答案是可以的。使用一维数组时，当前数组保存的是上一次的结果，那么下一次的结果就直接写入数组就能完成数据的查找和写入。
但是需要从后往前遍历和填值。因为后面的值依赖于前面的值，如果前面的值改变了，后面的依赖就不准确。

weight = [0,2,3,4,4,1]
value = [0,2,6,4,5,3]

weight_most=10

# 使用一维数组完成记录
bag = [0 for i in range(weight_most+1)]
for i in range(1,len(weight)):
    # 从后向前遍历，因为后面的值依赖前面的值，从后向前不会破坏前面的值，就不会破坏后面的依赖
    for j in range(weight_most,0,-1):
        if j >= weight[i]:
            bag[j] = max(bag[j-weight[i]]+value[i],bag[j])    
print(bag[-1])

贪心算法

贪心算法（又称贪婪算法）是指，在对问题求解)时，总是做出在当前看来是最好的选择。也就是说，不从整体最优上加以考虑，他所做出的是在某种意义上的局部最优解。

动态规划和贪心算法都是一种递推算法 即均由局部最优解来推导全局最优解

过程：
动态规划算法将每个子问题求解一次，将其解保存在一个表格中，需要时进行调用。

特征：
刻画一个最优解的结构特征。
递归的定义最优解的值。

计算最优解的值，有自顶向下和自底向上的方法，通常采用自底向上的方法。

DP思想：

1、把一个大的问题分解成一个一个的子问题。
2、如果得到了这些子问题的解，然后经过一定的处理，就可以得到原问题的解。
3、如果这些子问题与原问题有着结构相同，即小问题还可以继续的分解。
4、这样一直把大的问题一直分下去，问题的规模不断地减小，直到子问题小到不能再小，最终会得到最小子问题。
5、最小子问题的解显而易见，这样递推回去，就可以得到原问题的解。

与贪心法的区别：不是由上一步的最优解直接推导下一步的最优解，所以需要记录上一步的所有解

贪心算法：

每一步都做出当时看起来最佳的选择，也就是说，它总是做出局部最优的选择。
贪心算法的设计步骤：

• 对其作出一个选择后，只剩下一个子问题需要求解。
• 证明做出贪心选择后，原问题总是存在最优解，即贪心选择总是安全的。
• 剩余子问题的最优解与贪心选择组合即可得到原问题的最优解。

与动态规划的区别：贪心算法中，作出的每步贪心决策都无法改变，由上一步的最优解推导下一步的最优解，所以上一部之前的最优解则不作保留。

能使用动态规划算法的条件：

如果一个问题被划分各个阶段之后，阶段I中的状态只能由阶段I-1中的状态通过状态转移方程得来，与其它状态没有关系，特别是与未发生的状态没有关系，那么这个问题就是“无后效性”的，可以用动态规划算法求解