本文我们继续讨论拟合优度检验的相关问题。由于本系列为我独自完成的,缺少审阅,如果有任何错误,欢迎在评论区中指出,谢谢!
目录
- Part 1:分布未知的Pearson $\chi^2$检验
- Part 2:列联表
- Section 1:独立性检验
- Section 2:齐一性检验
- Part 3:正态性检验
- 附录
- 1、chisq.independence(mat)
- 2、chisq.consistency(mat, prob)
- 3、绘制QQ图
Part 1:分布未知的Pearson \(\chi^2\)检验
在上篇文章中我们讲到了分布已知的Pearson \(\chi^2\)检验,这是将观测值分成\(r\)个组,根据实际频数\(\nu_i\)和理论频数\(np_i\)计算\(\chi^2\)统计量
\[K_n=\sum_{i=1}^r\frac{(\nu_i-np_i)^2}{np_i}, \]
将其近似为\(\chi^2_{r-1}\)分布给出拟合优度。其条件是,每一个\(p_i\)都是已知的,如上例中孟德尔豌豆实验的\(9:3:3:1\),或者具体地服从参数为\(3\)的泊松分布,等等。
现在我们要讨论的问题是,给定一定的样本,要检验的问题是:它是否服从某一特定的分布族,如泊松分布族、均匀分布族、正态分布族,等等。它与上文中所讨论的情况区别在于,此时不知道每一个具体的\(p_i\)是多少,自然就不能计算\(np_i\)是多少。
对于参数分布族而言,它们的未知性完全由少数几个参数决定,这就给我们的拟合优度检验提供了思路:如果我们能把这些参数变成已知量,那么\(p_i\)就已知了,可以照常使用Pearson \(\chi^2\)检验。因此,如果给定了分布族但没有给定具体的分布,则我们可以先估计出未知参数来。
这里使用的估计方法是点估计,我们选择普适性更强的极大似然估计,对分布族\(f(x;\theta)\),在给定样本的情况下,可以先给出\(\theta\)的极大似然估计\(\hat\theta\),从而将分布变为具体的\(f(x;\hat\theta)\),再执行适当的分组让各个\(p_i\)已知,计算\(\chi^2\)统计量。
这里的极大似然估计并不是样本的极大似然估计,而是对划分区间的极大似然估计,具体地,设\(\nu_j\)为样本\(X_1,\cdots,X_n\)中归类为第\(j\)类的个数,则似然函数为
\[L=\frac{n!}{\nu_1!\cdots\nu_r!}(p_1(\theta))^{\nu_1}\cdots(p_r(\theta))^{\nu_r}, \]
对\(\ln L\)关于\(\theta\)求导(如果\(\theta\)是多维的,则是对向量求导),得到方程:
\[\sum_{i=1}^r \frac{\nu_i}{p_i(\theta)}\cdot\frac{\partial p_i(\theta)}{\partial\theta}=0, \]
由此方程解出的\(\hat\theta\)是我们这里所需要的极大似然估计,它与由样本直接计算的极大似然估计是不一样的。
不过,需要注意的是,由于参数使用了估计量,所以\(\chi^2\)统计量尽管计算方法相同,但却不再具有\(\chi^2_{r-1}\)的极限分布。Fisher指出:若存在参数空间\(\Theta\)的\(s\)维内点\(\theta\),使得\(X\)的分布为\(F(x;\theta)\),则对于\(\theta\)的相合估计量\(\hat\theta\),在原假设成立的情况下,有
\[K_n\stackrel{d}\to \chi^2_{r-1-s}. \]
一般,矩估计不能用于待估参数的估计,寻找待估参数\(\hat\theta\)可以使用最小\(\chi^2\)法,即定义
\[K_n(\theta)=\sum_{i=1}^n\frac{(\nu_i-np_i(\theta))^2}{np_i(\theta)}, \]
寻找使得\(K_n(\theta)\)最小也就是偏离量最小的\(\theta\)作为参数估计,即求解
\[\frac{\partial K_n(\theta)}{\partial \theta}=0. \]
这个方程组很难解。
使用极大似然法,将\(\theta\)关于划分区间的极大似然估计作为估计值会更简单一些,并且也满足条件。但是这个方程组也不是很容易求解。
为图方便,我们可能会想着直接用样本的极大似然估计(如正态分布中的\(\bar X\)和\(\frac{n-1}{n}S^2\))来作为\(\theta\)的估计量,这样计算量就小得多。但是此时\(K_n(\theta)\)不一定有极限分布\(\chi^2_{r-1-s}\),更确切地说来,此时的拟合优度真值是介于\([\mathbb{P}(\chi^2_{r-s-1}\ge k_0),\mathbb{P}(\chi^2_{r-1}\ge k_0)]\)之间的。
关于这部分的内容,不再详细展开,如果能够计算出参数的估计值,就自然可以算出各个区间的概率,然后用pearson.chi2()函数即可计算。不过要注意,此时只有\(K_n\)的计算值是可用的,拟合优度需要用\(\chi^2_{r-s-1}\)的分布来计算。
Part 2:列联表
列联表指的是将每一个样本的两类指标\(A\)和\(B\)作统计,进而判断两个指标之间是否存在一定的关系,典型例子就是吸烟和肺癌之间的关联。具体地,列联表相关的问题又可以分为独立性检验与齐一性检验,它们都可以使用\(\chi^2\)检验来完成,与拟合优度检验类似,又有所不同。
Section 1:独立性检验
独立性检验指的是,判断某个个体的两项指标\(A,B\)是否相关。一般地,可以将一个由大量个体构成的总体按照指标\(A\)划分成\(r\)级:\(A_1,\cdots,A_r\),按照指标\(B\)划分成\(s\)级:\(B_1,\cdots,B_s\),第\(i\)个个体的指标状况为\((A_{r_i},B_{s_i})\)。
这将第\(i\)个个体看成随机向量\(X_i\),就有\(X_i=(r_i,s_i)\)。如果不同个体之间相互独立,就可以将\(n\)个个体\(X_1,\cdots,X_n\)视为\(n\)个从总体\(X\)中抽取的简单随机样本,指标\(A,B\)无关就意味着\(X=(X^{(1)},X^{(2)})\)的两个分量\(X^{(1)},X^{(2)}\)相互独立。记
\[p_{ij}=\mathbb{P}(X^{(1)}=i,X^{(2)}=j),\quad \forall i=1,\cdots,r;j=1,\cdots,s. \]
则\(X^{(1)},X^{(2)}\)独立的充要条件是:存在\(p^{(1)}_1,\cdots,p_r^{(1)}\)和\(p_1^{(2)},\cdots,p_s^{(2)}\ge 0\)使得
\[\sum_{i=1}^r p_i^{(1)}=1,\quad \sum_{j=1}^s p_j^{(2)}=1,\\ p_{ij}=p_i^{(1)}\cdot p_j^{(2)},\quad \forall i=1,\cdots,r;j=1,\cdots,s. \]
这样便定义了一个含参数的拟合优度检验问题,完成了模型的转化,接下来的推导步骤请尽可能理解,如果难以理解也可以直接记住结论。
对于列联表而言,令\(n_{ij}\)为\(X^{(1)}=i,X^{(2)}=j\)的样本个数,则可以作出这样的列联表:
\[\begin{matrix} & 1 & \cdots & j & \cdots & s \\ 1 & n_{11} & \cdots & n_{1j} & \cdots & n_{1s} & n_{1\cdot} \\ \vdots & \vdots & & \vdots & & \vdots & \vdots \\ i & n_{i1} & \cdots & n_{ij} & \cdots & n_{is} & n_{i\cdot} \\ \vdots & \vdots & & \vdots & & \vdots & \vdots \\ r & n_{r1} & \cdots & n_{rj} & \cdots & n_{rs} & n_{r\cdot} \\ & n_{\cdot 1} & \cdots & n_{\cdot j} & \cdots & n_{\cdot s} & n \end{matrix} \]
计算表明,应当用\(n_{i\cdot}/n\)来作为\(p_i^{(1)}\)的估计值,\(n_{\cdot j}/n\)来作为\(p_j^{(2)}\)的估计值,于是计算所得的\(\chi^2\)统计量为
\[K_n=\sum_{i=1}^r\sum_{j=1}^s\frac{\left(n_{ij}-n\hat p_i^{(1)}\hat p_j^{(2)}\right)^2}{n\hat p_i^{(1)}\hat p_j^{(2)}}=n\left(\sum_{i=1}^r\sum_{j=1}^s\frac{n_{ij}^2}{n_{i\cdot}n_{\cdot j}}-1 \right). \]
在独立性假设成立的情况下,\(K_n\)应当渐进服从自由度为
\[rs-1-(r+s-2)=(r-1)(s-1) \]
的\(\chi^2\)分布。
R语言中有可以直接用于独立性检验的函数,但是计算结果与我们实际的计算式略有不同,因此我们自编一个
chisq.independence()函数进行独立性检验,代码见附录。> mat <- matrix(c(442, 38, 514, 6), nrow=2) > chisq.independence(mat) Pearson chi2 independence test The value of K: 27.13874 p-value: 1.893646e-07此时
p-value远小于\(0.05\),所以认为独立性假设不成立。
特别在\(r=s=2\)时(考试可能出到的范围),以下公式有助于简化计算\(K_n\)的值:
\[K_n=\frac{n(n_{11}n_{22}-n_{12}n_{21})^2}{n_{1\cdot}n_{2\cdot}n_{\cdot 1}n_{\cdot 2}}. \]
这是我们在高中时常用的计算式,而高中常用到的\(3.841\)就是自由度为\(1\),\(\alpha=0.05\)时的临界值。
Section 2:齐一性检验
齐一性检验的提法是\(r\)个工厂\(A_1,\cdots,A_r\)生产的产品可以分为\(B_1,\cdots,B_s\)的\(s\)个等级,第\(i\)个工厂的\(j\)等品率为\(p_i(j)\),要验证的假设是\(r\)个工厂产品质量相同,即
\[p_1(j)=\cdots =p_r(j),\quad \forall j=1,\cdots,s. \]
齐一性检验与独立性检验略有不同,其关键不同就在于此时\(A_1,\cdots,A_r\)的\(r\)个工厂中抽取的产品数不是随机的,而是可以自由挑选的,也就是说\(n_{i\cdot}\)是事先选定的而非随机的。这一点关键的不同带来的问题是\(\chi^2_{(r-1)(s-1)}\)的极限分布是否依然存在,但幸好,有结论表明,极限分布依然是\(\chi^2_{(r-1)(s-1)}\)。对于这种情况,chisq.independence(mat)函数依然适用。
齐一性检验中还有一种情况,就是\(j\)等品的分布是已知的,即要验证的假设增加为
\[p_1(j)=\cdots=p_r(j)=p_j^0,\quad \forall j=1,\cdots,s. \]
此时,未知参数只剩下\(p_{1}^{(1)},\cdots,p_{r}^{(1)}\),因而极限分布的自由度应该是\((rs-1)-(r-s)=r(s-1)\),\(K_n\)的计算式也自然变成了
\[K_n=\sum_{i=1}^r\sum_{j=1}^s\frac{(n_{ij}-n_{i\cdot}p_j^0)^2}{n_{i\cdot}p_j^0}\stackrel{d}\to \chi^2_{r(s-1)}. \]
类似编写了chisq.consistency(mat, prob)函数用于应对这种情况,不过由于书上没有给出相关例题,我也难以保证这个函数的运行结果是\(100\%\)正确的。
Part 3:正态性检验
正态性检验是检验数据是否服从正态分布的,理论上Pearson \(\chi^2\)检验和柯氏检验都可以完成这个任务。我们将其单独拿出来讨论,是因为正态分布是一种重要的分布,故需要一些更有针对性的检验,而不是使用适用面广的检验。
小样本下,正态性检验的方法是\(W\)检验;大样本下,正态性检验的方法是\(D\)检验。其原理我们不详述,以下给出R语言中,如何使用这两种检验方法进行正态性检验。
\(W\)检验又叫Shapiro-Wilk检验,在R中的函数为shapiro.test()。其原假设是\(H_0\):\(X\)服从正态分布,计算出的\(W\)统计量越大,正态性越强,越应该接受原假设。尽管我们还没有介绍什么是检验的p-value,不过读者只需要知道,p-value越大越应该接受原假设,如果p-value小于给定的阈值\(\alpha\)(可以取\(0.05\))就拒绝原假设。以下以书上的例子为例给出\(W\)检验的实例。
> v <- c(57, 66, 74, 77, 81, 87, 91, 95, 97, 109)
> shapiro.test(v)
Shapiro-Wilk normality test
data: v
W = 0.99134, p-value = 0.9982
\(D\)检验又叫D ‘Agostino检验,在R语言的fBasics包中提供了dagoTest()函数:
> dagoTest(runif(100))
Test Results:
STATISTIC:
Chi2 | Omnibus: 26.2949
Z3 | Skewness: -0.3753
Z4 | Kurtosis: -5.1141
P VALUE:
Omnibus Test: 1.95e-06
Skewness Test: 0.7074
Kurtosis Test: 3.152e-07
可以看到,我们使用均匀分布随机数时,综合性检验、偏度检验、峰度检验有两项都不能通过正态性检验。
还有一种直观的检验方法:Q-Q图检验,其原理是将要检验的样本的次序统计量,按照正态分布的分布函数反函数绘制到一张图上,如果这个散点图近似呈现一条直线,则认为这个样本服从正态分布。当然,这种方法有些主观,主要依靠人眼,不过由于十分直观,许多人也喜欢使用这个方法。
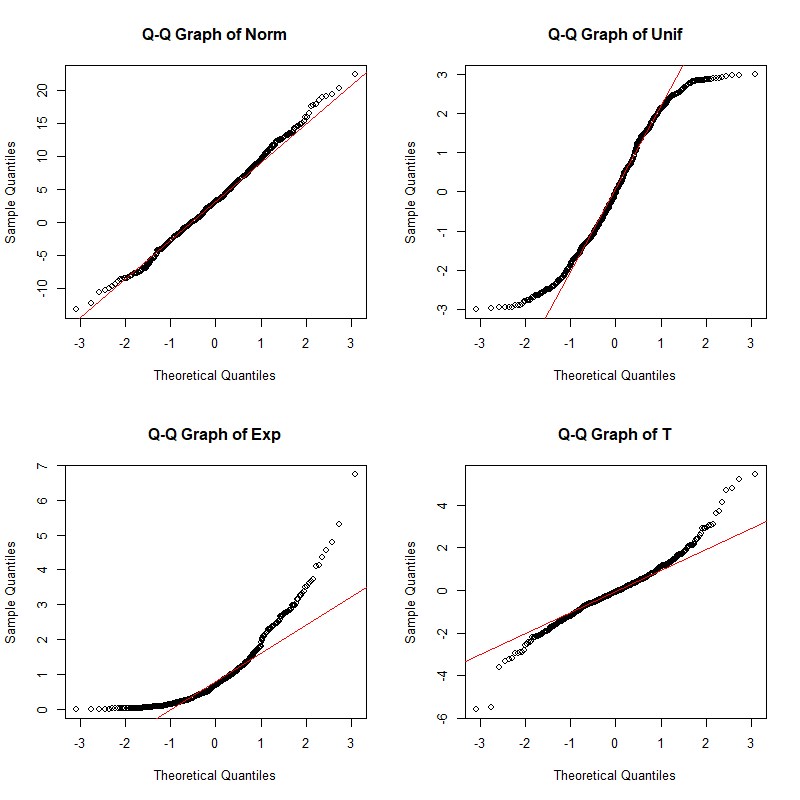
拟合优度检验属于一种非参数假设检验,包括列联表中的相关问题。下一篇文章,我们将回到参数假设检验问题上,讨论正态分布参数的假设检验,这也是我们最常遇到的问题。
附录
1、chisq.independence(mat)
chisq.independence <- function(mat){
rt <- list()
r <- nrow(mat)
s <- ncol(mat)
if (r == 1 || s == 1){
cat("错误:矩阵维度过低")
return(None)
}
rt$rows <- r
rt$cols <- s
sumrow <- apply(mat, 1, sum)
sumcol <- apply(mat, 2, sum)
n <- sum(mat)
rt$sumrow <- sumrow
rt$sumcol <- sumcol
rt$total <- n
K <- 0
for (i in 1:r){
for (j in 1:s){
K = K + mat[i, j]^2 / (sumrow[i] * sumcol[j])
}
}
K = n * (K - 1)
rt$X.square <- K
p.value <- 1 - pchisq(K, df=(r-1)*(s-1))
rt$p.value <- p.value
cat("\n\tPearson chi2 independence test\n\n")
cat("The value of K: ", K, "\n")
cat("p-value: ", p.value, "\n")
lst <- rt
}
2、chisq.consistency(mat, prob)
chisq.consistency <- function(mat, prob){
rt <- list()
r <- nrow(mat)
s <- ncol(mat)
if (s == 1){
cat("错误:矩阵维度过低")
return(None)
}
rt$rows <- r
rt$cols <- s
prob <- prob / sum(prob)
rt$prob <- prob
sumrow <- apply(mat, 1, sum)
sumcol <- apply(mat, 2, sum)
n <- sum(mat)
rt$sumrow <- sumrow
rt$sumcol <- sumcol
rt$total <- n
K <- 0
for (i in 1:r){
for (j in 1:s){
K = K + (mat[i, j] - sumrow[i] * prob[j])^2 / (sumrow[i] * prob[j])
}
}
rt$X.square <- K
p.value <- 1 - pchisq(K, df=r*(s-1))
rt$p.value <- p.value
cat("\n\tPearson chi2 consistency test\n\n")
cat("The value of K: ", K, "\n")
cat("p-value: ", p.value, "\n")
lst <- rt
}
3、绘制QQ图
rm(list=ls())
dev.off()
opar <- par(no.readonly = T)
par(mfrow = c(2,2))
x1 <- rnorm(500, 3, 6)
qqnorm(x1, main = "Q-Q Graph of Norm")
qqline(x1, col = "red")
x2 <- runif(500, -3, 3)
qqnorm(x2, main = "Q-Q Graph of Unif")
qqline(x2, col = "red")
x3 <- rexp(500, 1)
qqnorm(x3, main = "Q-Q Graph of Exp")
qqline(x3, col = "red")
x4 <- rt(500, 5)
qqnorm(x4, main = "Q-Q Graph of T")
qqline(x4, col = "red")