1简介
为什么需要?原因很简单,当需要有大量的边去连时,用线段树优化可以直接用点连向区间,或从区间连向点,或从区间连向区间,如果普通连边,复杂度是不可比拟的。下面简单讲解一下线段树(ST)优化建图。
2讲解
2.1 两棵树
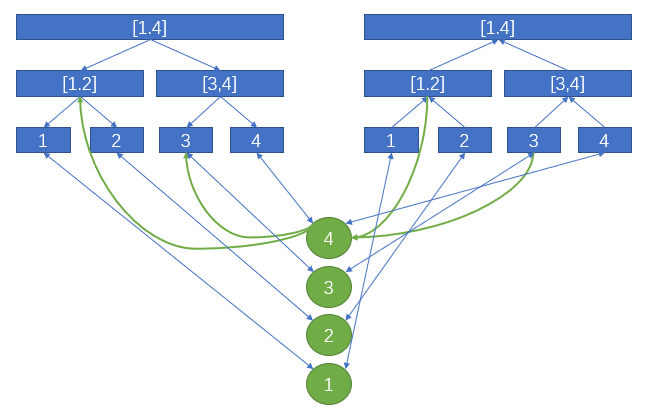
线段树优化建图需要两棵树:入树和出树,入树指被点或区间指向的树,连边时从结点或边连向入树,出树指连向点或结点的边的树,连边时连向点或结点。入树之间的边是父亲指向儿子,出树之间的边是儿子指向父亲,如果结点个数为n,我们通常用k表示第一颗线段树,k+4*n表示第二颗线段树,k+8*n表示普通结点(为什么要有普通结点一会说),这样,实际上给每颗线段树都留了4*n个结点。
.png)
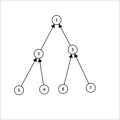
上面的三张图分别是出树,入树和连结点时的样子。
为什么要这么做,可以这么想,出树保证的是所有的儿子结点都能走到他们父亲结点连向的边,
所有的儿子结点都能被两项他们父亲节点的边走到,所以不难理解为什么出树和入树的父亲结点与儿子结点之间的边这样建。
2.2 建树
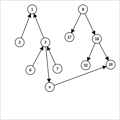
这个过程其实与我们普通线段树的建法一样,只不过多了一个步骤加边,同时,如果当前结点已经是叶子结点,还需要一步操作,及新建一个绿色结点,把每棵树的子结点向对应绿色结点连一条 无向边,如图(蓝色边):
代码:
inline void build(ll k,ll l,ll r){
if(l==r){
add(k,l+8*n,0);add(l+8*n,k,0);
add(k+4*n,l+8*n,0);add(l+8*n,k+4*n,0);
return;
}
add(k,k*2,0);add(k,k*2+1,0);
add(k*2+4*n,k+4*n,0);add(k*2+1+4*n,k+4*n,0);
ll mid=l+r>>1;
build(k*2,l,mid);build(k*2+1,mid+1,r);
}
实际上,我们建绿色结点是为了方便我们连点对区间边,比如上图,同时也给了一个点连到区间的例子。所以,如果没有点对区间的连边,这个过程可以省略。(但是为了好理解,博主一般打上)
2.3 邻接表
这个地方只放代码,不知道的请参考其他博客
struct edge{
ll next,to,w;
inline void intt(ll to_,ll next_,ll w_){
next=next_;to=to_;w=w_;
}
};
edge li[M];ll head[N],tail;
inline void add(ll from,ll to,ll w){
li[++tail].intt(to,head[from],w);
head[from]=tail;
}
2.4 加边
这个地方只讲解点与区间相连,事实上,如果是区间与区间想连的话,可以通过加一个虚拟结点来实现,如下: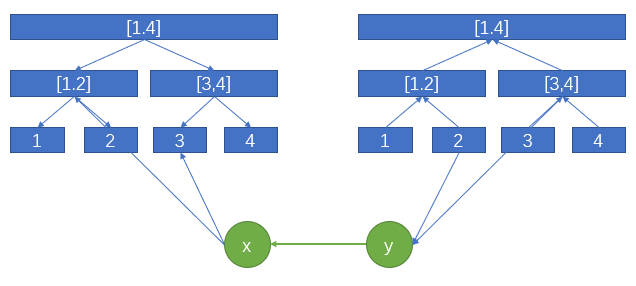
注:虚拟结点之间的边带权值,其余边权值为0。
这里的加边和我们对普通线段树的操作大同小异。只需要注意边的方向就行了:
inline void addh(ll k,ll z,ll y,ll pd,ll u,ll w){
ll l=p[k].l,r=p[k].r,mid=l+r>>1;
if(l==z&&y==r){
if(!pd) return add(u+8*n,k,w);
else return add(k+4*n,u+8*n,w);
}
if(y<=mid) addh(k*2,z,y,pd,u,w);
else if(z>mid) addh(k*2+1,z,y,pd,u,w);
else addh(k*2,z,mid,pd,u,w),addh(k*2+1,mid+1,y,pd,u,w);
}
代码里的pd是用来判断是边连向区间还是从区间连向边。
注:只有线段树上的点连到绿色结点时才带边权,如2.2那个图,只有绿色边带权值。
2.5 跑最短路
事实上可以跑dij,如果是只有0边权和1边权建议跑01bfs,因为01bfs的复杂度是\(O(n)\)
现在放01bfs的代码如下,想看dij代码的可以去本博客存的最短路代码中去看:
deque<ll> q;ll d[N];
bool vis[N];
inline void bfs(ll s){
memset(d,INF,sizeof(d));
q.push_front(s);d[s]=0;
while(q.size()){
ll top=q.front();q.pop_front();
if(vis[top]) continue;
vis[top]=1;
for(ll k=head[top];k;k=li[k].next){
ll to=li[k].to;
if(vis[to]) continue;
if(d[to]>d[top]+li[k].w){
d[to]=d[top]+li[k].w;
if(li[k].w) q.push_back(to);
else q.push_front(to);
}
}
}
}
01bfs的思想其实就是贪心,实现方法双端队列,0边权加到队首,1边权加到队尾,这样从队头取结点能保证它经过了较多的0边。其余与普通bfs无异。
2.6注意事项
- 注意在有点到区间连线时才必须要绿色节点,其余情况绿色节点不必要。
- 在区间与区间连线时我们使用了虚拟节点,事实上直接区间连区间也未尝不可,但是我们习惯上操作还是喜欢用区间连向点,这样只需要写一个函数,方便操作。
- 在题目要求要无向边时(即双向边),出树和入树父亲结点与儿子结点之间边的方向不变,若点连向区间时直接操作即可,例如从区间a到点b,参照2.2的图即可,但是如果是区间连向区间,需要建虚拟结点的话,还是应当多建虚拟节点,不能用原有虚拟节点去连双向边。例如,区间a到区间b连无向边,从a连向b需要建立两个虚拟结点,从b再连向a需要再建立两个虚拟节点,否则,会出现原来题目中没有出现的边,导致最短路出错。切忌!
3例题
3.1 洛谷CF786B
https://www.luogu.com.cn/problem/CF786B
裸题,连完边跑dij即可。具体实现如下:
代码:
#include<iostream>
#include<cstdio>
#include<cmath>
#include<algorithm>
#include<cstring>
#include<sstream>
#include<queue>
#include<map>
#include<vector>
#include<set>
#include<deque>
#include<cstdlib>
#include<ctime>
#define dd double
#define ld long double
#define ll long long
#define ull unsigned long long
#define N 900010
#define M 9000090
using namespace std;
const ll INF=0x3f3f3f3f;
struct edge{
ll to,next,w;
inline void intt(ll to_,ll next_,ll w_){
to=to_;next=next_;w=w_;
}
};
edge li[M];ll head[N],tail;
inline void add(ll from,ll to,ll w){
li[++tail].intt(to,head[from],w);
head[from]=tail;
}
ll n,q,s;
struct rode{
ll l,r;
};
rode p[N];
inline void build(ll k,ll l,ll r){
p[k].l=l;p[k].r=r;
if(l==r){
add(l+8*n,k,0);add(k+4*n,l+8*n,0);
add(k,l+8*n,0);add(l+8*n,k+4*n,0);
return;
}
add(k,k*2,0);add(k*2+n*4,k+n*4,0);
add(k,k*2+1,0);add(k*2+1+n*4,k+n*4,0);
ll mid=l+r>>1;
build(k*2,l,mid);build(k*2+1,mid+1,r);
}
inline void addh(ll k,ll z,ll y,ll pd,ll u,ll w){
ll l=p[k].l,r=p[k].r,mid=l+r>>1;
if(l==z&&y==r){
if(!pd) return add(u+8*n,k,w);
else return add(k+4*n,u+8*n,w);
}
if(y<=mid) addh(k*2,z,y,pd,u,w);
else if(z>mid) addh(k*2+1,z,y,pd,u,w);
else addh(k*2,z,mid,pd,u,w),addh(k*2+1,mid+1,y,pd,u,w);
}
struct DIJ{
ll d[N];bool vis[N];
struct node{
ll to,w;
node() {}
node(ll to,ll w) : to(to),w(w) {}
};
struct cmp{
inline bool operator () (node a,node b){
return a.w>b.w;
}
};
priority_queue<node,vector<node>,cmp> q;
inline void Dij(ll s){
memset(d,INF,sizeof(d)); d[s]=0;
q.push(node(s,0));
while(!q.empty()){
node fr=q.top();q.pop();
if(vis[fr.to]) continue;
vis[fr.to]=1;
for(int k=head[fr.to];k;k=li[k].next){
ll to=li[k].to;
if(!vis[to]&&d[to]>d[fr.to]+li[k].w){
d[to]=d[fr.to]+li[k].w;
q.push(node(to,d[to]));
}
}
}
}
};
DIJ dij;
int main(){
scanf("%lld%lld%lld",&n,&q,&s);
build(1,1,n);
for(ll i=1;i<=q;i++){
ll op,v,u,w,l,r;
scanf("%lld",&op);
if(op==1){
scanf("%lld%lld%lld",&v,&u,&w);
add(v+8*n,u+8*n,w);
}
else if(op==2){
scanf("%lld%lld%lld%lld",&v,&l,&r,&w);
addh(1,l,r,0,v,w);
}
else if(op==3){
scanf("%lld%lld%lld%lld",&v,&l,&r,&w);
addh(1,l,r,1,v,w);
}
}
s+=8*n;
dij.Dij(s);
for(int i=1;i<=n;i++){
printf("%lld ",dij.d[i+8*n]<=4e18?dij.d[i+8*n]:-1);
}
return 0;
}
3.2 洛谷P6348
是区间连向区间的例题,注意虚拟节点不能乱用即可,虚拟节点的编号为k+9*n。
#include<iostream>
#include<cstdio>
#include<cmath>
#include<algorithm>
#include<cstring>
#include<sstream>
#include<queue>
#include<map>
#include<vector>
#include<set>
#include<deque>
#include<cstdlib>
#include<ctime>
#define ld long double
#define ll long long
#define ull unsigned long long
#define N 9000100
#define M 10001000
using namespace std;
const ll INF=0x3f3f3f3f;
struct edge{
ll next,to,w;
inline void intt(ll to_,ll next_,ll w_){
next=next_;to=to_;w=w_;
}
};
edge li[M];ll head[N],tail;
inline void add(ll from,ll to,ll w){
li[++tail].intt(to,head[from],w);
head[from]=tail;
}
ll p[N],n,m,s;
inline void build(ll k,ll l,ll r){
if(l==r){
add(k,l+8*n,0);add(l+8*n,k,0);
add(k+4*n,l+8*n,0);add(l+8*n,k+4*n,0);
return;
}
add(k,k*2,0);add(k,k*2+1,0);
add(k*2+4*n,k+4*n,0);add(k*2+1+4*n,k+4*n,0);
ll mid=l+r>>1;
build(k*2,l,mid);build(k*2+1,mid+1,r);
}
inline void addh(ll k,ll l,ll r,ll z,ll y,ll pd,ll u,ll w){
if(l==z&&r==y){
if(!pd) return add(u,k,w);
else return add(k+4*n,u,w);
}
ll mid=l+r>>1;
if(y<=mid) addh(k*2,l,mid,z,y,pd,u,w);
else if(z>mid) addh(k*2+1,mid+1,r,z,y,pd,u,w);
else addh(k*2,l,mid,z,mid,pd,u,w),addh(k*2+1,mid+1,r,mid+1,y,pd,u,w);
}
deque<ll> q;ll d[N];
bool vis[N];
inline void dfs(ll s){
memset(d,INF,sizeof(d));
q.push_front(s);d[s]=0;
while(q.size()){
ll top=q.front();q.pop_front();
if(vis[top]) continue;
vis[top]=1;
for(ll k=head[top];k;k=li[k].next){
ll to=li[k].to;
if(vis[to]) continue;
if(d[to]>d[top]+li[k].w){
d[to]=d[top]+li[k].w;
if(li[k].w) q.push_back(to);
else q.push_front(to);
}
}
}
}
int main(){
scanf("%lld%lld%lld",&n,&m,&s);
build(1,1,n);
ll tailx=9*n;
for(ll i=1;i<=m;i++){
ll a,b,c,dd;
scanf("%lld%lld%lld%lld",&a,&b,&c,&dd);
addh(1,1,n,a,b,1,++tailx,0);
addh(1,1,n,c,dd,0,++tailx,0);
add(tailx-1,tailx,1);
addh(1,1,n,c,dd,1,++tailx,0);
addh(1,1,n,a,b,0,++tailx,0);
add(tailx-1,tailx,1);
}
dfs(s+8*n);
for(ll i=1;i<=n;i++) printf("%lld\n",d[i+8*n]);
return 0;
}
这里在附上引用中大佬的代码,他的代码中没有绿色节点。
int n,m,s,id[N],cnt;
struct Node {int l,r;}t[N];
void build(int p,int l,int r) {
t[p].l=l, t[p].r=r;
if(l==r) {
id[l]=p;
return;
}
add(p,p*2,0), add(p*2+n*4,p+n*4,0);
add(p,p*2+1,0), add(p*2+1+n*4,p+n*4,0);
build(p*2,l,(l+r)/2), build(p*2+1,(l+r)/2+1,r);
}
void adds(int p,int x,int y,bool type,int u) {
int l=t[p].l, r=t[p].r, mid=((l+r)>>1);
if(l==x&&y==r) {
if(!type) return add(u,p,0);
else return add(p+4*n,u,0);
}
if(y<=mid) adds(p*2,x,y,type,u);
else if(x>mid) adds(p*2+1,x,y,type,u);
else adds(p*2,x,mid,type,u), adds(p*2+1,mid+1,y,type,u);
}
int d[N];
void bfs() {
deque<int>q; q.push_front(s);
memset(d,0x3f,sizeof(d)); d[s]=0;
while(!q.empty()) {
int u=q.front(); q.pop_front();
for(int i=hd[u],v;i;i=e[i].nxt)
if(d[v=e[i].to]>d[u]+e[i].w) {
d[v]=d[u]+e[i].w;
if(!e[i].w) q.push_front(v);
else q.push_back(v);
}
}
}
signed main() {
scanf("%d%d%d",&n,&m,&s);
build(1,1,n);
cnt=8*n;
for(int i=1,a,b,c,dd;i<=m;i++) {
scanf("%d%d%d%d",&a,&b,&c,&dd);
int x=++cnt, y=++cnt;
add(y,x,1), adds(1,c,dd,0,x), adds(1,a,b,1,y);
x=++cnt, y=++cnt;
add(y,x,1), adds(1,a,b,0,x), adds(1,c,dd,1,y);
}
for(int i=1;i<=n;i++) add(id[i],id[i]+4*n,0), add(id[i]+4*n,id[i],0);
s=id[s]+4*n;
bfs();
for(int i=1;i<=n;i++) printf("%d\n",d[id[i]]);
return 0;
}
引用:
https://www.luogu.com.cn/blog/forever-captain/DS-optimize-graph