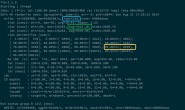
C语言求1000以内的所有素数
老外的代码,写的还是很严谨的。
/*
This is a simple program which calculates all prime numbers up to
1000. This is not the most efficient algorithm, but it is easy
to follow. I'll post some more efficient algorithms soon that
avoid redundancy, but the goal of this code snippet is a semi-brute
force method that is easy to understand.
The general approach is to declare everything prime, then start crossing
off multiples of prime numbers from the prime number list.
I do make use of two facts to make the program not completely brute-force.
One, the outer loop only goes up to the square root of N. Any non-prime
number will have a factor less than or equal to its square root.
Two, any multiple of a non-prime number is also a multiple of a smaller
prime number, so any multiple of a non-prime number has already been
flagged as non-prime. Thus there is no need to flag multiples of numbers
that are non-prime, so the inner for-loop can be short-circuited.
There are some other mathematical rules that can improve efficiency of the
inner and outer for-loops, but I'll stick with just these two for now for
easier understanding.
*/
#include <iostream>
#include <cmath>
using namespace std;
int main ()
{
const int N = 1000;
const int SQR_ROOT_N = (int) (sqrt ((double) N));
bool prime[N + 1];
prime[0] = false; // 0 is not prime
prime[1] = false; // 1 is not prime
for (int i = 2; i <= N; i++)
prime[i] = true; // flag all numbers as prime initially
for (int i = 2; i <= SQR_ROOT_N; i++)
{
if (prime[i]) // no need for inner loop if i is not prime
{
for (int j = 2 * i; j <= N; j+=i)
prime[j] = false; // j is a multiple of i, thus not prime.
}
}
// display prime numbers
cout << "Here are the prime numbers\n\n";
for (int i = 2; i <= N; i++)
{
if (prime[i])
cout << i << endl;
}
return 0;
}