C语言之数据在内存中的存储
在我们学习此之前,我们先来回忆一下C语言中都有哪些数据类型呢?
首先我们来看看C语言中的基本的内置类型:
char //字符数据类型 short //短整型 int //整形 long //长整型 long long //更长的整形 float //单精度浮点数 double //双精度浮点数
在这,值得一提的是C语言的基本类型中并没有字符串类型,而字符串的实现一般都是通过数组来实现
C语言的数据类型我们可以基本分为5种类型
1.整型家族
char //字符形其实也属于整形,因为在字符的储存是存的是它的ASCII码值 unsigned char signed char
short unsigned short [int] signed short [int]
int unsigned int signed int
long unsigned long [int] signed long [int]
2.浮点型家族
float double
3.构造类型
> 数组类型 > 结构体类型 struct > 枚举类型 enum > 联合类型 union
4.指针类型
int *pi;
char *pc;
float* pf;
void* pv;
5.空类型
void 表示空类型(无类型) 通常应用于函数的返回类型、函数的参数、指针类型。
在复习了一遍数据类型之后,我们现在来谈谈数据到底是怎么存储的
一.整形在内存中的存储
首先我们来看看整形
比如,下面再平常不过的式子
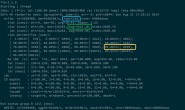
int a = 10; int b = -20;
先不管其他的,我们先来看看它在内存里是怎么放的
我们得到了一串数字,而这些数字代表这什么呢?
原来是一串16进制的数字啊
我们知道一个整形系统分配四个字节来储存
而一个字节又有8个比特位,所以就会有32个二进制的0或1.我们把上面两串16进制的数字转为2进制来看一看有什么不同。
00001010000000000000000000000000 11101100111111111111111111111111
在这我们来看看10的二进制
00000000000000000000000000001010
有什么不同呢?
在这我们来介绍一下原码,反码,补码
计算机中的有符号数有三种表示方法,即原码、反码和补码。
三种表示方法均有符号位和数值位两部分,符号位都是用0表示“正”,用1表示“负”,而数值位 三种表示方法各不相同。
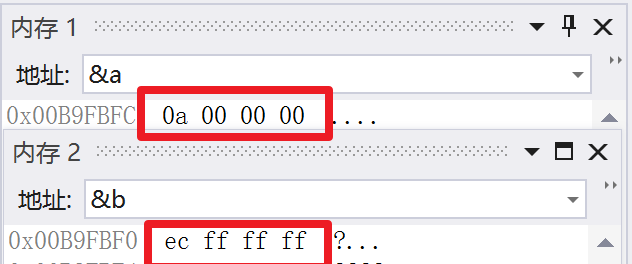
原码
直接将二进制按照正负数的形式翻译成二进制就可以。
反码
将原码的符号位不变,其他位依次按位取反就可以得到了。
补码
反码+1就得到补码。
那我们来举个例子
对于正整数,它的原码 反码 补码 都相同
那么对于负整数呢,继续来看看

现在我们应该对原码反码补码有了初步的了解,我们继续接着上面来看
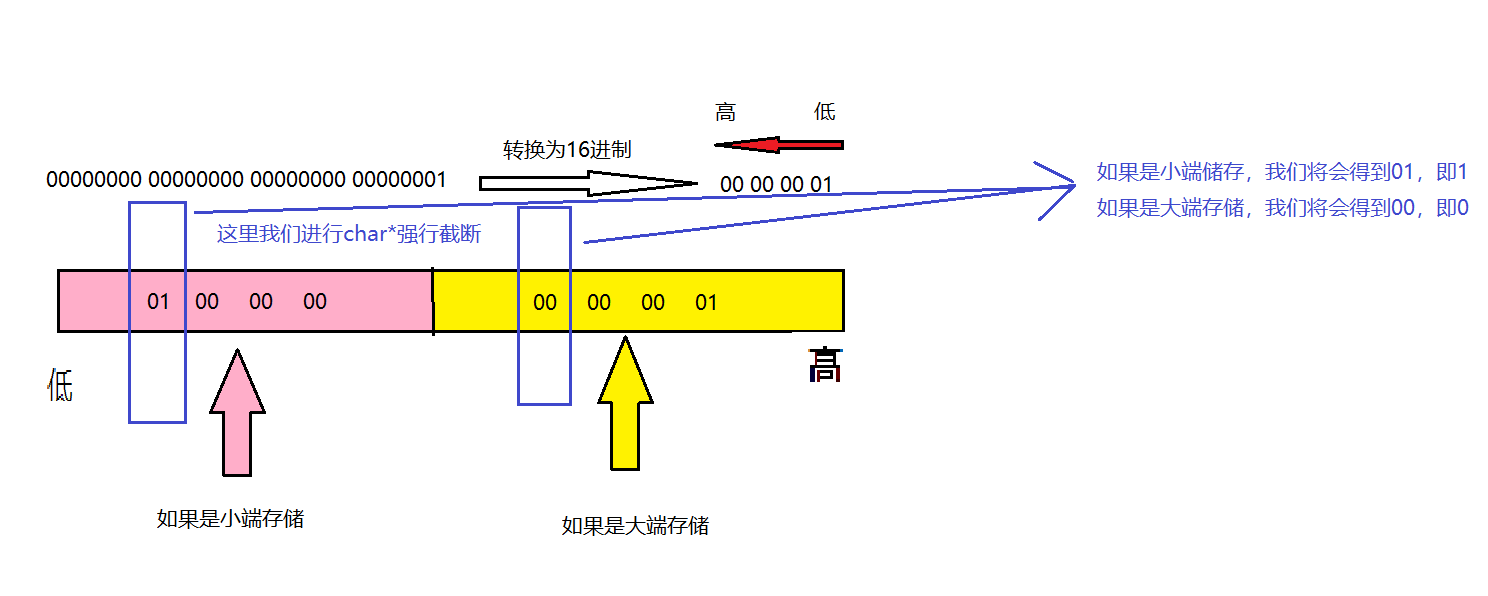
计算机储存的是补码,那么我们现在来写出 10 和 -20 的补码来看看于上述内存中存的是否一样
// 10的原码,反码,补码 // 00000000000000000000000000001010 // -20的原码 // 10000000000000000000000000010100 // -20的反码 // 11111111111111111111111111101011 // -20的补码 // 11111111111111111111111111101100
我们将其转换为16进制来看看
10的补码 00 00 00 0A -20的补码 FF FF FF EC
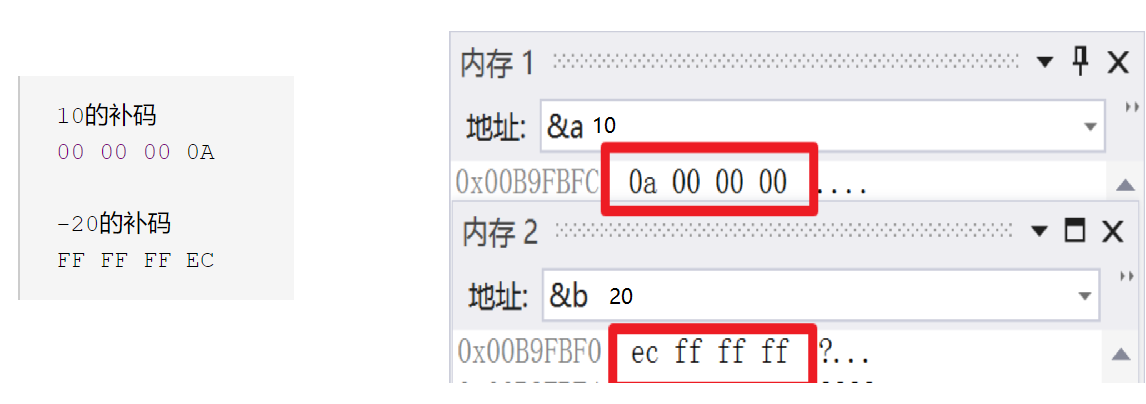
这时,我们似乎发现它们俩的补码似乎按字节反了过来,这是为什么呢?
所以,这又引出了一个新的知识点——大小端
介绍 什么大端小端: 大端(存储)模式,是指数据的低位保存在内存的高地址中,而数据的高位,保存在内存的低地址中;
小端(存储)模式,是指数据的低位保存在内存的低地址中,而数据的高位,,保存在内存的高地址中。 为什么有大端和小端: 为什么会有大小端模式之分呢?这是因为在计算机系统中,我们是以字节为单位的,
每个地址单元都对应着一 个字节,一个字节为8bit。但是在C语言中除了8bit的char之外,还有16bit的short型,32bit的long型(要看具 体的编译器),
另外,对于位数大于8位的处理器,例如16位或者32位的处理器,由于寄存器宽度大于一个字 节,那么必然存在着一个如果将多个字节安排的问题。
因此就导致了大端存储模式和小端存储模式。 例如一个 16bit 的 short 型 x ,在内存中的地址为 0x0010 , x 的值为 0x1122 ,
那么 0x11 为高字节, 0x22 为低字节。
对于大端模式,就将 0x11 放在低地址中,即 0x0010 中, 0x22 放在高地址中,即 0x0011 中。
小端模式,刚好相反。
我们常用的 X86 结构是小端模式,而 KEIL C51 则为大端模式。很多的ARM,DSP都为小端模式。有些ARM处理器还可以由硬件来选择是大端模式还是小端模式。
那么怎么来判断自己的编译器是大端还是小端呢?
#define _CRT_SECURE_NO_WARNINGS 1 #include<stdio.h> int check_sys() { int a = 1; return (*(char*)&a); } int main() { int ret = check_sys(); if (ret == 1) { printf("小端\n"); } else { printf("大端\n"); } return 0; }
运行结果如下

但,我们可能还是不知道它是怎么实现的,所以在这解释一下
相信现在大家应该对此清楚了不少
那么,现在我们将上述代码微做修改用我们的Keil C51来试一试
#include <reg52.h> #define uint unsigned int sbit LSA=P2^2; sbit LSB=P2^3; sbit LSC=P2^4; void delay(uint a) { while(a--); } int check_sys() { int a = 1; return (*(char*)&a); } int main() { int ret = check_sys(); LSA=1; LSB=1; LSC=1; while(1) { if (ret == 1) { P0=0x06;//在数码管的首位显示 1 } else { P0=0x3f;//在数码管的首位显示 0 } delay(1000); } }
运行结果
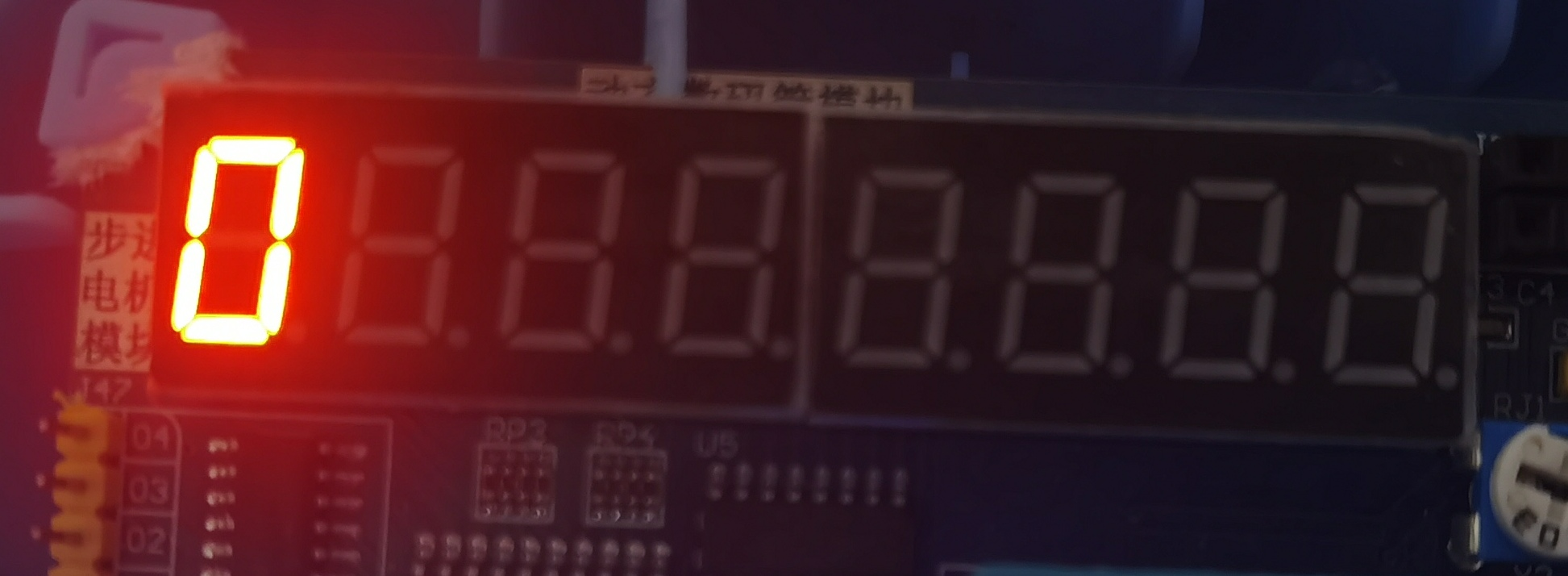
结果正如介绍所说,keil c51为大端存储
那么接下来我们来看看几道题,以此加深我们对此的理解
1. //输出什么? #include <stdio.h> int main() { char a= -1; signed char b=-1;
unsigned char c=-1; printf("a=%d,b=%d,c=%d",a,b,c);
return 0; }
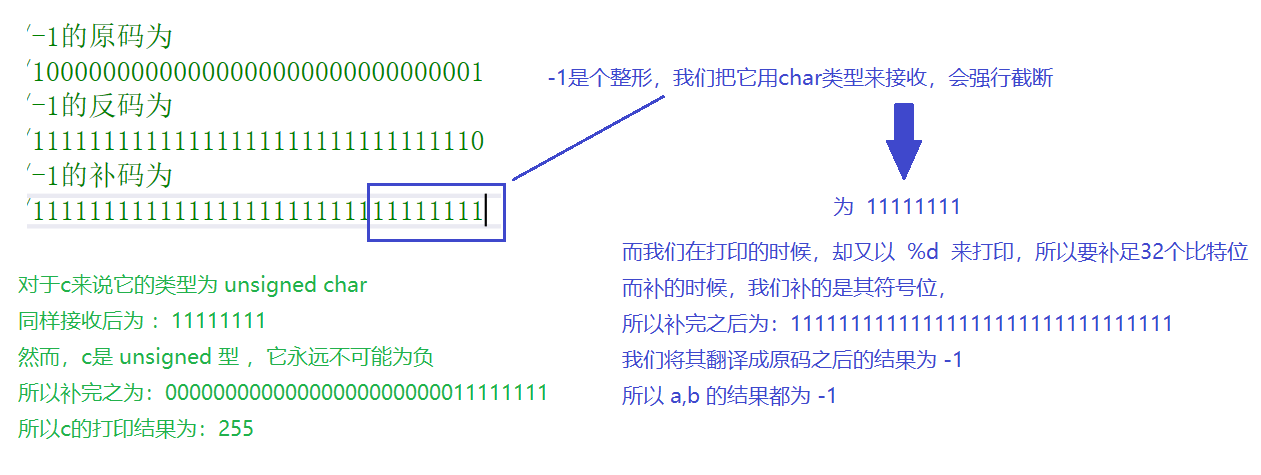
运行结果:
2. #include <stdio.h> unsigned char i = 0;
int main() { for(i = 0;i<=255;i++) { printf("hello world\n"); } return 0; }
那,这一题的结果 不知大家是否能够想到是一直打印 hello world

我们对整形的存储就停在这
接下来我们以一道题来进入浮点型在内存中的存储
int main() { int n = 9; float *pFloat = (float *)&n;
printf("n的值为:%d\n",n);
printf("*pFloat的值为:%f\n",*pFloat);
*pFloat = 9.0;
printf("n的值为:%d\n",n);
printf("*pFloat的值为:%f\n",*pFloat);
return 0; }
这道题许多人会给出 9 9.000000 9 9.000000 的答案
可事实并非如此
这题的答案为:

为什么呢?
所以
二.浮点型在内存中的存储
根据国际标准IEEE(电气和电子工程协会)754,任意一个二进制浮点数V可以表示成下面的形式:
(-1)^S * M * 2^E
(-1)^s表示符号位,当s=0,V为正数;当s=1,V为负数。
M表示有效数字,大于等于1,小于2。
2^E表示指数位。
我们举个例子如 5.5
我们可以写成 101.1(2进制)
按上述改为:
(-1)^ 0 *1.011*2^2
那么 S=0, M=1.011, E=2.
IEEE 754规定: 对于32位的浮点数,最高的1位是符号位s,接着的8位是指数E,剩下的23位为有效数字M。

对于64位的浮点数,最高的1位是符号位S,接着的11位是指数E,剩下的52位为有效数字M。

而 IEEE 754对有效数字M和指数E,还有一些特别规定。 前面说过, 1≤M<2 ,也就是说,M可以写成 1.xxxxxx 的形 式,其中xxxxxx表示小数部分。
IEEE 754规定,在计算机内部保存M时,默认这个数的第一位总是1,因此可以被舍去,只保存后面的xxxxxx部分。 比如保存1.01的时候,只保存01,等到读取的时候,再把第一位的1加上去。这样做的目的,是节省1位有效数字。 以32位浮点数为例,留给M只有23位,将第一位的1舍去以后,等于可以保存24位有效数字。
至于指数E,情况就比较复杂
首先,E为一个无符号整数(unsigned int) 这意味着,如果E为8位,它的取值范围为0~255;如果E为11位,它的 取值范围为0~2047。但是,我们知道,科学计数法中的E是可以出现负数的,所以IEEE 754规定,存入内存时E的真 实值必须再加上一个中间数,对于8位的E,这个中间数是127;对于11位的E,这个中间数是1023。比如,2^10的E 是10,所以保存成32位浮点数时,必须保存成10+127=137,即10001001。
那么根据上面所述 现在 S=0, M=011, E=129
所以在内存中就为 0 10000001 01100000000000000000000 将其换为16进制为 40 b0 00 00
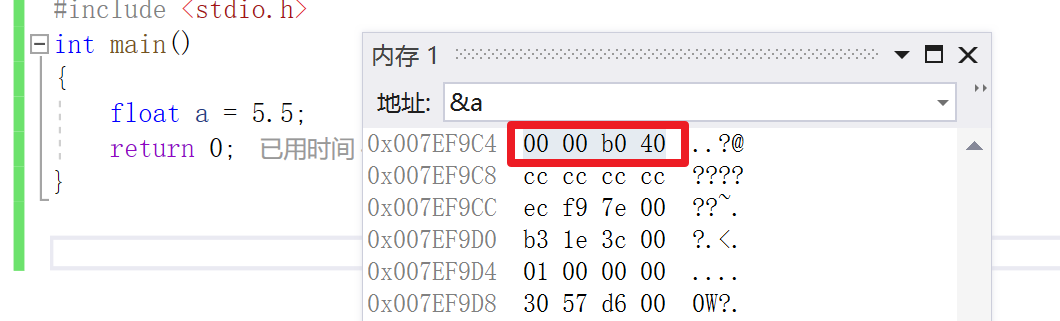
然后,指数E从内存中取出还可以再分成三种情况:
1.E不全为0或1
这时,浮点数就采用下面的规则表示,即指数E的计算值减去127(或1023),得到真实值,再将有效数字M前 加上第一位的1。
2.E全为0
这时,浮点数的指数E等于1-127(或者1-1023)即为真实值, 有效数字M不再加上第一位的1,而是还原为
0.xxxxxx的小数。这样做是为了表示±0,以及接近于0的很小的数字。
3.E全为1
这时,如果有效数字M全为0,表示±无穷大(正负取决于符号位s);
此时是否对前面所提到的那一题恍然大悟了呢