在机器学习中，我们一直期望学习一个泛化能力（generalization）强的函数只有泛化能力强的模型才能很好地适用于整个样本空间，才能在新的样本点上表现良好。

机器学习基础——规则化（Regularization）

\[y=a+bx+cx^2+dx^3\tag{1} \]

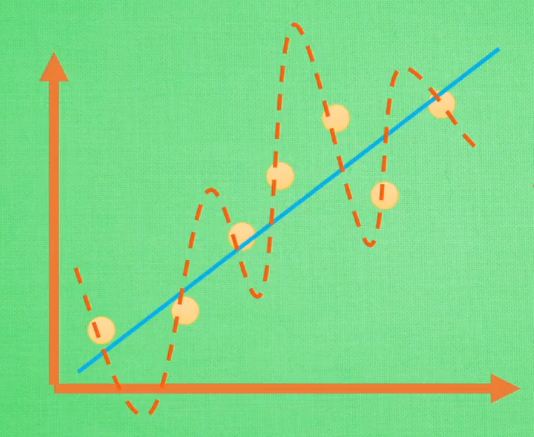
如上图，公式(1)完美地拟合了训练空间中所有的点，如果具备过拟合（overfiting）的能力，那么这个方程肯定是一个比较复杂的非线性函数。正是因为这里的 $x^2$ 和 $x^3$ 的参数 $c$ 和 $d$ 使得这条曲线可以弯来弯去去拟合训练样本空间中的点。但是我们希望的是模型可以学习到图面中这条蓝色的曲线，因为它能更有效地概括数据，所以我们希望 $c$ 和 $d$ 的值相对减小。虽然蓝色函数训练时对应的误差要比红色的大，但它概括起数据来要比蓝色的好。

训练集通常只是整个样本空间很小的一部分，在训练机器学习模型时，稍有不注意，就可能将训练集中样本的特性当作全体样本的共性，以偏概全，而造成过拟合，如何避免过拟合，是机器学习模型时亟待解决的绊脚石。

从问题的根源出发，解决过拟合无非两种途径：

使训练集能够尽可能全面的描述整个样本空间。因此又存在两种解决方案。①减少特征维数，特征维数减少了，样本空间的大小也随之减少了，现有数据集对样本空间的描述也就提高了。②增加训练样本数量，试图直接提升对样本空间的描述能力。
加入规则化项。（规则化在有些文档中也称作正规化）

第一种方法的人力成本通常很大，所以在实际中，我们通常采用第二种方法提升模型的泛化能力。

规则化（Regularization）

首先回顾一下，在寻找模型最优参数时，我们通常对损失函数采用梯度下降（gradient descent）算法

\[w^*,b^*=arg \ {min_{w,b}}\sum^m_{i=1} (y^{(i)}-(w^Tx^{(i)}+b))^2\tag{2} \]

\[\frac{∂L}{∂w}=\sum^m_{i=1}2(y^{(i)}-(w^Tx^{(i)}+b))(-x^{(i)})\tag{3} \]

\[\frac{∂L}{∂b}=\sum^m_{i=1}2(y^{(i)}-(w^Tx^{(i)}+b))(-1)\tag{3} \]

通过上述公式，我们将一步步走到损失函数的最低点（不考虑局部最小值和鞍点的情况），这是的 $w$ 和 $b$ 就是我们要找的最优参数。

我们可以看到，当我i们的损失函数只考虑最小化训练误差，希望找到的最优函数能够尽可能的拟合训练数据。但是正如我们所了解的，训练集不能代表整个样本空间，所以训练误差也不能代表测试误差，训练误差只是经验风险，我们不能过分依赖这个值。当我们的函数对训练集拟合特别好，训练误差特别小时，我们也就走进了一个极端——过拟合。

为了解决这个问题，研究人员提出了规则化（regularization）方法。通过给模型参数附加一些规则，也就是约束，防止模型过分拟合训练数据。规则化通过在原有损失函数的基础上加入规则化项实现。

此时，最优化的目标函数如下：

\[w^*=argmin_w[\sum_iL(y^{(i)},f(x^{(i)};w))+λΩ(w)]\tag{4} \]

其中，第一项对应于模型在训练集上的误差，第二项对应于规则化项。为了使得该目标函数最小，我们需要对训练误差和规则化项之间做出权衡。

那应该选择怎样的表达式作为规则化项呢？以下引用李航博士《统计学习方法》中的一些描述：

规则化是结构风险最小化策略的实现，是在经验风险最小化上加一个规则化项（regularizer）或惩罚项（penalty term）。规则化项一般是模型复杂度的单调递增函数，模型越复杂，规则化值就越大。比如，规则化项可以是模型参数向量的范数。

规则化符合奥卡姆剃刀（Occam‘s razor）原理。奥卡姆剃刀原理应用于模型选择时变为以下想法：在所有可能选择的模型中，能够很好地解释已知数据并且十分简单才是最好的模型，也就是应该选择的模型。从贝叶斯估计的角度来看，规则化项对应于模型的先验概率。可以假设复杂的模型有较大的先验概率，简单的模型有较小的先验概率。

我们通常采用L1-范数和L2-范数作为规则化项。

L-1范数

向量的L1-范数是向量的元素绝对值之和，即

\[||x||_1=\sum_i(x_i)\tag{5} \]

当采用L1-范数作为规则化项对参数进行约束时，我们的优化问题就可以写成一下形式：

\[min_w \frac{1}{2}(y-Xw)^2\\ s.t. \quad ||w||_1\leq C \]

采用拉格朗日乘子法可以将约束条件合并到最优化函数中，即

\[min_w \frac{1}{2}(y-Xw)^2+λ||w|| _1 \]

其中，$λ$ 是与 $C$ 一一对应的常数，用来权衡误差项和规则化项，$λ$ 越大，约束越强。二维情况下分别将损失函数的等高线图和L1-范数规则化约束画在同一个坐标轴下，

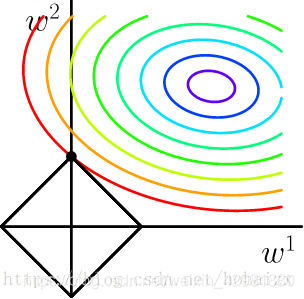L1-范数约束对应于平面上一个正方形norm ball。不难看出，等高线与norm ball首次相交的地方可以使整个目标函数最小，即最优解。可以看到，L1-ball在和每个坐标轴相交的地方都有一个“角”出现，大部分时候等高线都会与norm ball在角的地方相交。这样部分参数值被置为0，相当于该参数对应的特征将不再发挥作用，实现了特征选择，增加了模型的可解释性。关于L1-范数规则化，可以解释如下：训练出来的参数代表权重，反映了特征的重要程度，比如 $y=20x_1+5x_2+3$ 中特征 $x_1$ 明显比 $x_2$ 更重要，因为 $x_1$ 的变动相较于 $x_2$ 的变动会给 $y$ 带来更大的变化。在人工选取的特征中，往往会存在一些冗余特征或者无用特征，L1-范数规则化将这些特征的权重置为0，实现了特征选择，同样也简化了模型。

L1-范数在 $x=0$ 处存在拐点，所以不能直接求得解析解，需要用次梯度方法处理不可导的凸函数。

L2-范数

除了L1-范数，还有一种广泛使用的规则化范数：L2-范数。向量的L2-范数是向量的模长，即

\[||x||_2=\sqrt{\sum_i(x_i^2)}\tag{6} \]

当采用L2-范数作为规则化项对参数进行约束时，我们的优化问题可以写成以下形式：

\[min_w \frac{1}{2}(y-Xw)^2 \\ s.t. \quad ||w||_2 \leq C \]

同样可以将约束条件合并到最优化函数中，得到如下函数

\[min_w \frac{1}{2}(y-Xw)^2+λ||w|| _2 \]

也将损失函数的等高线图和L2-范数规则化约束画在同一坐标轴下，

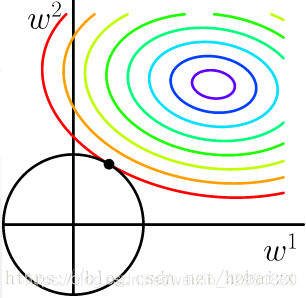L2-范数约束对应于平面上一个圆形norm ball。等高线与norm ball首次相交的地方就是最优解。与L1-范数不同，L2-范数使得每一个 $w$ 都很小，都接近于0，但不会等于0，L2-范数规则化仍然试图使用每一维特征。对于L2-范数规则化可以解释如下：L2-范数规则化项将参数限制在一个较小的范围，参数越小，曲面越光滑，因而不会出现很小区间内，弯度很大的情。当 $x$ 出现一个较大的变化时， $y$ 也只会变化一点点，模型因此更加稳定，也就更加generalization。

加入L2-范数规则化项后，目标函数扩展为如下形式： $$ w^*,b^*=arg\ min_{w,b}\sum_{i=1}^m(y^{(i)}-(w^Tx^{(i)}+b)^2 + λ\sum^n_{j=1}w^2_j\tag{7} $$ $$ \frac{∂L}{∂w}=\sum^m_{i=1}2[(y^{(i)}-(w^Tx^{(i)}+b)(-x^{(i)})+λw]\tag{8} $$ $$ \frac{∂L}{∂b}=\sum^m_{i=1}2[(y^{(i)}-(w^Tx^{(i)}+b)(-x^{(i)})(-1)λw]\tag{9} $$

L1-范数和L2-范数的比较

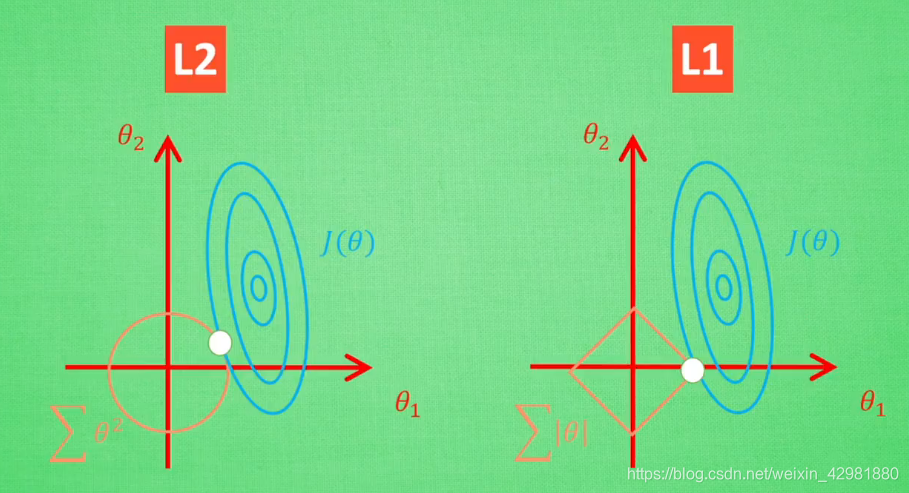假设现在之后两个参数 $θ_1$ 和 $θ_2$ 要学。如图，其中蓝色圆心是误差最小的地方，每条蓝线上的误差都是一样，正规化的方程就是在黄线上产生的额外误差，黄线上的额外误差的值也都一样，所以在黄线和蓝线交点的位置能够使两个误差的和最小，这也是 $θ_1$ 和 $θ_2$ 规则化后的解。

值得一提的是，使用L1-范数的方法很有可能只有 $θ_1$ 的特征被保留，所以很多人采用L1-范数规则化提取对结果`贡献最大`的特征。

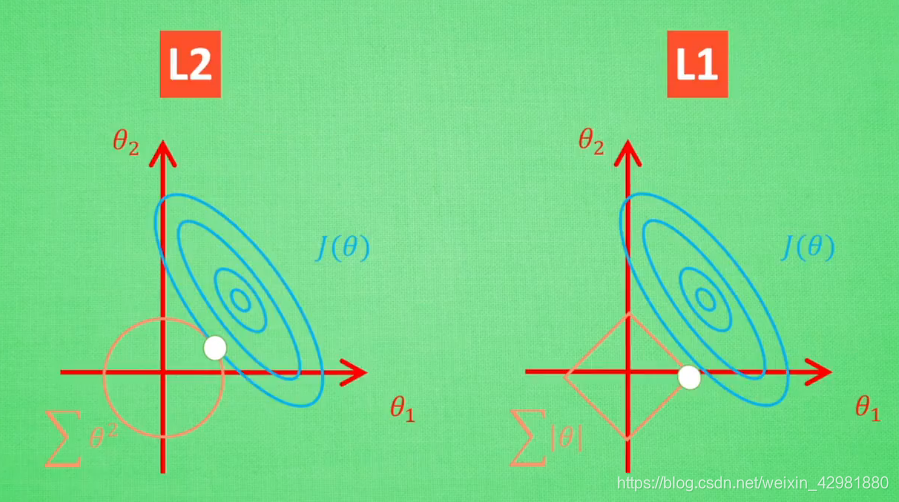
但是L1的解并不是很稳定，比如批数据训练，每一次批数据都会有稍稍不同的误差曲线。L2对于这种变化，交点的移动并不会特别明显，而L1的交点的很可能会跳到很多不同的地方，如下图。因为这些地方的总误差都差不多，侧面说明了L1的解不稳定。