CMU数据库(15-445)-实验2-B+树索引实现(中）删除

3. Delete 实现

附上实验2的第一部分 https://www.cnblogs.com/JayL-zxl/p/14324297.html
附上实验2的第三部分 https://www.cnblogs.com/JayL-zxl/p/14332249.html

1. 删除算法原理

cmu这里给了演示网站 https://www.cs.usfca.edu/~galles/visualization/BPlusTree.html

关于整个删除算法的讲解这个ppthttp://courses.cms.caltech.edu/cs122/lectures-wi2018/CS122Lec11.pdf讲的比较清楚

算法描述见下表

以及下图

2 删除算法实现

2.1 第一步 : 找到包含目标key的leaf node进行删除

1. 找到包含目标key的leaf node

2. 如果当前是空树则立即返回

3. 否则先找到要删除的key所在的page

4. 随后调用RemoveAndDeleteRecord在叶page上直接删除key值

INDEX_TEMPLATE_ARGUMENTS
void BPLUSTREE_TYPE::Remove(const KeyType &key, Transaction *transaction) {
  {
    // 这个专门针对于非并发的delete
    Page *page = FindLeafPage(key, false);
    LeafPage *leafPage = reinterpret_cast<LeafPage*>(page->GetData()); //pined leafPage

    leafPage->RemoveAndDeleteRecord(key,comparator_);

1. RemoveAndDeleteRecord函数

2. 这里实现越来越像Leveldb是怎么回事。。

3. 利用KeyIndex函数实现真的简单。

INDEX_TEMPLATE_ARGUMENTS
int B_PLUS_TREE_LEAF_PAGE_TYPE::RemoveAndDeleteRecord(const KeyType &key, const KeyComparator &comparator) {
  int pos = KeyIndex(key, comparator);
  if (pos < GetSize() && comparator(array_[pos].first, key) == 0) {
    for (int j = pos + 1; j < GetSize(); j++) {
      array_[j - 1] = array_[j];
    }
    IncreaseSize(-1);
  }
  return GetSize();
}

之后就是对于删除的处理，主要有两个一个是合并，一个就是redistribute。具体流程见下

2.2 Coalesce实现流程

叶子结点内关键字个数小于最小值向下执行。调用删除的核心函数CoalesceAndRedistribute

下面是CoalesceAndRedistribute的逻辑

1.如果当前结点是根节点则调用AdjustRoot(node)

这里的提示给了其实这个函数就针对两种情况

• Case1 : old_root_node是内部结点，且大小为1，表示内部结点其实已经没有key了。所以要把它的孩子更新成新的根节点
• Case2 : old_root_node是叶子结点。且大小为0，直接删了就好。

否则不需要有page被删除，则直接return flase

INDEX_TEMPLATE_ARGUMENTS
bool BPLUSTREE_TYPE::AdjustRoot(BPlusTreePage *old_root_node) {
  // case 1 old_root_node (internal node) has only one size
  if (!old_root_node->IsLeafPage() && old_root_node->GetSize() == 1) {
    InternalPage *old_root_page = reinterpret_cast<InternalPage *>(old_root_node);
    page_id_t new_root_page_id = old_root_page->adjustRootForInternal();
    root_page_id_ = new_root_page_id;
    UpdateRootPageId(0);

    Page *new_root_page = buffer_pool_manager_->FetchPage(new_root_page_id);
    BPlusTreePage *new_root = reinterpret_cast<BPlusTreePage *>(new_root_page->GetData());
    new_root->SetParentPageId(INVALID_PAGE_ID);
    buffer_pool_manager_->UnpinPage(new_root_page_id, true);

    return true;
  }
  // case 2 : all elements deleted from the B+ tree
  if (old_root_node->IsLeafPage() && old_root_node->GetSize() == 0) {
    root_page_id_ = INVALID_PAGE_ID;
    UpdateRootPageId(0);
    return true;
  }
  return false;
}

2.否则先判断是否要进行Coalesce

这里要找兄弟结点进行合并，如果满足合并要求的话

1. 判断是否满足合并要求

这里利用一个辅助函数进行判断。如果不超过最大size就可以合并

INDEX_TEMPLATE_ARGUMENTS
template <typename N>
bool BPLUSTREE_TYPE::IsCoalesce(N *nodeL, N *nodeR) {
  // maxSize consider InternalPage and LeafPage
  return nodeL->GetSize() + nodeR->GetSize() <= maxSize(nodeL);
}

️ 合并函数是和直接前驱进行合并，也就是和它左边的node进行合并

2. 判断左边的page是否能进行合并

  // firstly find from left
    if (left_sib_index >= 0) {
      page_id_t sibling_pid = parent->ValueAt(left_sib_index);
      Page *sibling_page = buffer_pool_manager_->FetchPage(sibling_pid);  // pined sibling_page
      N *sib_node = reinterpret_cast<N *>(sibling_page->GetData());
      if (IsCoalesce(node, sib_node)) {
        // coalesce
        // unpin node and deleted node
        bool del_parent = Coalesce(&sib_node, &node, &parent, cur_index, transaction);
         // unpin sibling page
        buffer_pool_manager_->UnpinPage(sibling_pid, true);     
        // unpin parent page;
        buffer_pool_manager_->UnpinPage(parent_pid, true);                             
        if (del_parent) {
          buffer_pool_manager_->DeletePage(parent_pid);
        }
        return false;  // node is merged into sib, and already deleted
      }
      buffer_pool_manager_->UnpinPage(sibling_pid, false);  // unpin sibling page
    }

3. 否则判断右边是否能进行合并

// secondly find from right

    if (right_sib_index < parent->GetSize()) {
      page_id_t sibling_pid = parent->ValueAt(right_sib_index);
      Page *sibling_page = buffer_pool_manager_->FetchPage(sibling_pid);  // pined sibling_page
      N *sib_node = reinterpret_cast<N *>(sibling_page->GetData());
      if (IsCoalesce(node, sib_node)) {
        // coalesce
        // unpin right sib and deleted right sib
        bool del_parent =
            Coalesce(&node, &sib_node, &parent, cur_index, transaction);  
        buffer_pool_manager_->UnpinPage(node->GetPageId(), true);         // unpin sibling page
        buffer_pool_manager_->UnpinPage(parent_pid, true);                // unpin parent page;
        if (del_parent) {
          buffer_pool_manager_->DeletePage(parent_pid);
        }
        return false;  // node is merged into sib, and already deleted
      }
      buffer_pool_manager_->UnpinPage(sibling_pid, false);  // unpin sibling page
    }

4. Coalece函数的实现

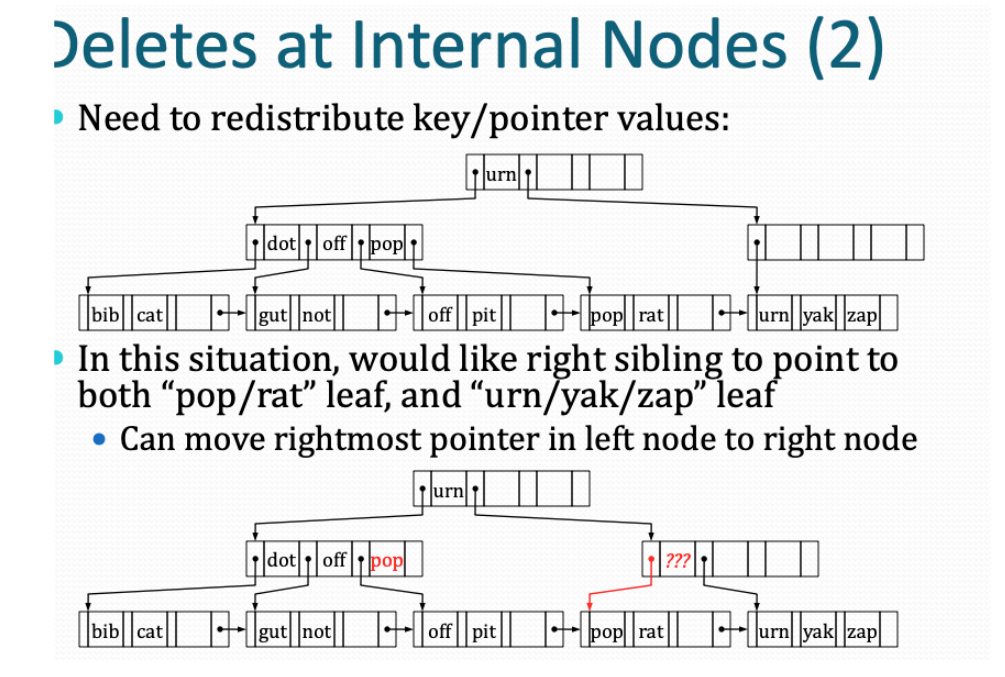
实现之前先看两张图

在合并之后，父亲结点必须要更新。因为移动操作导致了之前父结点的指针发生了错误。这里会涉及到父亲结点是否需要删除的情况

具体情况见下图

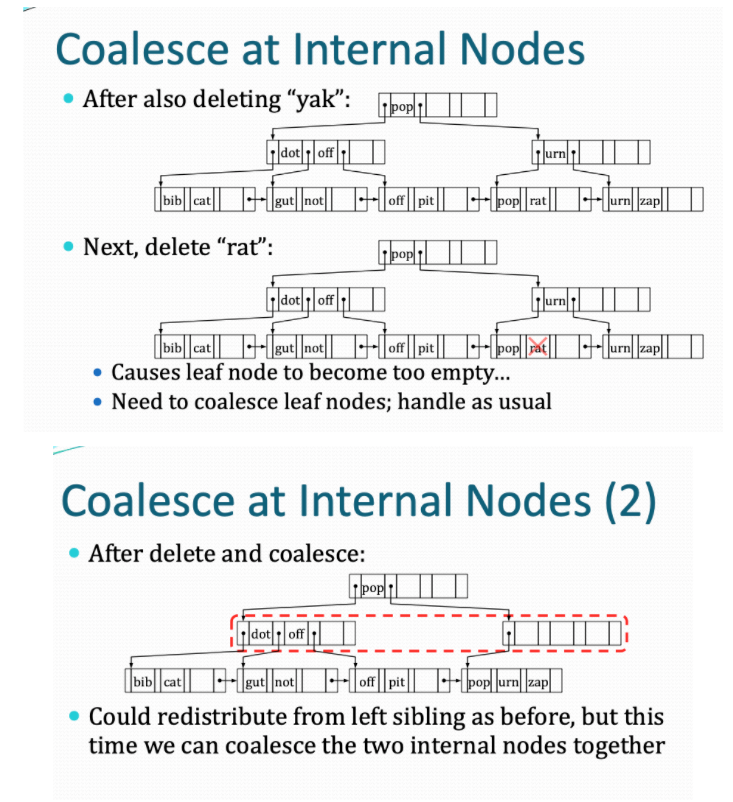
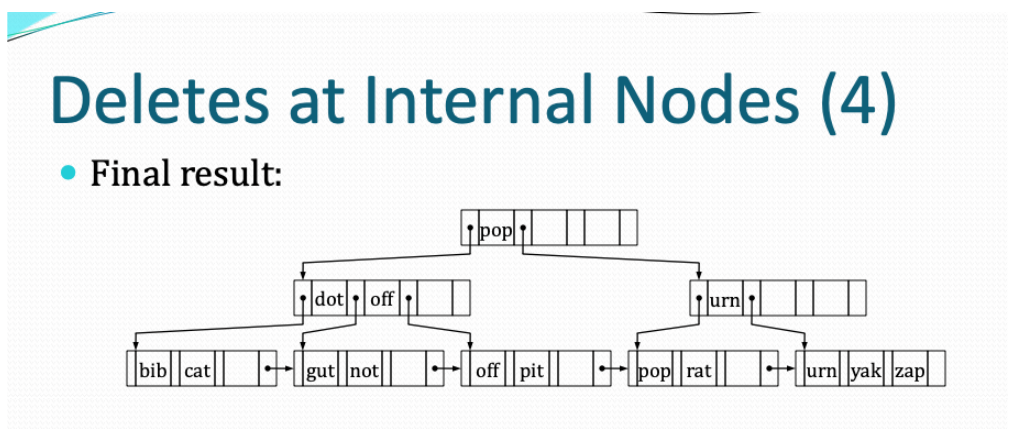
可能由于叶子结点的合并操作，导致父亲结点变成null空结点。或者说是其不满足最小结点个数要求。这样就要对父亲结点进行处理，这个时候是父亲结点也可以进行合并，这个时候原来的父亲结点就无了。合并之后的结果如下图

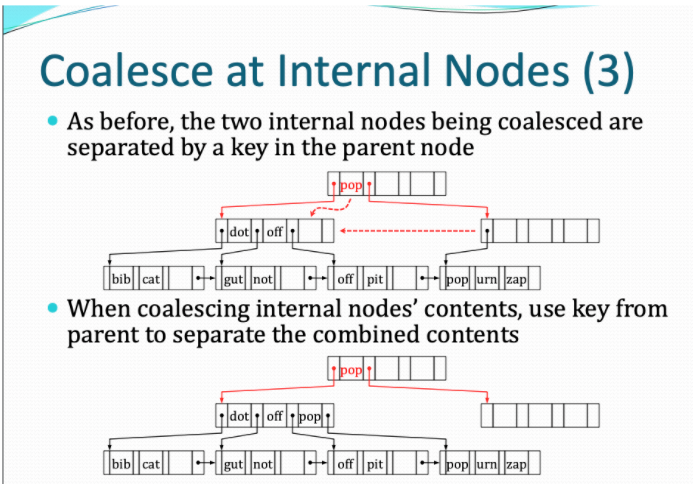
记得递归处理就好

INDEX_TEMPLATE_ARGUMENTS
template <typename N>
bool BPLUSTREE_TYPE::Coalesce(N **neighbor_node, N **node,
                              BPlusTreeInternalPage<KeyType, page_id_t, KeyComparator> **parent, int index,
                              Transaction *transaction) {
  // Assume that *neighbor_node is the left sibling of *node

  // Move entries from node to neighbor_node
  if ((*node)->IsLeafPage()) {
    LeafPage *leaf_node = reinterpret_cast<LeafPage *>(*node);
    LeafPage *leaf_neighbor = reinterpret_cast<LeafPage *>(*neighbor_node);

    leaf_node->MoveAllTo(leaf_neighbor);
    leaf_neighbor->SetNextPageId(leaf_node->GetNextPageId());
  } else {
    InternalPage *internal_node = reinterpret_cast<InternalPage *>(*node);
    InternalPage *internal_neighbor = reinterpret_cast<InternalPage *>(*neighbor_node);

    internal_node->MoveAllTo(internal_neighbor, (*parent)->KeyAt(index), buffer_pool_manager_);
  }

  buffer_pool_manager_->UnpinPage((*node)->GetPageId(), true);
  buffer_pool_manager_->DeletePage((*node)->GetPageId());

  (*parent)->Remove(index);

  // If parent is underfull, recursive operation
  if ((*parent)->GetSize() < minSize(*parent)) {
    return CoalesceOrRedistribute(*parent, transaction);
  }
  return false;
}

5. 叶子结点和内部结点对应的两个MoveAllTo函数

这个函数就不写了。实现比较简单，唯一要注意的就是对于内部结点的合并操作，要把需要删除的内部结点的叶子结点转移过去。也就是要有下面这样的一行

recipient->array_[recipient->GetSize()].first = middle_key;

3. Redistribute流程

当然也可以先看一下算法示意图。

下图是对叶子结点的的Redistribute函数

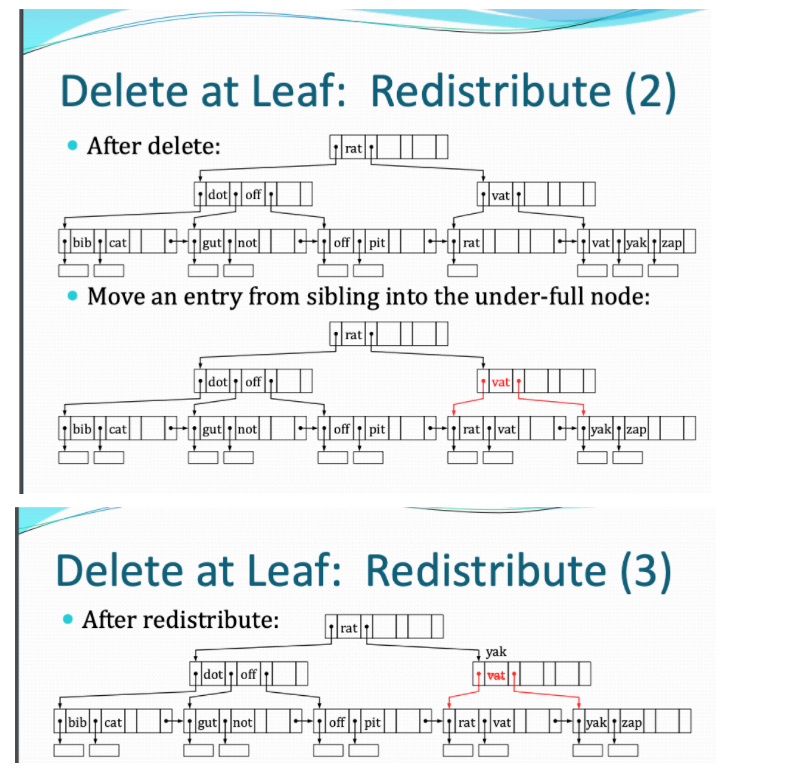
这里在移动的时候只要记得更新父亲对应index的key值就好了。

然而对于内部结点则并不是这么简单的情况了。内部结点可以直接从它的兄弟结点copy然后修改其根节点吗，这显然不合理。

对于这种情况的处理可以见下图

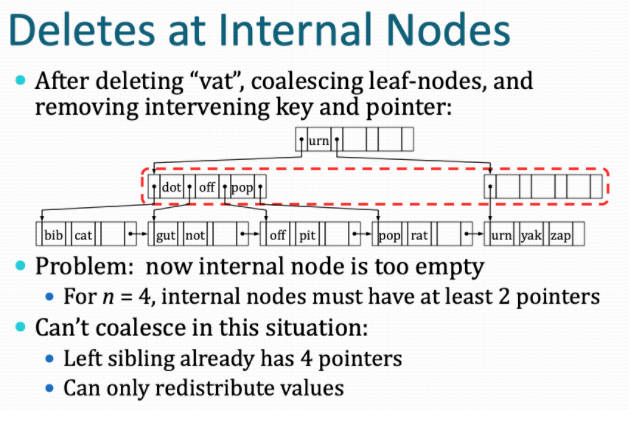
因此整个redistribute所涉及的四种情况就如下

1. 向叶子结点左边借
2. 向叶子结点右边借
3. 内部结点左边借
4. 内部结点右边借

1. 对于叶子结点向左边借的情况

好了删除算法已经实现了。首先我们可以通过test函数

cd build
make b_plus_tree_delete_test
./test/b_plus_tree_delete_test --gtest_also_run_disabled_tests

然后我们自己做一些test。这里我就拿一个例子来看

插入10、5、7、4、9得到下图是正确的

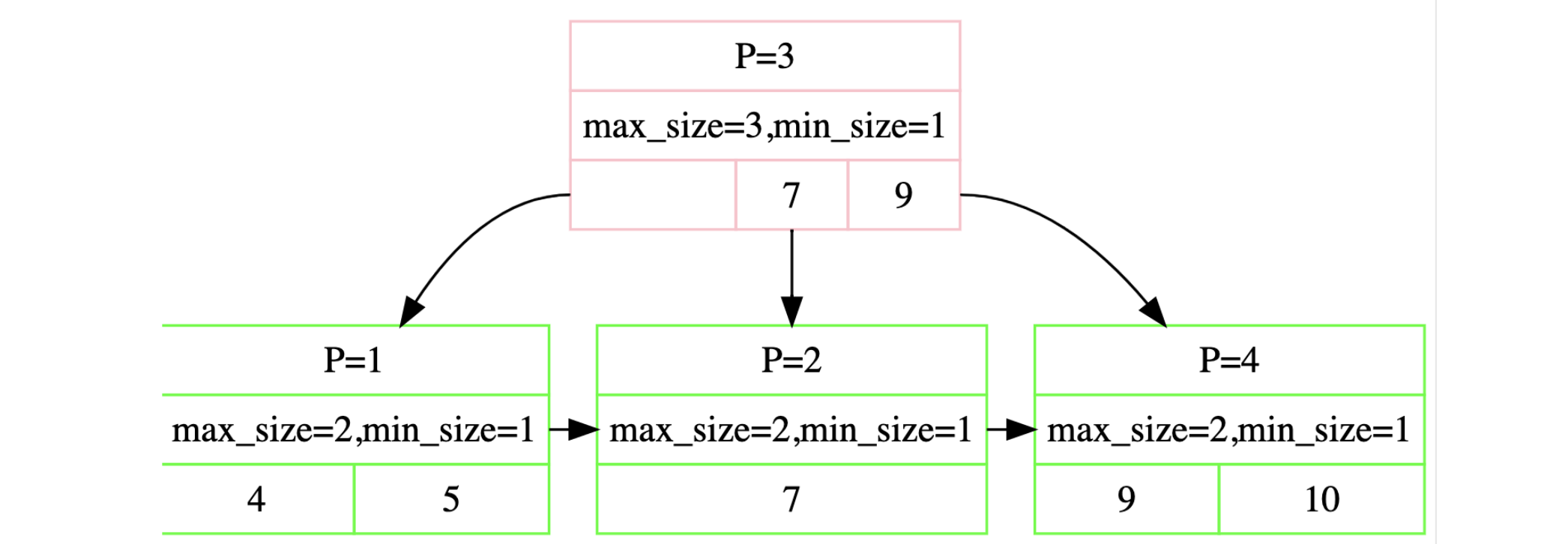
然后删除元素7

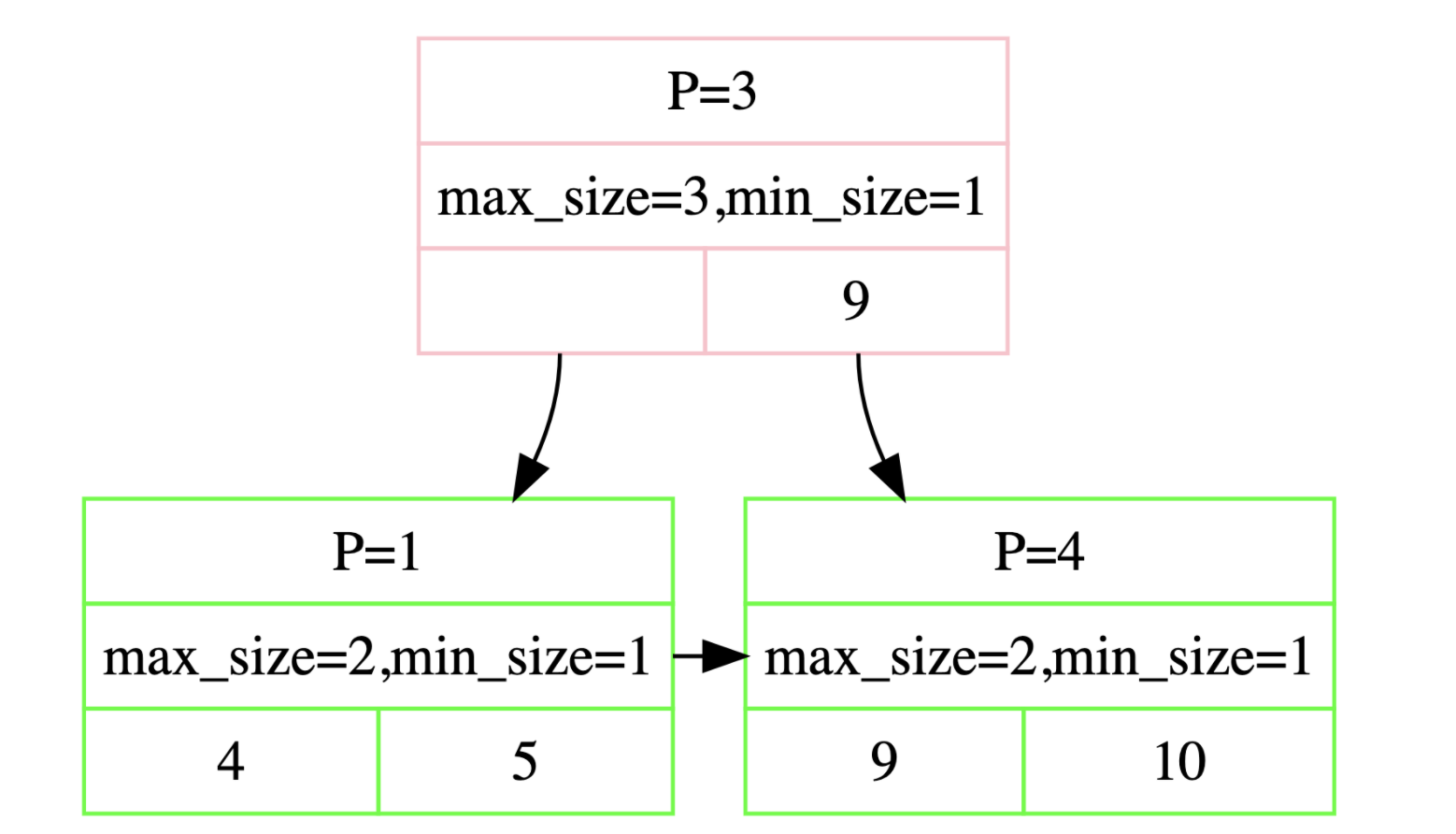
可以发现是完全正确的好了。第二部分就完成了。下面就是最后一部分对于的实现和迭代器的实现