这是why哥的第 83 篇原创文章

让人抠脑壳的 LFU

前几天在某APP看到了这样的一个讨论：

看到一个有点意思的评论：

LFU 是真的难，脑壳都给我抠疼了。

如果说 LRU 是 Easy 模式的话，那么把中间的字母从 R（Recently） 变成 F（Frequently），即 LFU ，那就是 hard 模式了。

你不认识 Frequently 没关系，毕竟这是一个英语专八的词汇，我这个英语八级半的选手教你：

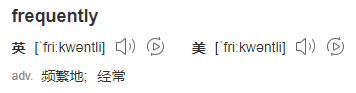
所以 LFU 的全称是Least Frequently Used，最不经常使用策略。

很明显，强调的是使用频率。

而 LRU 算法的全称是Least Recently Used。最近最少使用算法。

强调的是时间。

当统计的维度从时间变成了频率之后，在算法实现上发生了什么变化呢？

这个问题先按下不表，我先和之前写过的 LRU 算法进行一个对比。

LRU vs LFU

LRU 算法的思想是如果一个数据在最近一段时间没有被访问到，那么在将来它被访问的可能性也很小。所以，当指定的空间已存满数据时，应当把最久没有被访问到的数据淘汰。

也就是淘汰数据的时候，只看数据在缓存里面待的时间长短这个维度。

而 LFU 在缓存满了，需要淘汰数据的时候，看的是数据的访问次数，被访问次数越多的，就越不容易被淘汰。

但是呢，有的数据的访问次数可能是相同的。

怎么处理呢？

如果访问次数相同，那么再考虑数据在缓存里面待的时间长短这个维度。

也就是说 LFU 算法，先看访问次数，如果次数一致，再看缓存时间。

给大家举个具体的例子。

假设我们的缓存容量为 3，按照下列数据顺序进行访问：

如果按照 LRU 算法进行数据淘汰，那么十次访问的结果如下：

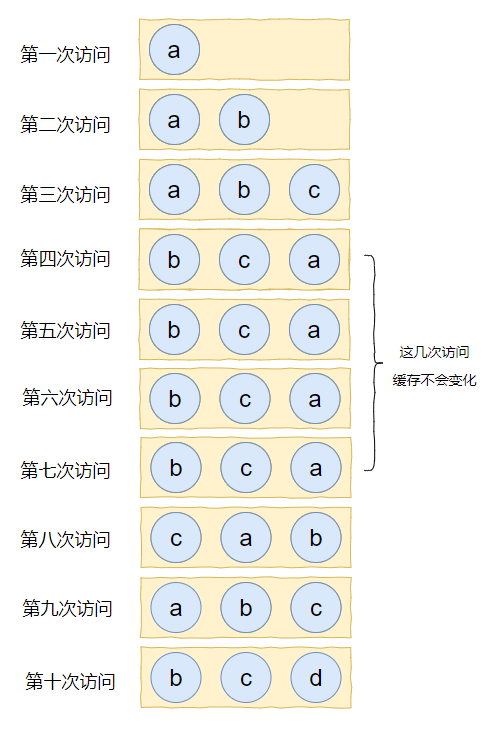
十次访问结束后，缓存中剩下的是 b，c，d 这三个元素。

你有没有觉得有一丝丝不对劲？

十次访问中元素 a 被访问了 5 次，结果最后元素 a 被淘汰了？

如果按照 LFU 算法，最后留在缓存中的三个元素应该是 b，c，a。

这样看来，LFU 比 LRU 更加合理，更加巴适。

假设，要我们实现一个 LFUCache：

class LFUCache {

    public LFUCache(int capacity) {

    }
    
    public int get(int key) {

    }
    
    public void put(int key, int value) {

    }
}

那么思路应该是怎样的呢？

带你瞅一眼。

LFU 方案一 – 一个双向链表

如果在完全没有接触过 LFU 算法之前，让我硬想，我能想到的方案也只能是下面这样的：

因为既需要有频次，又需要有时间顺序。

我们就可以搞个链表，先按照频次排序，频次一样的，再按照时间排序。

因为这个过程中我们需要删除节点，所以为了效率，我们使用双向链表。

还是假设我们的缓存容量为 3，还是用刚刚那组数据进行演示。

我们把频次定义为 freq，那么前三次访问结束后，即这三个请求访问结束后：

链表里面应该是这样的：

三个元素的访问频次都是 1。

对于前三个元素来说，value=a 是频次相同的情况下，最久没有被访问到的元素，所以它就是 head 节点的下一个元素，随时等着被淘汰。

接着过来了 1 个 value=a 的请求：

当这个请求过来的时候，链表中的 value=a 的节点的频率（freq）就变成了2。

此时，它的频率最高，最不应该被淘汰。

因此，链表变成了下面这个样子：

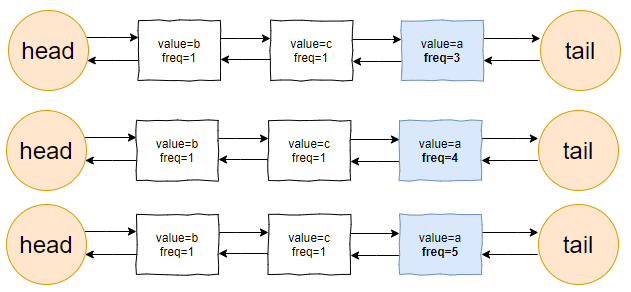
接着连续来了 3 个 value=a 的请求：

此时的链表变化就集中在 value=a 这个节点的频率（freq）上：

接着，这个 b 请求过来了：

b 节点的 freq 从 1 变成了 2，节点的位置也发生了变化：

然后，c 请求过来：

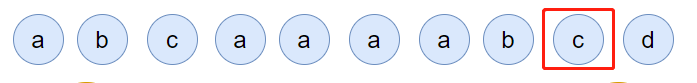
你说这个时候会发生什么事情？

链表中的 c 当前的访问频率是 1，当这个 c 请求过来后，那么链表中的 c 的频率就会变成 2。

你说巧不巧，此时，value=b 节点的频率也是 2。

撞车了，那么你说，这个时候怎么办？

前面说了：频率一样的时候，看时间。

value=c 的节点是正在被访问的，所以要淘汰也应该淘汰之前被访问的 value=b 的节点。

此时的链表，就应该是这样的：

然后，最后一个请求过来了：

d 元素，之前没有在链表里面出现过，而此时链表的容量也满了。

该进行淘汰了。

于是把 head 的下一个节点（value=b）淘汰，并把 value=d 的节点插入：

最终，所有请求完毕。

留在缓存中的是 d，c，a 这三个元素。

整体的流程就是这样的：

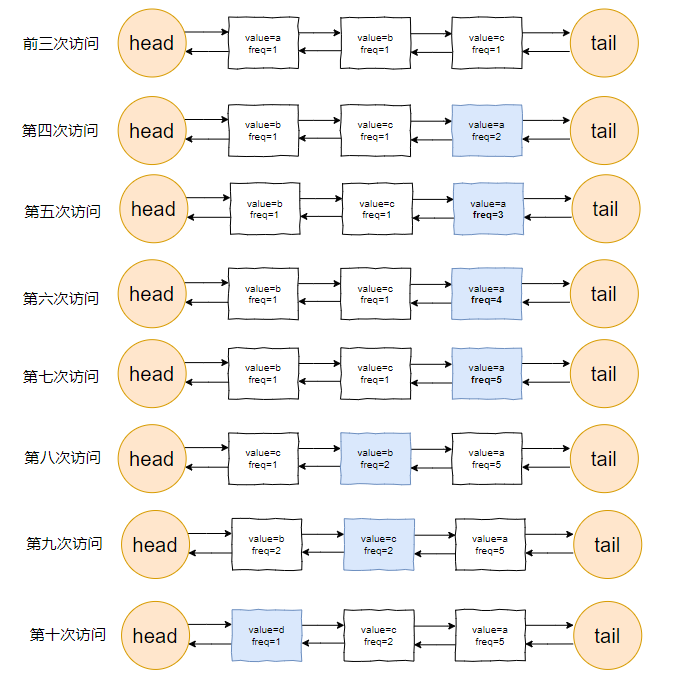
当然，这里只是展示了链表的变化。

其实我们放的是 key-value 键值对。

所以应该还有一个 HashMap 来存储 key 和链表节点的映射关系。

这个简单，用脚趾头都能想到，我也就不展开来说了。

按照上面这个思路，你慢慢的写代码，应该是能写出来的。

上面这个双链表的方案，就是扣着脑壳硬想，大部分人能直接想到的方案。

面试官要的肯定是时间复杂度为 O(1) 的解决方案。

现在的这个解决方案时间复杂度为 O(N)。

O(1) 解法

如果我们要拿出时间复杂度为 O(1) 的解法，我们就得细细的分析了，不能扣着脑壳硬想了。

先分析一下需求。

第一点：我们需要根据 key 查询其对应的 value。

用脚趾头都能想到，用 HashMap 存储 key-value 键值对。

查询时间复杂度为 O(1)，满足。

第二点：每当我们操作一个 key 的时候，不论是查询还是新增，都需要维护这个 key 的频次，记作 freq。

因为我们需要频繁的操作 key 对应的 freq，也就是得在时间复杂度为 O(1) 的情况下，获取到指定 key 的 freq。

来，请你大声的告诉我，用什么数据结构？

是不是还得再来一个 HashMap 存储 key 和 freq 的对应关系？

第三点：如果缓存里面放不下了，需要淘汰数据的时候，把 freq 最小的 key 删除掉。

注意啊，上面这句话：[把 freq 最小的 key 删除掉]。

freq 最小？

我们怎么知道哪个 key 的 freq 最小呢？

前面说了，有一个 HashMap 存储 key 和 freq 的对应关系。

当然我们可以遍历这个 HashMap，来获取到 freq 最小的 key。

但是啊，朋友们，遍历出现了，那么时间复杂度还会是 O(1) 吗？

那怎么办呢？

注意啊，高潮来了，一学就废，一点就破。

我们可以搞个变量来记录这个最小的 freq 啊，记为 minFreq，不就行了？

现在我们有最小频次（minFreq）了，需要获取到这个最小频次对应的 key，时间复杂度得为 O(1)。

来，朋友，请你大声的告诉我，你又想起了什么数据结构？

是不是又想到了 HashMap？

好了，我们现在有三个 HashMap 了，给大家介绍一下：

• 一个存储 key 和 value 的 HashMap，即HashMap<key,value>。
  
• 一个存储 key 和 freq 的 HashMap，即HashMap<key,freq>。
  
• 一个存储 freq 和 key 的 HashMap，即HashMap<freq,key>。
  

它们每个都是各司其职，目的都是为了时间复杂度为 O(1)。

但是我们可以把前两个 HashMap 合并一下。

我们弄一个对象，对象里面包含两个属性分别是value、freq。

假设这个对象叫做 Node，它就是这样的，频次默认为 1：

class Node {
    int value;
    int freq = 1;
    //构造函数省略
}

那么现在我们就可以把前面两个 HashMap ，替换为一个了，即 HashMap<key,Node>。

同理，我们可以在 Node 里面再加入一个 key 属性：

class Node {
    int key;
    int value;
    int freq = 1;
    //构造函数省略
}

因为 Node 里面包含了 key，所以可以把第三个 HashMap<freq,key> 替换为 HashMap<freq,Node>。

到这一步，我们还差了一个非常关键的信息没有补全，就是下面这一个点。

第四点：可能有多个 key 具有相同的最小的 freq，此时移除这一批数据在缓存中待的时间最长的那个元素。

这个需求，我们需要通过 freq 查找 Node，那么操作的就是 HashMap<freq,Node> 这个哈希表。

上面说[多个 key 具有相同的最小的 freq]，也就是说通过 minFreq ，是可以查询到多个 Node 的。

所以HashMap<freq,Node> 这个哈希表，应该是这样的：

HashMap<freq,集合 >。

此时的问题就变成了：我们应该用什么集合来装这个 Node 对象呢？

不慌，我们先理一下这个集合需要满足什么条件。

首先，需要删除 Node 的时候。

因为这个集合里面装的是访问频次一样的数据，那么希望这批数据能有时序，这样可以快速的删除待的时间最久的 Node。

有时序，能快速查找删除待的时间最久的 key，你能想到什么数据结构？

这不就是双向链表吗？

然后，需要访问 Node 的时候。

一个 Node 被访问，那么它的频次必然就会加一。

比如下面这个例子：

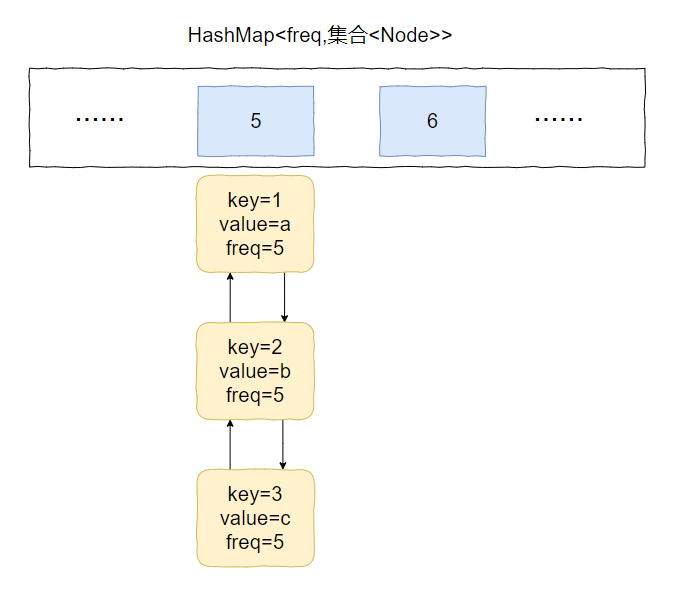
假设最小访问频次就是 5，而 5 对应了 3 个 Node 对象。

此时，我要访问 value=b 的对象，那么该对象就会从 key=5 的 value 中移走。

然后频次加一，即 5+1=6。

加入到 key=6 的 value 集合中，变成下面这个样子：

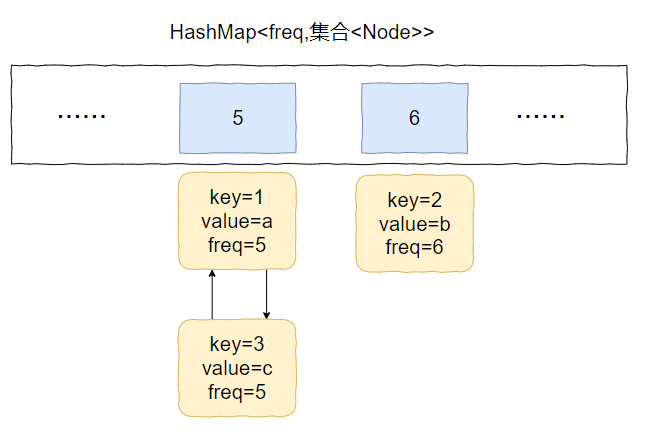
也就是说我们得支持任意 node 的快速删除。

我们可以针对上面的需求，自定义一个双向链表。

但是在 Java 集合类中，有一个满足上面说的有序且支持快速删除的条件的集合。

那就是 LinkedHashSet。

所以，HashMap<freq,集合 >，就是HashMap<freq,LinkedHashSet >。

总结一下。

我们需要两个 HashMap，分别是 HashMap<key,Node> 和 HashMap<freq,LinkedHashSet >。

然后还需要维护一个最小访问频次，minFreq。

哦，对了，还得来一个参数记录缓存支持的最大容量，capacity。

没了。

有的小伙伴肯定要问了：你倒是给我一份代码啊？

这些分析出来了，代码自己慢慢就撸出来了。

思路清晰后再去写代码，就算面试的时候没有写出 bug free 的代码，也基本上八九不离十了。

Dubbo 中的 LFU 算法

Dubbo 在 2.7.7 版本之后支持了 LFU 算法：

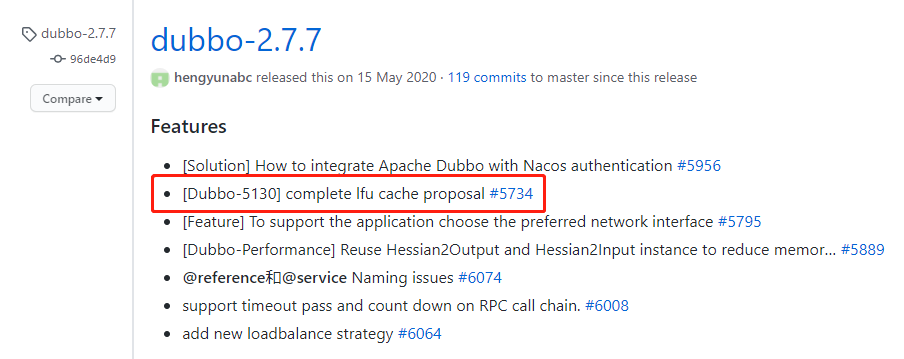
其源码的位置是：org.apache.dubbo.common.utils.LFUCache

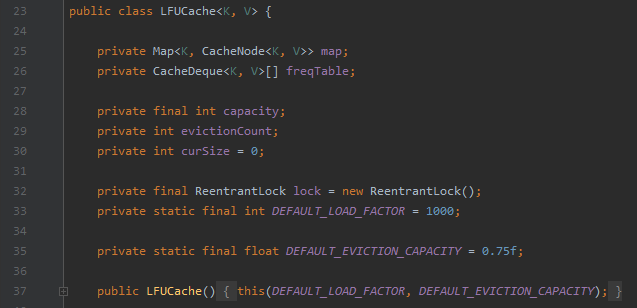
代码不长，总共就 200 多行，和我们上面说的 LFU 实现起来还有点不一样。

你可以看到它甚至没有维护 minFreq。

但是这些都不重要，打个断点调试一下很快就能分析出来作者的代码思路。

重要的是，我在看 Dubbo 的 LFU 算法的时候发现了一个 bug。

不是指这个 LFU 算法实现上的 bug，算法实现我看了是没有问题的。

bug 是 Dubbo 虽然加入了 LFU 缓存算法的实现，但是作为使用者，却不能使用。

问题出在哪里呢？

我带你瞅一眼。

源码里面告诉我这样配置一下就可以使用 lfu 的缓存策略：

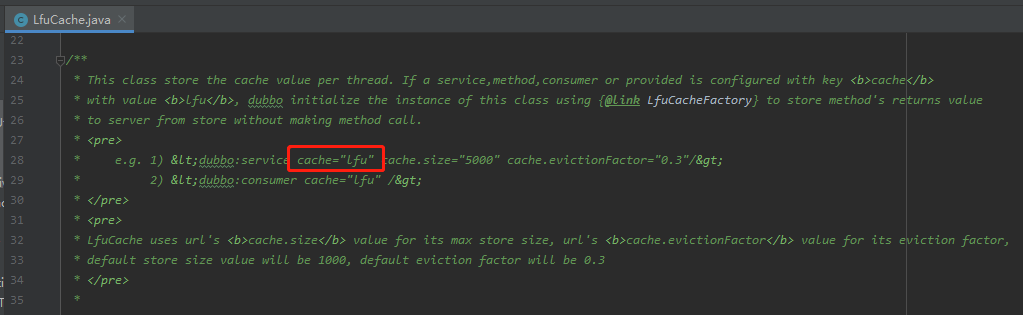
但是，当我这样配置，发起调用之后，是这样的：

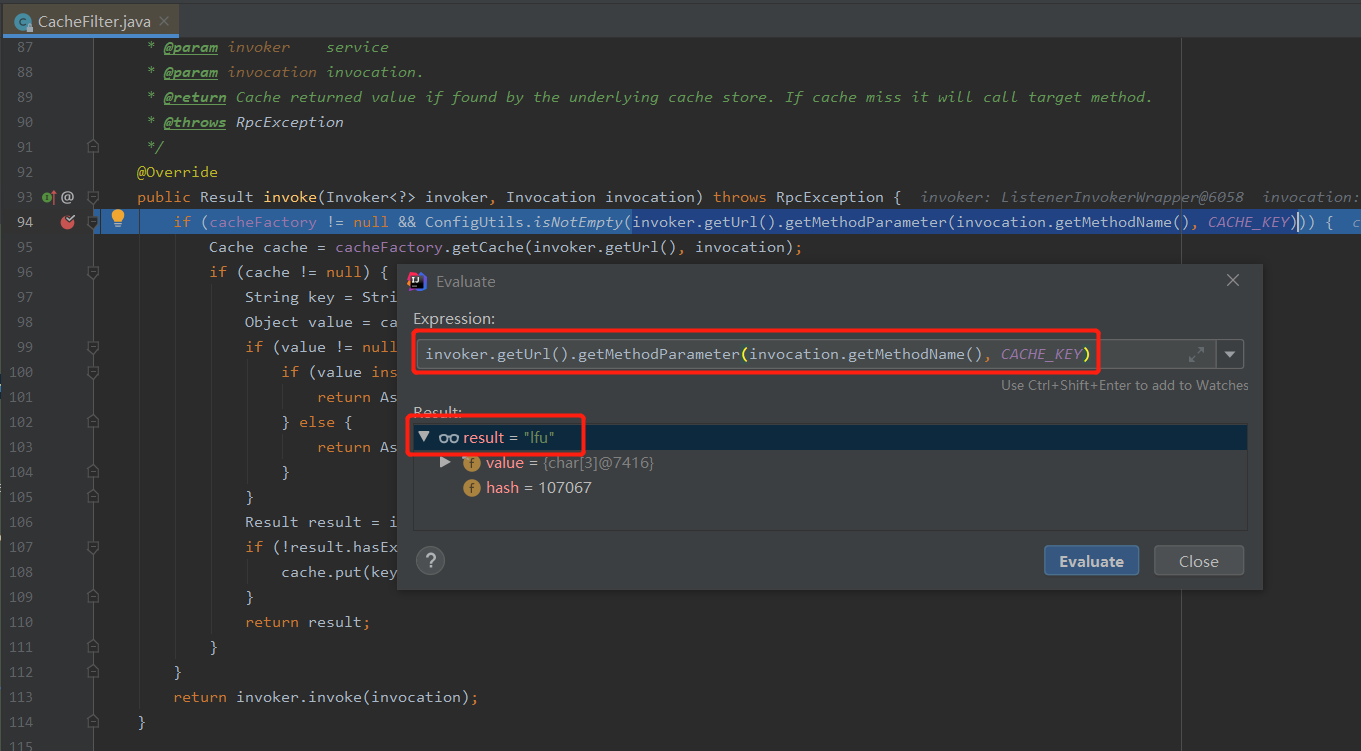
可以看到当前请求的缓存策略确实是 lfu。

但是会抛出一个错误：

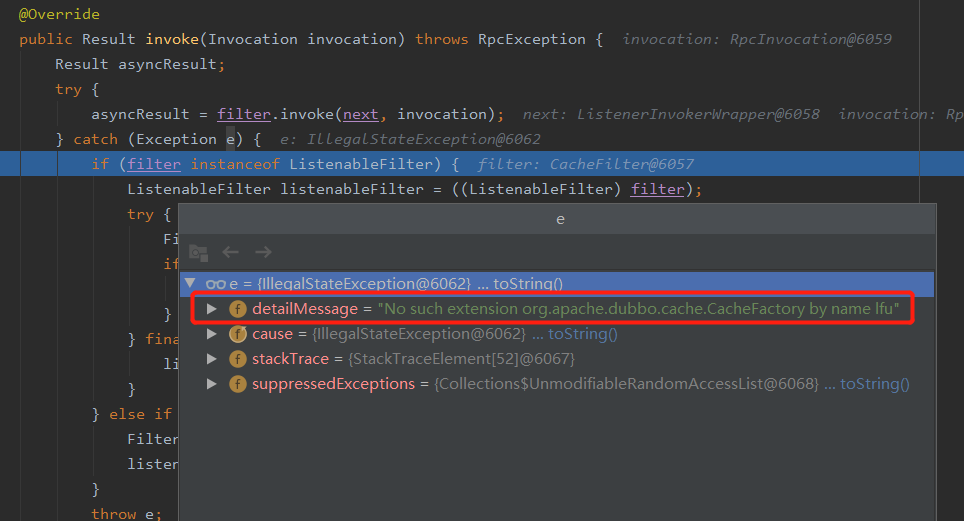
No such extension org.apache.dubbo.cache.CacheFactory by name lfu

没有 lfu 这个策略。

这不是玩我吗？

再看一下具体的原因。

在org.apache.dubbo.common.extension.ExtensionLoader#getExtensionClasses处只获取到了 4 个缓存策略，并没有我们想要的 LFU:

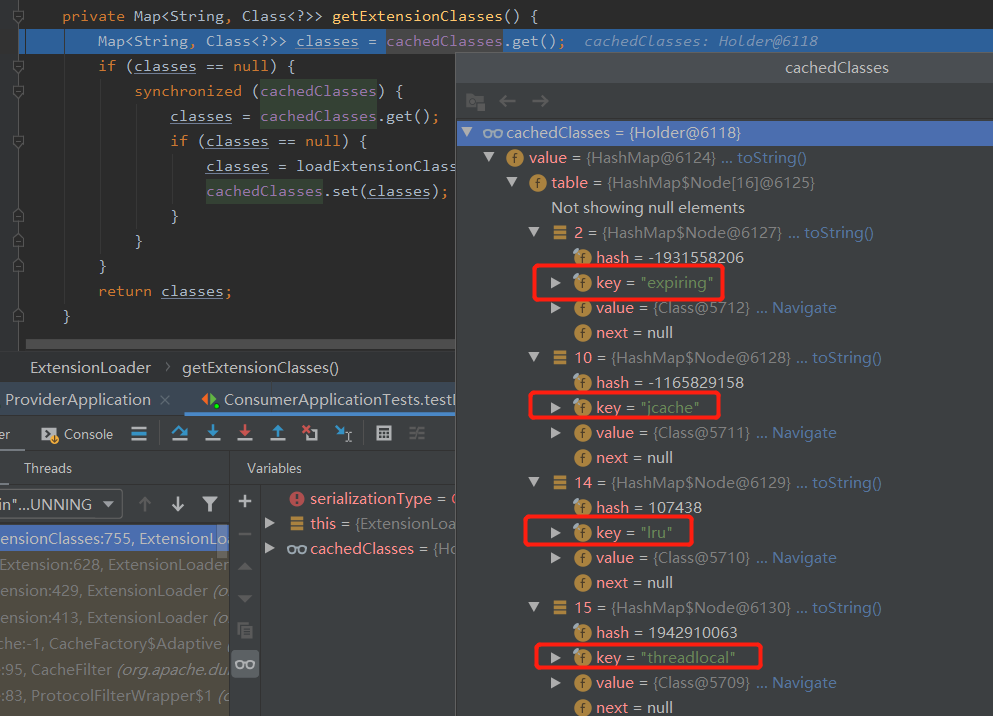
所以，在这里抛出了异常：

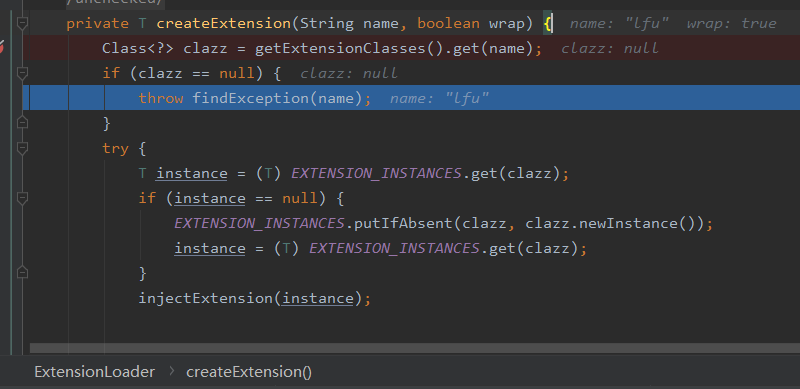
为什么没有找到我们想要的 LFU 呢？

那就的看你熟不熟悉 SPI 了。

在 SPI 文件中，确实没有 lfu 的配置：

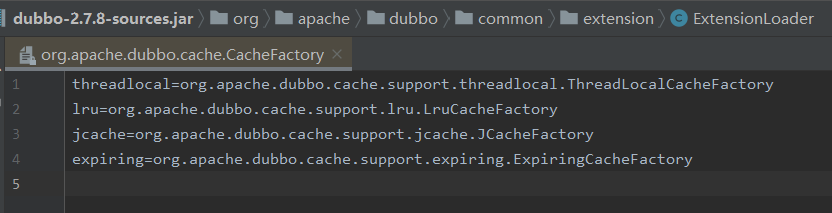
这就是 bug。

所以怎么解决呢？

非常简单，加上就完事了。

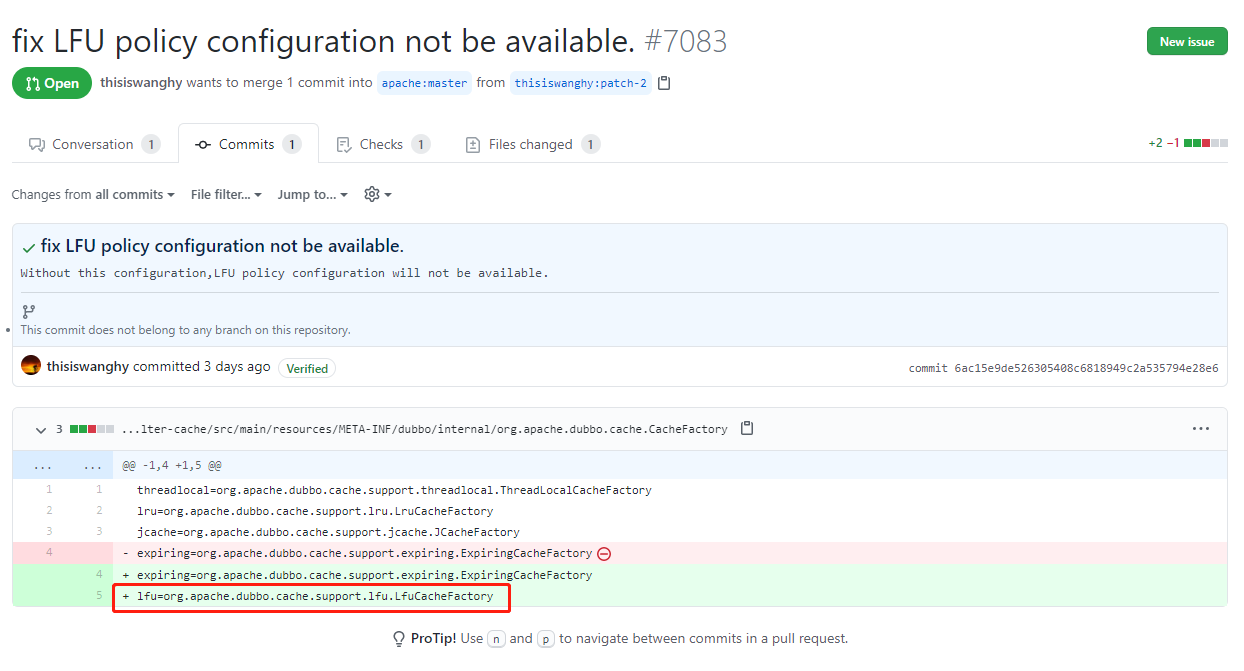
害，一不小心又给 Dubbo 贡献了一行源码。

最后说一句（求关注）

才疏学浅，难免会有纰漏，如果你发现了错误的地方，可以在后台提出来，我对其加以修改。

感谢您的阅读，我坚持原创，十分欢迎并感谢您的关注。

我是 why，一个主要写代码，经常写文章，偶尔拍视频的程序猿。