一、概述

机器人运动学研究的是机械臂各个连杆之间的位移关系、速度关系和加速度关系。比较经典的一本书推荐大家读读熊有伦的《机器人技术基础》下载网址在这。本篇博文将从刚体的位姿描述讲起，逐步过渡到D-H法运动学建模的方法与步骤，结合前几篇博客所树的Rob机器人的手臂建立D-H运动学模型，并编写一个逆运动学运动学求解的程序。  

（1）位姿描述

我们知道，刚体在世界坐标系里需要通过位置和姿态两个维度来描述。首先，位置描述很容易理解，就是坐标，例如点P的位姿通过坐标P_x，P_y，P_z来描述，如下所示。   目前它是三维形式，但是我们需要在其下面添加一维，使其变为四维形式，如下所示，这就是齐次坐标，多增加的这一维 ω 称为比例因子，这里取1。   姿态的描述的描述相对复杂一些，它表征的是刚体相对于世界坐标系的旋转情况，我们首先需要在刚体上添加一个坐标系，用这个坐标系的姿态来代表刚体的姿态，如图一所示，在世界坐标系中的刚体，我们建立坐标系X’，Y’，Z’，然后分别额在这个坐标系上取单位失向量n，o，b。   刚体上的每个坐标轴 X’，Y’，Z’ 都和世界坐标轴 X, Y, Z 之间在空间上存在夹角，我们以这些夹角为基础对其姿态进行描述，便得到下面这个式子，矩阵 R 就是刚体相对于世界坐标系的姿态描述。此外还有其他的描述方法，比如欧拉角描述方法，四元数描述方法等。   我们将上面的 R 矩阵由三行三列的矩阵变换为四行三列的矩阵，最后一行补零，就得到了刚体姿态的其次矩阵，然后在将位置齐次矩阵加入进来组成四行四列的矩阵，就是刚体位姿描述的整体矩阵：T（也可以称为转换矩阵），如下式：   我们也可以将其理解为这是相邻的两个坐标系之间的转换关系或相对关系，只是这个相对关系通过位置和姿态两个维度来描述的。我们的机械臂是由一系列杆件和运动关节组成，如果我们以一定的规则在机械臂的关节处建立坐标系，就得到一系列的坐标系，如图2所示，如果我们又知道这一系列坐标系中每相邻两个的转换关系（即转换矩阵），那么通过推导我们就知道了首位两个坐标系之间的转换关系了，从而就可以实现机械臂的运动学描述了。 图2  

（2）正逆运动学

我们知道机器人运动学研究的是连杆之间的位移关系、速度关系和加速度关系，它又分为正运动学和逆运动学。   正运动学：知道机械臂各个关节的关节变量（如每个转动关节转了多少度，移动关节移动了对少距离）推导出末端执行器相对于世界坐标系的位姿关系（坐标系n相对坐标系0）。（解决的是我在哪的问题）   逆运动学：知道末端执行器相对于世界坐标系的位姿关系（坐标系n相对坐标系0），推导出要到达这个位姿械臂各个关节的关节变量（如每个转动关节需要转多少度，移动关节需要移动多少距离）。（解决的是如何到那的问题）  

二、D-H法

通过第一部分我们就可以分析知道，所谓的机器人运动学建模通俗讲分为以下几个步骤:   1. 以一定的规则在机械臂上创建一系列的坐标系。 2. 通过这些坐标系中每相邻两个坐标系之间的关系推导出最后一个坐标系（坐标系n）相对于第一个坐标系（坐标系0）的转换关系（转换矩阵）。 3. 通过这个转换关系获得机械臂正运动学矩阵。 4. 通过正运动学矩阵获得逆运动学的求解方法。   具体以什么样的规则创建坐标系？如何才能快速获得两个相邻坐标系之间的转换关系？如何求取逆运动学解？这一些列问题早在1995年两位前辈就给出了答案（膜拜，经典的东西往往经久不衰），它们就是 Denavit 和 Hartenberg，（业内简称D-H法）下面我们一步步看看它们如何解决这些问题的。

（1）描述连杆和连杆连接的参数

上述两位大师将相邻两个连杆（刚体）之间的关系简化成4个参数来描述，其中另个参数用来描述连杆，两个参数用来描述两个连杆的连接关系，先来说说描述连杆的两个参数：a_i-1 和 α_i-1 ，如图3所示。 图3   Link length 连杆长度 a_i-1 ，关节轴 i-1 和关节轴 i 之间的公垂线（图3红色直线）的长度a_i-1。   Link twist   连杆转角 α_i-1，假设作一个平面,并使该平面与两关节轴之间的公垂线垂直（图3粉红色平面）,然后把关节轴 i-1 和关节轴 i 投影到该平面上,在平面内轴 i-1 按照右手法则转向轴 i ，测量两轴角之间的夹角为α_i-1.   再看一下描述两个连杆的连接关系的两个参数 d_i 和 θ_i，如图4所示。 图4   link offset 连杆偏距 d_i，相邻两个连杆之间有一个公共的关节, 沿着两个相邻连杆公共法线（图4两条黄线）的距离可以用一个参数描述为连杆偏距d_i。（当 i 为移动关节时,连杆偏距为一变量）   joint angle 关节角 θ_i， 两个相邻连杆的两条公共法线（图4两条黄线）绕公共轴线（图4红色轴线）旋转的夹角（图4蓝色夹角） θ_i。   用这四个参数就可以完成相邻两个连杆（刚体）之间的关系的描述。  

（2）在机械臂上建立坐标系

Denavit 和 Hartenberg 确定了连杆关系的描述方法之后，又制定了坐标系的建立规则，长坐标系{0}到坐标系{n}的确定步骤如下：   a. 确定关节轴，并画出轴的延长线。 b. 找出关节轴 i -1 和 i 的公垂线（图3红色直线）关节轴 i -1 的交点 ，作为坐标系 i-1 的原点 O_i-1。 c. 规定 Z_i-1 的指向是沿着第 i-1 个关节轴。 d. 规定 X_i-1 轴的指向是沿着轴 i-1 和 i 的公垂线（图3红色直线）的方向，如果关节轴 i-1 和 i 相交，则X_i-1轴垂直于关节轴 i-1 和 i 所在的平面。 e. Y_i-1轴的方向由右手定则确定 Y_i-1 =  Z_i-1 × X_i-1 。   此外，对于坐标系{0} ，Z0轴沿着关节轴1的方向,当坐标系{1}的关节变量为0时，设定参考坐标系{0}与{1}重合，且a₀=0, α₀=0，当关节1为转动关节，d₁=0；当关节1为移动关节，θ₁=0。   坐标系{n} 通常规定:   对于转动关节 n，设定θ_n=0，此时 X_n 和 X_n-1 轴的方向相同，选取坐标系{n} 的原点位置,使之满足 d_n=0; 对于移动关节 n， 设定Xn轴的方向使之满足θ_n=0，当d_n=0时,选取坐标系{n} 的原点位于X_n-1轴与关节轴n的交点位置。  

 （3）根据机械臂上所建立的坐标系确定描述连杆和连杆连接的参数

建立完坐标系以后，就需要根据坐标系来确定小节（1）中所说的描述连杆和连杆连接的四个参数，由于我们是根据特定规则来建立的坐标系，所以我们很容易得到四个参数，得到的方法如图5所示。   图5  

 三、Rob手臂的D-H法建模

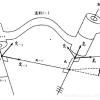
下面我们解结合前面博文所介绍的Rob机器人的一个手臂，讲解如何在它的手臂上建立坐标系，获得描述参数，最后得到运动学关系，首先手臂的模型抽象如下图6所示。   为了方便起见，我们让手臂抬起来伸直，如图7所示，这样方便我们建立坐标系，然后我们按照第二部分的（2）小节介绍的方法建立坐标系，首先绘制关节轴线（关节转轴） i₁ 到 i₅（图7中绿色虚线），然后根据规则确定原点 O₁ 到 O₆的位置，然后确定每个坐标系Z轴的方向（图7红色轴，和关节轴线共线），然后确定各个坐标系的X轴，最后根据右手定则确定各个坐标系的Y轴，此外各个连杆的物理尺寸如图7中的蓝色虚线所标识。 图7 （图画的太丑，没有美术细胞。。。-_-||）   一旦确定了坐标系，我们根据第二部分的（3）小节中图5所示的法则就可以快速确定每个连杆（坐标系）之间的描述参数，如下表所示。   至此其实我们已经得到了Rob手臂上的坐标系{0}到坐标系{6}之间每两个相邻坐标系的转换关系了，就是上表中 i 行的数据。但是拿到这些数据怎么转换成第一部分的（1）小节中所介绍的转换矩阵 T 呢？如何根据两个相邻坐标系的转换关系得到坐标系{6}到坐标系{0}的转换关系呢？又如何求取逆运动学解呢？这几个问题在下一篇博客中揭晓，并给出逆运动学求解的C++源代码。   <– 本篇完 –>