写在前面
之前考研的时候csapp的书有刷过5,6遍,所以对书本知识还算比较了解。恰逢最近在学c++的时候,顺带刷一下大名鼎鼎的csapp实验。
0. 环境准备
最好准备一个纯净的Linux系统这里建议使用docker 构建一个centos或者 ubuntu系统
实验资料的下载
CS:APP3e, Bryant and O’Hallaron
docker上的环境搭建请参考下面的文章
CSAPP:Lab0-搭载环境
拉取centos系统
docker pull centos
建立目录挂载实现文件同步
docker container run -it -v /Users/xxxx/yourFilePath:/csapp --name=csapp_env centos /bin/bash
/Users/xxxx/yourFilePath 请替换成你自己想要进行同步的目录
:/csapp 也请替换成你自己想要命名的目录
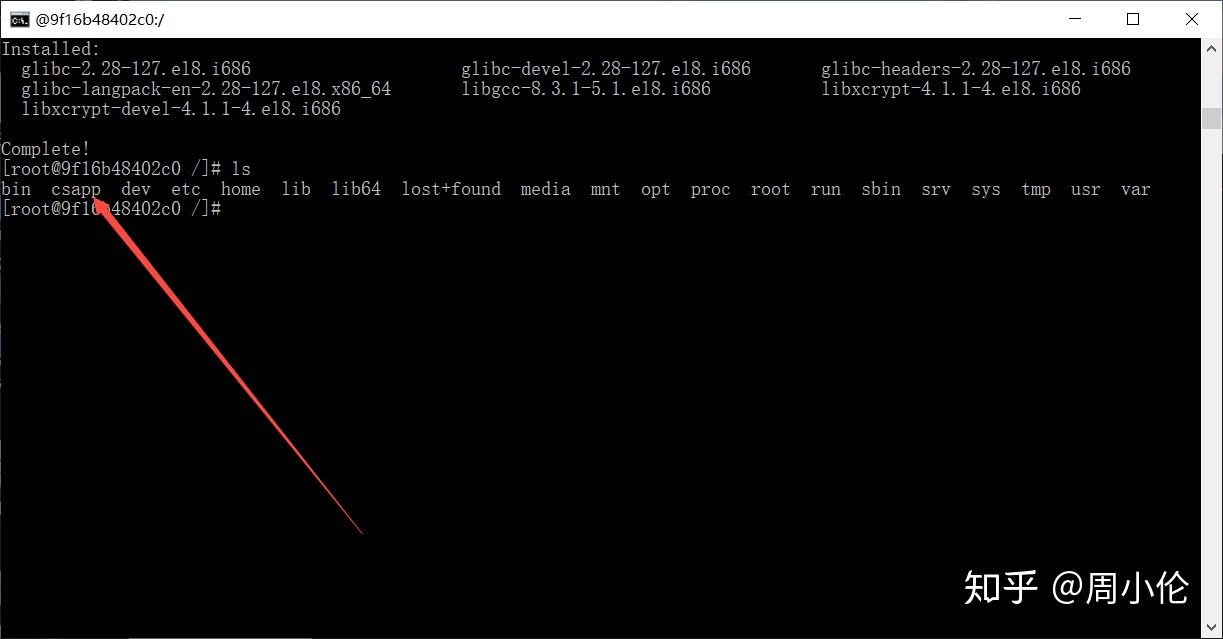
这里的csapp目录就是和你本地目录同步的目录
同步完成之后可以发现在docker下的csapp目录和我们的yourFilePath文件实现了同步


出现类似上面的结果则为配置正确
- 配置编译环境
- 更新yum源
yum -y update - 安装sudo
yum install sudo - 安装c/c++编译环境
yum install make automake gcc gcc-c++ kernel-devel - 安装gdb
yum install gdb - 准备32位嵌入式c库
yum install glibc-devel.i686 - 阅读readme 完成配置
这里需要先进入刚才映射的文件目录csapp文件然后参考readme文件
shell To compile and run the btest program, type:
unix> make btest
unix> ./btest [optional cmd line args]
完成上面的操作之后我们的配置就算完成了。
接下来我们可以在本机的编译器编写我们的代码。然后在docer中的虚拟容器上编译和运行我们的代码。
在编译器中编写
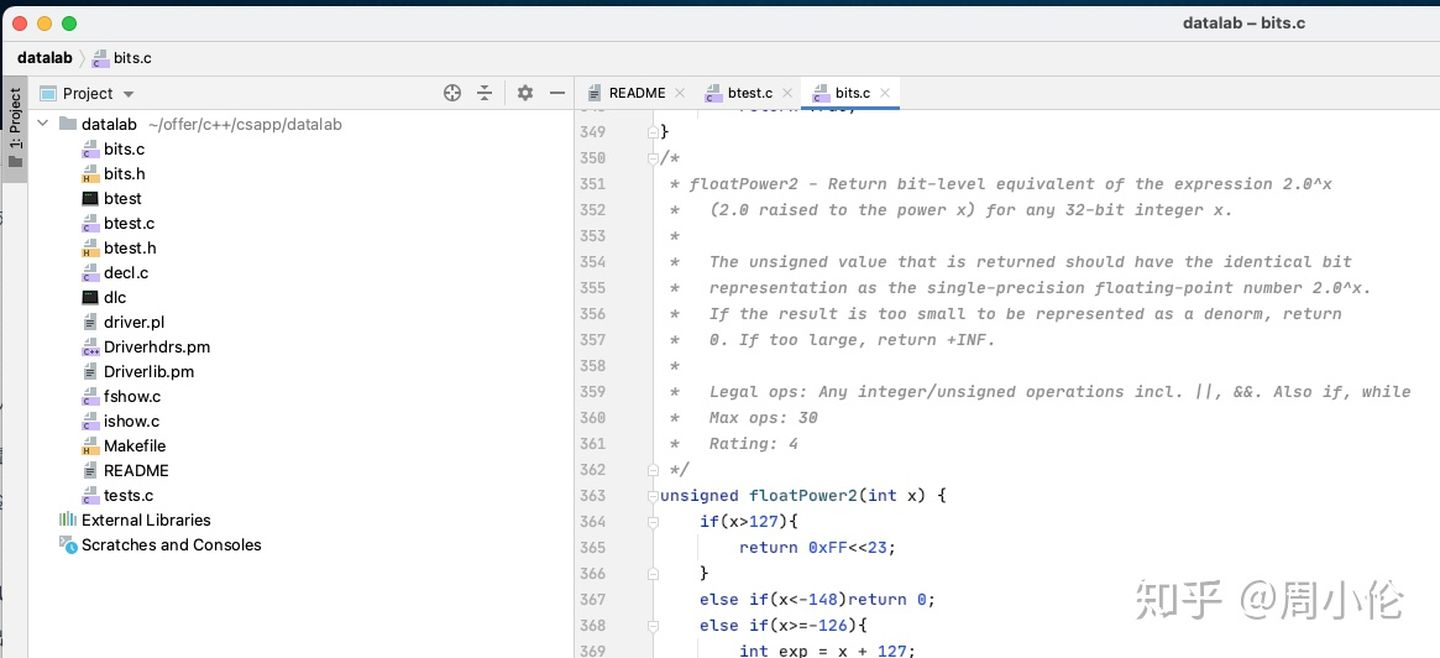
在docker容器中编译和运行
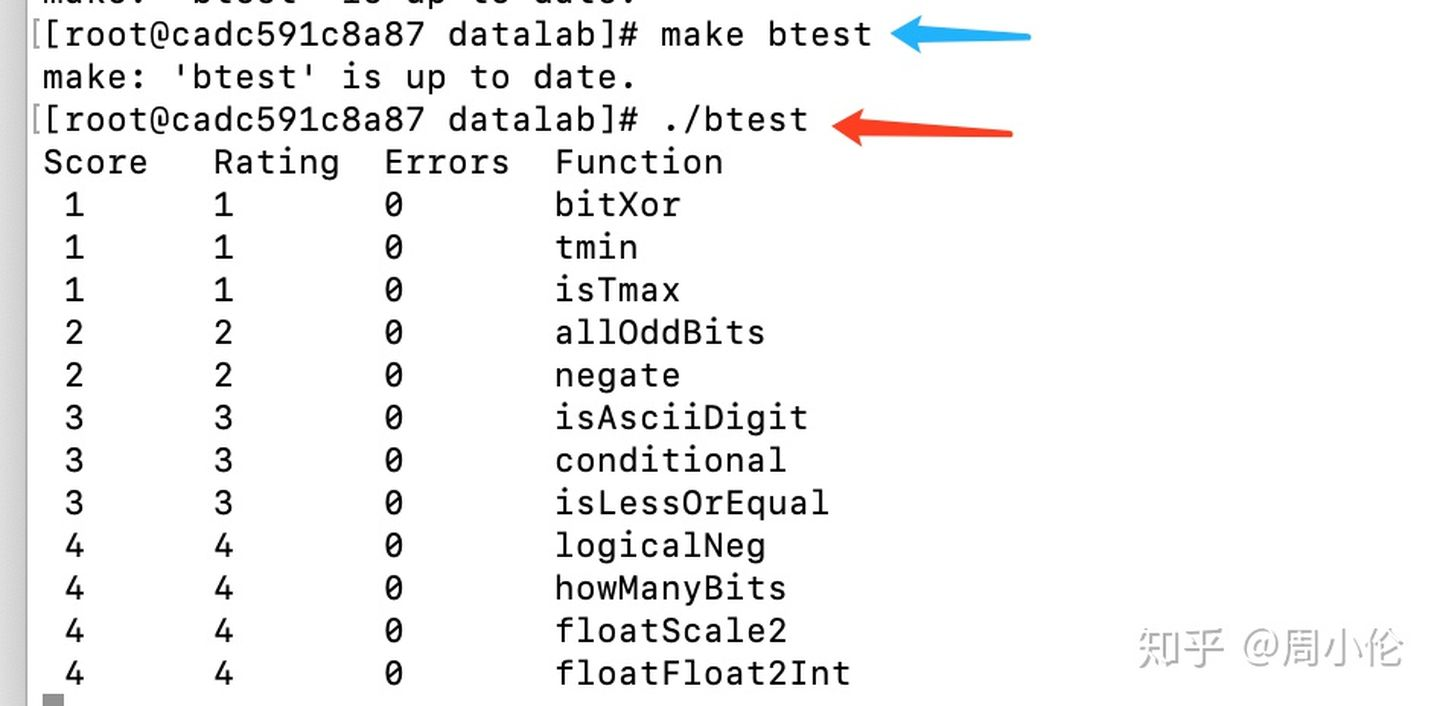
蓝色箭头为编译。红色箭头为运行
注意:每次更改bits.c文件后都要重新编译btest。如果需要检查单个函数的正确性,可以使用-f标志:
text $ ./btest -f bitXor
dlc程序可以检测我们有没有违规,如果运行没有输出则没有问题
text $ ./bits.c
注意每次关闭docker在下一次运行的时候需要先启动我们的centos。
先找到我们命名为csapp_env容器的容器id

-
然后docker start 容器ID启动我们的容器
-
输入以下命令进入到这个运行中的容器
docker exec -it 容器id /bin/bash
1. 实验开始
* IMPORTANT. TO AVOID GRADING SURPRISES:
* 1. Use the dlc compiler to check that your solutions conform
* to the coding rules.
* 2. Use the BDD checker to formally verify that your solutions produce
* the correct answers.
*/
1.1 bitXor
a^b=
1.(a|b)&(~a|~b)
2.~(~a&~b)&~(a&b)
3.(a&~b)|(~a&b)
可以用这三种方式表示异或操作,具体的推导可以自行Google,参考离散数学我自己推了一下发现其实不难
主要是对德摩根律的应用
\[ \begin{align} A\bigoplus B & = \overline{\overline AB\cup A \overline B} \\ & = \overline{(A \cup \overline B)\cap (\overline A \cup B}) \\ & = ( \overline{(A \cup \overline B)\cap \overline A )\cup ( (A \cup \overline B)\cap B )}\\ & = \overline{(\overline A \overline B) \cup( A B)} \\ & =\overline{(\overline A \overline B)}\cap \overline{( A B)}\\ \end{align} \]
我们选择第二种操作即可过掉本例
int bitXor(int x, int y) {
return ~(~x&~y)&~(x&y);
}
1.2 tmin
int tmin(void) {
return 1<<31;
}
1.3 tmax
题目描述
* isTmax - returns 1 if x is the maximum, two's complement number,
* and 0 otherwise
* Legal ops: ! ~ & ^ | +
* Max ops: 10
* Rating: 1
*/
思路
我们考虑四位的最大值x=0111 然后x+1之后就会变成1000 我们对1000 取非 0111 就会重新变回x值
这里要是可以用等于是不是直接完成了,但是不能用等于,在这可以用一个位运算的小技巧,我们知道自己与自己异或会得到0,也就是说我们可以用异或来判断等于!((~(x+1)^x)) 判断这个是否为1即可判断是否为最大值
这里有一个例外就是x=-1 由于-1=1111 他利用上面的式子判断也符合,故要特判-1 利用!!(x+1) 这个操作-1和最大值并不相同
int isTmax(int x) {
return !((~(x+1)^x))&!!(x+1);
}
1.4 allOddBits
/*
* allOddBits - return 1 if all odd-numbered bits in word set to 1
* where bits are numbered from 0 (least significant) to 31 (most significant)
* Examples allOddBits(0xFFFFFFFD) = 0, allOddBits(0xAAAAAAAA) = 1
* Legal ops: ! ~ & ^ | + << >>
* Max ops: 12
* Rating: 2
*/
思路
A=1010 A是一个典型的偶数位都是1的数,那只要一个四位的二进制数X & A = A 就说明这个二进制符合条件。那其实只要判断x & 0xAAAAAAAA == 0xAAAAAAAA 就可以了由于不能直接定义0xAAAAAAAA 我们需要一些位运算的小技巧
int a=0xAA<<8; //0xAA00
int c=a|0xAA; //0xAAAA
int d=c<<16|c; //0xAAAAAAAA
等号的操作可以直接利用a == b 等价于 !((a & b)^b)
int allOddBits(int x) {
int a=0xAA<<8;
int c=a|0xAA;
int d=c<<16|c;
return !((x&d)^(d));
}
1.5 negate
/*
* negate - return -x
* Example: negate(1) = -1.
* Legal ops: ! ~ & ^ | + << >>
* Max ops: 5
* Rating: 2
*/
思路
A + ~A = -1 和 A + neg A =0 利用这两个式子我们可以得到 neg A = ~A + 1
int negate(int x)
return ~x+1 ;
}
1.6 isAsciiDigit
* isAsciiDigit - return 1 if 0x30 <= x <= 0x39 (ASCII codes for characters '0' to '9')
* Example: isAsciiDigit(0x35) = 1.
* isAsciiDigit(0x3a) = 0.
* isAsciiDigit(0x05) = 0.
* Legal ops: ! ~ & ^ | + << >>
* Max ops: 15
* Rating: 3
*/
思路
我们先看一下0x39 和 0x30的位级表示
00111001 和 00110000 首先那我们必须满足x>>4==3 然后在满足后4位位于0-9之间这个题用了一些小技巧
x & 0xF保存了x的后四位- 用- A是否为负数来判断后四位的范围
c=~0xA+1实现-A - 判断负数是和
0x8000进行与运算是一个正数
int isAsciiDigit(int x) {
int a=!(x >> 4 ^0x3);
int b=x&0xF;
int c=~0xA+1;
int e=0x80<<4;
int d=!!((b+c)&(e));
return a&d ;
}
1.7 conditional
/*
* conditional - same as x ? y : z
* Example: conditional(2,4,5) = 4
* Legal ops: ! ~ & ^ | + << >>
* Max ops: 16
* Rating: 3
*/
思路
x > 0 return y else return z
我们需要寻找一种方法当x != 0时候 让x变成0xFFFFFFFF
int a=!!(x^0x0); //a=0 if x=0 else a =1
int b=~a+1;
int c=~(y&~b)+1;
int d=~(z&b)+1;
return y+z+c+d 我们最后这样返回,上述代码的含义其实非常简单
如果x!=0 那么 c就会等于-y 我们最后就可以返回z 否则我们就返回y
1.8 isLessOrEqual
* isLessOrEqual - if x <= y then return 1, else return 0
* Example: isLessOrEqual(4,5) = 1.
* Legal ops: ! ~ & ^ | + << >>
* Max ops: 24
* Rating: 3
*/
思路
注意直接用x-y可能会爆int故不能通过这样简单的判断
int a=x>>31&0x1;
int b=y>>31&0x1;
int c1=(a&~b); //表示 x为- y为+
int c2=(~a&b); //表示 x + y -
下面我们计算y-x 这里需要考虑一些情况
y-x >= 0也就是第32位为0flag=y+(~x+1)>>31=0这时候如果c2为1 则表示溢出了 c2为1 的情况我们应该返回0如果c2=0则我们应该返回1y-x <0则flag=1返回0
因此有如下代码
int e=y+(~x+1); // x-y;
int flag=e>>31; //如果flag 和 c2 不同则说明了溢出了
return c1 |(!c2&!flag);
1.9 logicalNeg
/*
* logicalNeg - implement the ! operator, using all of
* the legal operators except !
* Examples: logicalNeg(3) = 0, logicalNeg(0) = 1
* Legal ops: ~ & ^ | + << >>
* Max ops: 12
* Rating: 4
*/
思路
if x!=0 return 0 else return 1 那么问题就变成了如何判断x!=0
我们先看一下~x+1>>31 的情况 只要x!=0 那么他全为-1 只有x=0 的时候为出现0
那么我们用 x |(~x+1>>31) 如果为-1 则表示x!=0 为 0 则表示x=0
int logicalNeg(int x) {
return ((x | (~x +1)) >> 31) + 1;
}
1.10 howManyBits
/* howManyBits - return the minimum number of bits required to represent x in
* two's complement
* Examples: howManyBits(12) = 5
* howManyBits(298) = 10
* howManyBits(-5) = 4
* howManyBits(0) = 1
* howManyBits(-1) = 1
* howManyBits(0x80000000) = 32
* Legal ops: ! ~ & ^ | + << >>
* Max ops: 90
* Rating: 4
*/
思路
本题就是要找到从右向左,最左边的1在第几位然后加上一位符号位即可,如果是负数的话我们对其取反然后是同样的操作那么会有以下几种情况
x 在[0,1]我们需要2位x在[2,3]我们需要3位x在[4,7]我们需要四位- 总结公式 \(2^i\leq x \leqslant 2^{i+1}-1\) 需要
i+2位
对于高16位我们这样进行处理
x=(flag&~x)|(~flag&x); //x为非正数则不变 ,x 为负数 则相当于按位取反
int b16=!!(x>>16) <<4; //如果高16位不为0,则我们让b16=16
x>>=b16; //如果高16位不为0 则我们右移动16位 来看高16位的情况
然后去看高8位下面的处理基本类似
//下面过程基本类似
int b8=!!(x>>8)<<3;
x >>= b8;
int b4 = !!(x >> 4) << 2;
x >>= b4;
int b2 = !!(x >> 2) << 1;
x >>= b2;
int b1 = !!(x >> 1);
x >>= b1;
int b0 = x;
return b0+b1+b2+b4+b8+b16+1;
建议大家手动模拟一下这个过程
1.11 floatScale2
//float
/*
* floatScale2 - Return bit-level equivalent of expression 2*f for
* floating point argument f.
* Both the argument and result are passed as unsigned int's, but
* they are to be interpreted as the bit-level representation of
* single-precision floating point values.
* When argument is NaN, return argument
* Legal ops: Any integer/unsigned operations incl. ||, &&. also if, while
* Max ops: 30
* Rating: 4
*/
思路

1.首先考虑第一种情况
When argument is NaN, return argument
需要先求出exp
int exp = (uf&0x7f800000)>>23; //23-30 这8位
int sign=uf>>31&0x1; //符号位
int frac=uf&0x7FFFFF;
如果exp=255 并且尾数非0 就是NaN 直接return 就好 其次如果frac 全为0 那么则表示无穷大 这两种情况都可以直接return
-
如果
exp=0则表示非规格化数

那么我们直接返回
uf*2就可就是把frac>>1 -
如果
exp!=0 && !=255那么表示规格化数

那么我们的修改就先把exp+1
unsigned floatScale2(unsigned uf) {
unsigned exp = (uf&0x7f800000)>>23;
unsigned sign=uf>>31&0x1;
unsigned frac=uf&0x7FFFFF;
unsigned res;
if(exp==0xFF)return uf;
else if(exp==0){
frac <<= 1;
res = (sign << 31) | (exp << 23) | frac;
}
else{
exp++;
res = (sign << 31) | (exp << 23) | frac;
}
return res;
}
1.12 floatFloat2Int
/*
* floatFloat2Int - Return bit-level equivalent of expression (int) f
* for floating point argument f.
* Argument is passed as unsigned int, but
* it is to be interpreted as the bit-level representation of a
* single-precision floating point value.
* Anything out of range (including NaN and infinity) should return
* 0x80000000u.
* Legal ops: Any integer/unsigned operations incl. ||, &&. also if, while
* Max ops: 30
* Rating: 4
*/
思路
6位IEEE浮点数格式如下
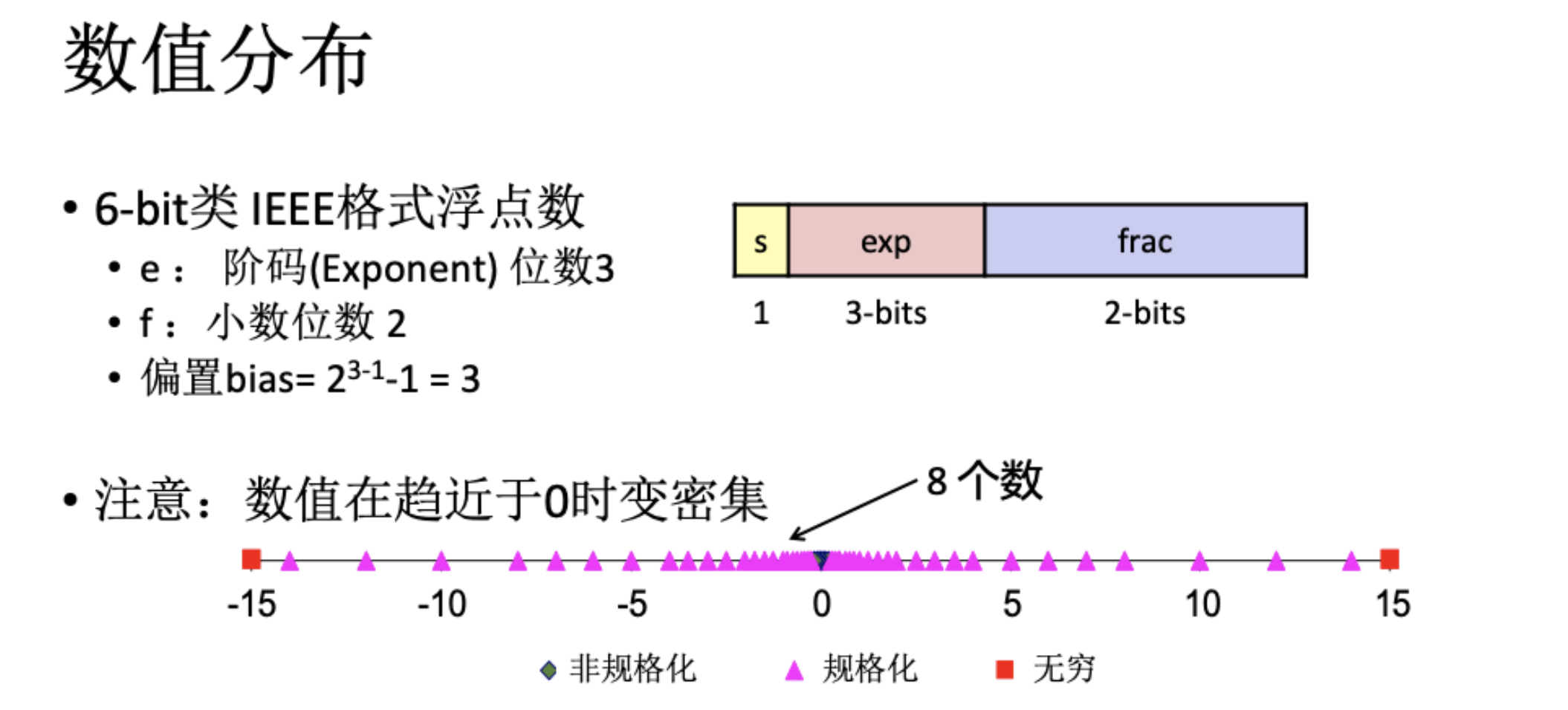
根据上图我们可以分为三种情况
先计算出E=exp-bias
-
如果是小数
E< 0的情况我们直接返回0 -
如果是
exp=255的情况直接返回0x80000000u这里注意如果超范围了也会直接返回0x80000000u因此可以直接用
E>=31来判断 -
如果是规格化数则我们进行正常处理\(V=(-1)^s \times M \times 2^E\)
- 先给尾数补充上省略的1
- 判断
E<23则尾数需要舍去23-E位 - 根据符号位返回就好
int floatFloat2Int(unsigned uf) {
unsigned exp = (uf&0x7f800000)>>23;
int sign=uf>>31&0x1;
unsigned frac=uf&0x7FFFFF;
int E=exp-127;
if(E<0)return 0;
else if(E >= 31){
return 0x80000000u;
}
else{
frac=frac|1<<23;
if(E<23) {//需要舍入
frac>>=(23-E);
}else{
frac <<= (E - 23);
}
}
if (sign)
return -frac;
else
return frac;
}
1.13 floatPower2
/*
* floatPower2 - Return bit-level equivalent of the expression 2.0^x
* (2.0 raised to the power x) for any 32-bit integer x.
*
* The unsigned value that is returned should have the identical bit
* representation as the single-precision floating-point number 2.0^x.
* If the result is too small to be represented as a denorm, return
* 0. If too large, return +INF.
*
* Legal ops: Any integer/unsigned operations incl. ||, &&. Also if, while
* Max ops: 30
* Rating: 4
*/
思路

根据上图我们可以得出几个边界
x>127返回+NANx<-148太小返回0x>=-126规格化数- 否则就是非规格化数
unsigned floatPower2(int x) {
if(x>127){
return 0xFF<<23;
}
else if(x<-148)return 0;
else if(x>=-126){
int exp = x + 127;
return (exp << 23);
} else{
int t = 148 + x;
return (1 << t);
}
}
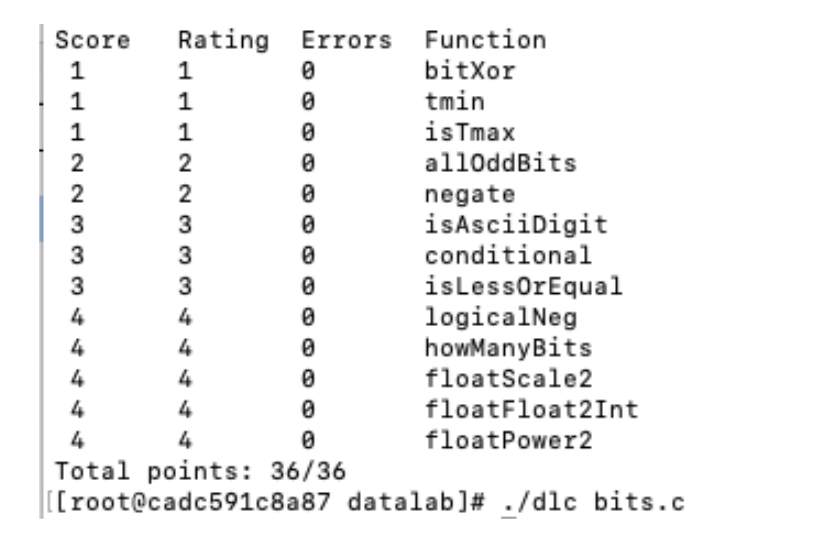
出现上图的结果即为正确