#####废话的开始#####,从今天开始,可能就会多一个话题了,虽然以前在学校也学过数据结构这门课程,但是作为新世纪的90后,还是把学到的东西原原本本还给了老师,有借有还再借不难。其实后续也陆陆续续学习过,但是没有去做很好总结,容易忘记,毕竟作为一个半路出家的码农来说,这个需要好好学习,主要是没怎么写代码,所以基本没用到这些,就算写了代码,好像也用的不多,除非是从事底层开发的小伙伴,不过学会了这个数据结构和算法还是有有很多好处的,具体怎样,请继续往下看。
为什么要写一个数据结构和算法的相关的介绍呢?学这个前至少也要知道自己为什么要学这个东西吧,学好了可以干嘛,可以怎么去学习。此文只是为了更好的从全局去了解数据结构和算法,为后期的学习做一个认知,做一个全局的认知后,对后期的学习会更好,会更加的系统,更加的巩固,对于数据结构和算法的介绍所以也是很重要的,因为我们每做一件事情之前都要知道做这件事的目的,能够带来什么好处,怎么去做,用什么方式做的更好更有效率。不说别的吧,就说对于面试就很有用,看java的源码也有用,越是接触到底层的代码,就越能体现数据结构和算法的重要性。如果你只是满足于调用封装好的代码,那就到此为止,没必要往下看,如果想好好的了解数据结构和算法,就认真的往下看,什么是数据结构和算法,有什么用,有什么魅力。
一、为什么要学数据结构和算法?
其实只要作为一个码代码的程序员来说,写程序的都需要学这个,毕竟:程序 = 数据结构 + 算法 + 程序设计语言
数据结构和算法是程序的灵魂啊,失去灵魂的程序肯定是没精神气的(臃肿,速度慢,消耗资源多)
装逼!强行装逼!!强行一起吹水!!!这点很重要,其实下面的才是重点:
- 算法锻炼自己的逻辑思维;
- 提升代码性能,节省空间复杂度和时间复杂度
- 能够在学习的过程中看的懂源码,能够在什么场景下知道选用更有的算法方案
- 找工作面试,有的甚至要现场写代码,升职加薪
- 一流的程序员搞算法,二流的程序员搞架构,三流的程序员搞业务;
- 很多时候根据公司的场景可以有选择性的时间换空间或者空间换时间,这样就增加了选择
- 更好的理解应用软件和框架,很多知名软件和框架中都大量用了数据结构算法,比如mysql的索引用了b+树,redis的list底层用了跳跃表,理解这些数据结构能更好的帮助我们理解使用这些软件
总之,很重要!很重要!!真的很重要!!!
二、数据结构和算法是什么?
2.1、数据结构介绍
数据结构就是把数据组织起来,为了更方便地使用数据我们为了解决问题,需要将数据保存下来,然后根据数据的存储方式来设计算法实现进行处理,那么数据的存储方式不同就会导致需要不同的算法进行处理。我们希望算法解决问题的效率越快越好,于是我们就需要考虑数据究竟如何保存的问题,这就是数据结构。
数据结构可分为:线性结构和非线性结构。
线性结构:
- 线性结构作为最常用的数据结构,其特点是数据元素之间存在一对一的线性关系
- 线性结构有两种不同的存储结构,即顺序存储结构(数组)和链式存储结构(链表)。顺序存储的线性表称为顺序表,顺序表中的存储元素是连续的
- 链式存储的线性表称为链表,链表中的存储元素不一定是连续的,元素节点中存放数据元素以及相邻元素的地址信息
- 线性结构常见的有:数组、队列、链表和栈.
非线性结构:
非线性结构包括:二维数组,多维数组,广义表,树结构,图结构
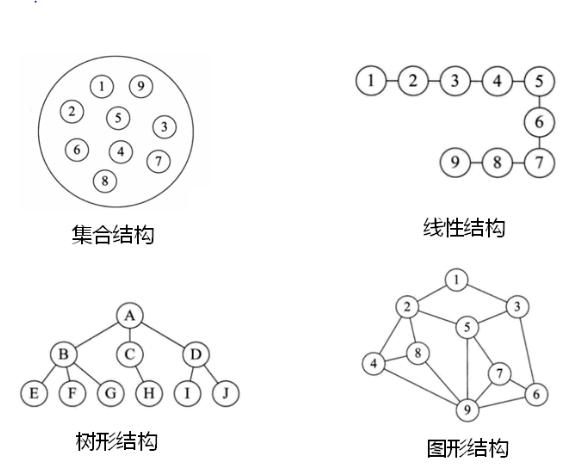
非线性结构可以继续分:集合、树形结构、图状结构
- 集合结构:除了同属于一种类型外,别无其它关系。
- 树形结构:元素之间存在一对多关系。常见类型有:树(有许多特例:二叉树、平衡二叉树、查找树等)
- 图形结构:元素之间存在多对多关系,图形结构中每个结点的前驱结点数和后续结点多个数可以任意。
存储结构表示数据在计算机中的表现形式:
- 顺序存储结构:顺序存储结构将数据存储在地址连续的存储单元里。
- 链接存储结构:链式存储结构将数据存储在任意的存储单元里,通过保存地址的方式找到相关联的数据元素。
- 索引存储结构;在存储数据的同时,简历数据的索引数据,方便对数据进行查询;
- 散列存储结构:通过散列函数对关键字进行计算算出元素的存储地址
2.2、算法介绍
算法(Algorithm)是指解题方案的准确而完整的描述,是一系列解决问题的清晰指令,算法代表着用系统的方法描述解决问题的策略机制。也就是说,能够对一定规范的输入,在有限时间内获得所要求的输出。如果一个算法有缺陷,或不适合于某个问题,执行这个算法将不会解决这个问题。不同的算法可能用不同的时间、空间或效率来完成同样的任务。一个算法的优劣可以用空间复杂度与时间复杂度来衡量。—-算法百度百科
算法是计算机处理信息的本质,因为计算机程序本质上是一个算法来告诉计算机确切的步骤来执行一个指定的任务。一般地,当算法在处理信息时,会从输入设备或数据的存储地址读取数据,把结果写入输出设备或某个存储地址供以后再调用。算法是独立存在的一种解决问题的方法和思想。
其实算法就是解决问题的一种方法或者是思路,所以每个算法都有自己的应用场景,所以很多情况要根据实际情况选择合适的算法或者是设计算法。所以明白算法的原理,至少能够让你在面对不同的场景的时候能够正确的选择哪一种算法,提高效率,节约资源,这都是时间和白花花的银子啊,所以好好学习算法很重要。
算法的五大特性:
- 有穷性(Finiteness):算法的有穷性是指算法必须能在执行有限个步骤之后终止;
- 确切性(Definiteness):算法的每一步骤必须有确切的定义;
- 输入项(Input):一个算法有0个或多个输入,以刻画运算对象的初始情况,所谓0个输入是指算法本身定出了初始条件;
- 输出项(Output):一个算法有一个或多个输出,以反映对输入数据加工后的结果。没有输出的算法是毫无意义的;
- 可行性(Effectiveness):算法中执行的任何计算步骤都是可以被分解为基本的可执行的操作步骤,即每个计算步骤都可以在有限时间内完成(也称之为有效性)
时间复杂度:
算法的时间复杂度是指执行算法所需要的计算工作量。一般来说,计算机算法是问题规模n 的函数f(n),算法的时间复杂度也因此记做。T(n)=Ο(f(n)),因此,问题的规模n 越大,算法执行的时间的增长率与f(n) 的增长率正相关,称作渐进时间复杂度(Asymptotic Time Complexity)。
- 时间频度 一个算法执行所耗费的时间,从理论上是不能算出来的,必须上机运行测试才能知道。但我们不可能也没有必要对每个算法都上机测试,只需知道哪个算法花费的时间多,哪个算法花费的时间少就可以了。并且一个算法花费的时间与算法中语句的执行次数成正比例,哪个算法中语句执行次数多,它花费时间就多。一个算法中的语句执行次数称为语句频度或时间频度。记为T(n)。
- 时间复杂度 在刚才提到的时间频度中,n称为问题的规模,当n不断变化时,时间频度T(n)也会不断变化。但有时我们想知道它变化时呈现什么规律。为此,我们引入时间复杂度概念。 一般情况下,算法中基本操作重复执行的次数是问题规模n的某个函数,用T(n)表示,若有某个辅助函数f(n),使得当n趋近于无穷大时,T(n)/f(n)的极限值为不等于零的常数,则称f(n)是T(n)的同数量级函数。记作T(n)=O(f(n)),称O(f(n)) 为算法的渐进时间复杂度,简称时间复杂度。
- 在各种不同算法中,若算法中语句执行次数为一个常数,则时间复杂度为O(1),另外,在时间频度不相同时,时间复杂度有可能相同,如T(n)=n^2+3n+4与T(n)=4n^2+2n+1它们的频度不同,但时间复杂度相同,都为O(n^2)。 按数量级递增排列,常见的时间复杂度有:常数阶O(1),对数阶O(log2n),线性阶O(n), 线性对数阶O(nlog2n),平方阶O(n^2),立方阶O(n^3),…, k次方阶O(n^k),指数阶O(2^n)。随着问题规模n的不断增大,上述时间复杂度不断增大,算法的执行效率越低。
常见的时间复杂度:
| 执行次数函数举例 | 阶 | 非正式术语 |
| 12 | O(1) | 常数阶 |
| 2n+3 | O(n) | 线性阶 |
| 3n^2+2n+1 | O(n^2) | 平方阶 |
| 5log2n+20 | O(logn) | 对数阶 |
| 2n+3nlog2n+19 | O(nlogn) | nlogn阶 |
| 6n^3+2n^2+3n+4 | O(n^3) | 立方阶 |
| 2^n | O(2^n) | 指数阶 |
常见时间复杂度之间的关系,所消耗的时间从小到达:O(1) < O(logn) < O(n) < O(nlogn) < O(n^2) < O(n^3) < O(2^n) < O(n!) < O(n^n)
空间复杂度:
算法的空间复杂度是指算法需要消耗的内存空间。其计算和表示方法与时间复杂度类似,一般都用复杂度的渐近性来表示。同时间复杂度相比,空间复杂度的分析要简单得多.
算法的空间复杂度(Space Complexity)S(n)定义为该算法所耗费的存储空间,它也是问题规模n的函数。渐近空间复杂度也常常简称为空间复杂度。记为S(n)=O(f(n))
空间复杂度(Space Complexity)是对一个算法在运行过程中临时占用存储空间大小的量度。一个算法在计算机存储器上所占用的存储空间,包括存储算法本身所占用的存储空间,算法的输入输出数据所占用的存储空间和算法在运行过程中临时占用的存储空间这三个方面。算法的输入输出数据所占用的存储空间是由要解决的问题决定的,是通过参数表由调用函数传递而来的,它不随本算法的不同而改变。存储算法本身所占用的存储空间与算法书写的长短成正比,要压缩这方面的存储空间,就必须编写出较短的算法。算法在运行过程中临时占用的存储空间随算法的不同而异,有的算法只需要占用少量的临时工作单元,而且不随问题规模的大小而改变,我们称这种算法是“就地\”进行的,是节省存储的算法,有的算法需要占用的临时工作单元数与解决问题的规模n有关,它随着n的增大而增大,当n较大时,将占用较多的存储单元。
当然评价算法的好坏不仅仅是算法的时间复杂度和空间复杂度,比如还有正确性,可读性,键值性等,明白了时间复杂度和空间复杂度,就知道什么情况下什么场景可以考虑时间换空间,或者空间换时间了,这些都是根据实际情况而定的,没有最好的算法,只有更适合的某些场景的算法。
算法中常用的分析方法:递推法、递归法、穷举法、贪心算法、分治法、动态规划法、迭代法、分支界限法、回溯法。
算法的分类:
算法可大致分为基本算法、数据结构的算法、数论与代数算法、计算几何的算法、图论的算法、动态规划以及数值分析、加密算法、排序算法、检索算法、随机化算法、并行算法,厄米变形模型,随机森林算法。算法可以宏泛的分为三类:
- 有限的,确定性算法 这类算法在有限的一段时间内终止。他们可能要花很长时间来执行指定的任务,但仍将在一定的时间内终止。这类算法得出的结果常取决于输入值。
- 有限的,非确定算法 这类算法在有限的时间内终止。然而,对于一个(或一些)给定的数值,算法的结果并不是唯一的或确定的。
- 无限的算法 是那些由于没有定义终止定义条件,或定义的条件无法由输入的数据满足而不终止运行的算法。通常,无限算法的产生是由于未能确定的定义终止条件 。
三、如何学习数据结构和算法?
- 明确目的,为啥要学习数据结构和算法–提供动力
- 明确方向,明白自己要学习数据结构和算法中的哪些内容
- 动手,动手,动手,懂原理,代码实现,还有最重要的一步就是总结和分享
- 明白每个数据结构和算法的来历,特点,优缺点和使用场景
- 可以去看一些java中的源码,想想别人优秀代码的实现,为什么要这么写,还有更优的方案吗?
- 当然资源也很重要:可以听课,网上课程很多,看书籍《算法导论》《数学之美》等,网络资源:算法可视化网站(中文版)
- 可以适度的刷题,这样可以强化记忆
- 学会提出问题,解决问题,记录问题,实现解决方案
比如常见的一些数据结构和算法:
- 10 个数据结构:数组、链表、栈、队列、散列表、二叉树、堆、跳表、图、Trie 树;
- 10 个算法:递归、排序、二分查找、搜索、哈希算法、贪心算法、分治算法、回溯算法、动态规划、字符串匹配算法
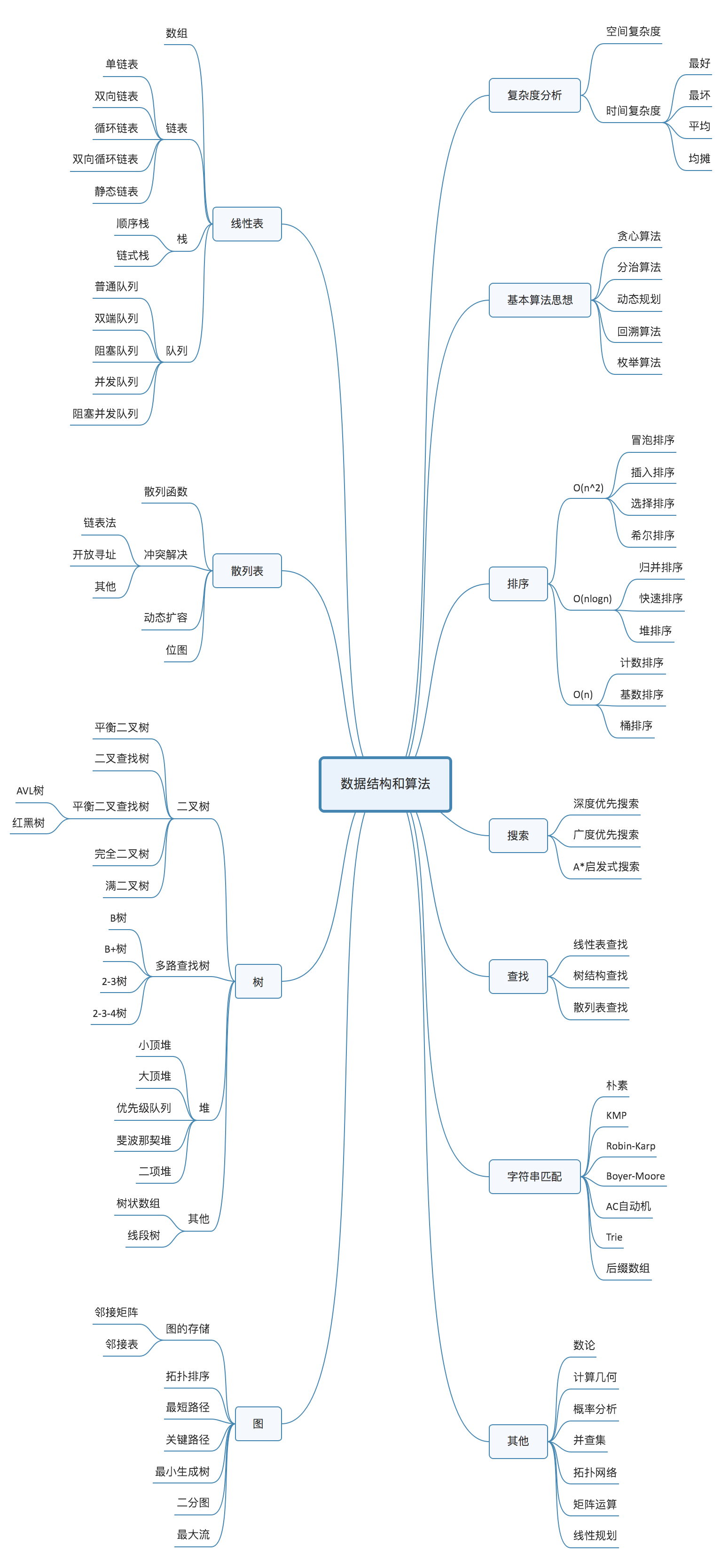
数据结构和算法知识结构思维导图(引用优秀博文,见参考文章):
参考:
https://www.cnblogs.com/54chensongxia/p/11448695.html
https://www.cnblogs.com/chjxbt/p/10967968.html
https://baike.baidu.com/item/%E7%AE%97%E6%B3%95/209025
https://www.cnblogs.com/songQQ/archive/2009/10/20/1587122.html




