今天的主角是指数分布,由此导出\(\Gamma\)分布,同样,读者应尝试一边阅读,一边独立推导出本文的结论。由于本系列为我独自完成的,缺少审阅,如果有任何错误,欢迎在评论区中指出,谢谢!
目录
- Part 1:指数分布的参数估计
- Part 2:独立同分布指数分布之和与\(\Gamma\)分布
- Part 3:\(\Gamma\)分布与其他分布
Part 1:指数分布的参数估计
指数分布是单参数分布族,总体\(X\sim E(\lambda)\)有时也记作\(\mathrm{Exp}(\lambda)\),此时的总体密度函数为
\[f(x)=\lambda e^{-\lambda x}I_{x>0}. \]
现寻找其充分统计量,样本联合密度函数为
\[\begin{aligned} f(\boldsymbol{x})&=\lambda^n\exp\left\{-\lambda\sum_{j=1}^n x_j \right\}I_{x_1>0}\cdots I_{x_n>0}\\ &=\lambda^ne^{-n\lambda \bar x}I_{x_{(1)}>0}, \end{aligned} \]
由因子分解定理,取
\[g(\bar x,\lambda)=\lambda^ne^{-n\lambda \bar x},\quad h(\boldsymbol{x})=I_{x_{(1)}>0}, \]
可以得到\(\bar X\)是\(\lambda\)的充分统计量。但是指数分布的参数并非均值,而是均值的倒数,所以对\(\bar X\)也有
\[\mathbb{E}(\bar X)=\mathbb{E}(X)=\frac{1}{\lambda}. \]
注意,千万不要想当然地认为期望和一般的函数之间是可交换的,即一般来说\(\mathbb{E}[f(X)]\ne f[\mathbb{E}(X)]\),所以你不能认为\(\bar X^{-1}\)就是\(\lambda\)的无偏估计量。
每到此时,我就想举对数正态分布的例子:\(X\sim N(0,\sigma^2)\),求\(e^{X}\)的期望。显然有
\[\begin{aligned} \mathbb{E}(e^{X})&=\int_{-\infty}^\infty e^x\frac{1}{\sqrt{2\pi\sigma^2}}\exp\left\{-\frac{x^2}{2\sigma^2} \right\}\mathrm{d}x\\ &=\int_{-\infty}^\infty \frac{1}{\sqrt{2\pi\sigma^2}}\exp\left\{-\frac{x^2-2\sigma^2x}{2\sigma^2} \right\}\mathrm{d}x\\ &=e^{\frac{\sigma^2}{2}}\int_{-\infty}^\infty \frac{1}{\sqrt{2\pi\sigma^2}}\exp\left\{-\frac{(x-\sigma^2)^2}{2\sigma^2} \right\}\mathrm{d}x\\ &=e^{\frac{\sigma^2}{2}}. \end{aligned} \]
最后一个等号处,积分是\(N(\sigma^2,\sigma^2)\)的密度函数全积分为1。这说明
\[\mathbb{E}(e^{X})=e^{\frac{\sigma^2}{2}}\ne 1=e^{\mathbb{E}(X)}. \]
同样,也能告诉我们股票的波动率越大,期望收益也越大。
但是,用\(\bar X^{-1}\)总是有一定道理的,至少在量级上保持了跟待估参数的一致性。如果我们要进行无偏调整,则需要求出\(\bar X\)的具体密度。不妨设\(T=\sum_{j=1}^n X_j\),则\(T=n\bar X\),如果我们能求出\(T\)的分布,也一样能得出\(\bar X^{-1}\)的期望。
Part 2:独立同分布指数分布之和与\(\Gamma\)分布
为求\(T\)的分布,引入一个Jacobi行列式为1的线性变换:
\[\left\{\begin{array}l Y_{1} = X_{1}, \\ Y_{2}=X_{2},\\ \vdots \\ Y_{n-1}=X_{n-1}, \\ Y_{n}=X_{1}+\cdots+ X_{n}. \end{array}\right. \]
则\((Y_{1},\cdots,Y_{n})\)的联合密度函数为
\[\begin{aligned} f_{Y}(\boldsymbol{y})&=f_X(y_{1},\cdots,y_{n-1},y_n-y_{n-1}-\cdots-y_1)\\ &=\lambda^n\exp\left\{-\lambda\left[\sum_{j=1}^{n-1}y_j+\left(y_n-\sum_{j=1}^{n-1}y_j \right) \right] \right\}I_{y_1>0}\cdots I_{y_{n-1}>0}I_{y_n>\sum_{j=1}^{n-1}y_j}\\ &=\lambda^n e^{-\lambda y_n}I_{y_1>0}\cdots I_{y_{n-1}>0}I_{y_n>\sum_{j=1}^{n-1}y_j}. \end{aligned} \]
接下来要依次对\(y_1,\cdots,y_{n-1}\)作积分,为方便计,记
\[\mathcal B_k=y_n-\sum_{j=k}^{n-1}y_j,\quad k=1,2,\cdots,n-1,\\ \mathcal B_{k+1}-\mathcal B_{k}=y_k. \]
现在,\(y_1\)的积分范围是\((0,y_n-y_{n-1}-\cdots-y_2)=(0,\mathcal B_2)\),即
\[f_{Y_2,\cdots,Y_n}(y_2,\cdots,y_n)=\lambda^ne^{-\lambda y_n}\mathcal B_2I_{y_2>0}\cdots I_{y_{n-1}>0}I_{\mathcal B_2>0}. \]
再对\(y_2\)积分,其积分范围是\((0,\mathcal B_3)\),即
\[\begin{aligned} &\quad f_{Y_3,\cdots,Y_n}(y_3,\cdots,y_n)\\ &=\lambda ^ne^{-\lambda y_n}\int_{0}^{\mathcal B_3}\mathcal B_2\mathrm{d}y_2\\ &=\lambda^ne^{-\lambda y_n}\int_0^{\mathcal B_3}(\mathcal B_3-y_2)\mathrm{d}y_2\\ &=\lambda^n e^{-\lambda y_n}\cdot\frac{\mathcal B_3^2}{2}I_{y_3>0}\cdots I_{y_{n-1}>0}I_{\mathcal B_3>0}. \end{aligned} \]
继续下去的步骤就很机械了,对\(y_3\)积分时积分范围是\((0,\mathcal B_4)\),所以
\[\begin{aligned} &\quad f_{Y_4,\cdots,Y_n}(y_4,\cdots,y_n)\\ &=\frac{1}{2}\lambda^n e^{-\lambda y_n}\int_0^{\mathcal B_4}[\mathcal B_4-y_3]^2\mathrm{d}y_3\\ &=\frac{1}{2}\lambda^n e^{-\lambda y_n}\int_0^{\mathcal B_4}[\mathcal B_4-y_3]^2\mathrm{d}(\mathcal B_4-y_3)\\ &=\frac{1}{2\cdot 3}\lambda^n e^{-\lambda y_n}\mathcal B_4^3I_{y_4>0}\cdots I_{y_{n-1}>0}I_{\mathcal B_4>0}. \end{aligned} \]
将这个过程一直进行下去,容易得到
\[f_{Y_{n-1},Y_n}(y_{n-1},y_n)=\frac{1}{(n-2)!}\lambda^ne^{-\lambda y_n}\mathcal B_{n-1}^{n-2}I_{y_{n-1}>0}I_{y_n>y_{n-1}}, \]
进行最后一次积分就能得到\(T\)的密度函数为
\[f_T(x)=\frac{1}{(n-1)!}\lambda^ne^{-\lambda x}x^{n-1}. \]
这里有一个稍微有点耍赖的技巧。如果你不想一个个积分,而又记住了指数分布和的密度函数形式,则可以用数学归纳法验证指数分布和的密度函数恰有如此的形式。
读者可以自行用数学归纳法计算一遍,这个计算量是比较小的。
同样,我们以后会经常跟这个密度函数打交道。因为阶乘只适用于整数,将其解析延拓到\(\mathbb{R}^+\)上有\((n-1)!=\Gamma(n)\),注意到其核为\(e^{-\lambda x}x^{n-1}\),对于任意\(n>0,\lambda >0\),有
\[\int_0^{\infty}e^{-\lambda x}x^{n-1}\mathrm{d}x=\int_0^{\infty}\frac{1}{\lambda^n}e^{-\lambda x}(\lambda x)^{n-1}\mathrm{d}(\lambda x)=\frac{\Gamma(n)}{\lambda ^n}, \]
所以其正则化因子为\(\frac{\lambda^n}{\Gamma(n)}\)。现在我们可以正式给出\(\Gamma\)分布的定义:称\(X\sim\Gamma(n,\lambda)\),如果\(X\)具有如下的密度函数:
\[p(x)=\frac{\lambda^n}{\Gamma(n)}x^{n-1}e^{-\lambda x}. \]
当\(n\)为整数时,\(\Gamma(n)=(n-1)!\)。同时,我们得到一个重要结论:若\(X_1,\cdots,X_n\stackrel{\mathrm{i.i.d.}}\sim E(\lambda)\),则
\[T=\sum_{j=1}^n X_j\sim \Gamma(n,\lambda). \]
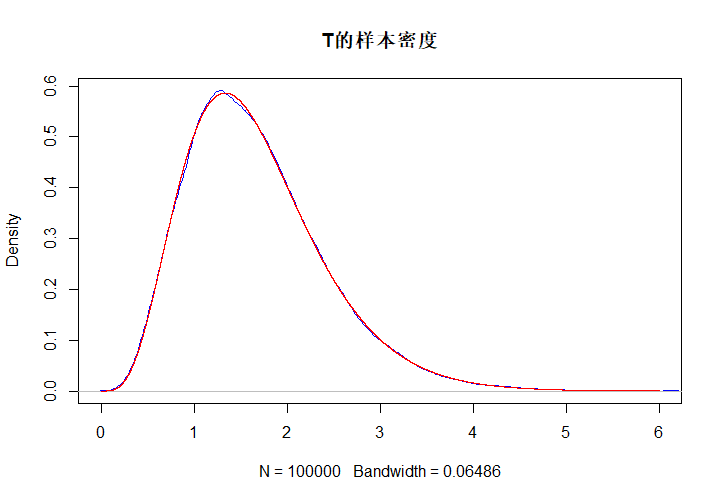
Tlst <- c()
for (i in 1:100000){
Tlst[i] <- sum(rexp(5, 3)) # T为5个E(3)样本之和
}
plot(density(Tlst), main = "T的样本密度", col = "blue", xlim = c(0, 6))
xlst <- seq(0, 6, 0.00001)
ylst <- dgamma(xlst, 5, 3)
lines(xlst, ylst, col = "red")
由于\(\Gamma\)分布核函数的特点,其期望和方差也是容易求出的。现设\(X\sim \Gamma(n)\),则
\[\mathbb{E}(X)=\int_0^{\infty}\frac{\lambda^n}{\Gamma(n)}x^ne^{-\lambda x}\mathrm{d}x=\frac{\Gamma(n+1)}{\lambda\Gamma(n)}\int_0^{\infty}\frac{\lambda^{n+1}}{\Gamma(n+1)}x^{n+1-1}e^{-\lambda x}\mathrm{d}x=\frac{n}{\lambda}. \]
这说明\(n\)越大\(X\)的期望越大,\(\lambda\)越大\(X\)的期望越小,如果将其视为独立指数分布的和也能得到这个结论。
\[\mathbb{E}(X^2)=\frac{\Gamma(n+2)}{\lambda^2\Gamma(n)}=\frac{n(n+1)}{\lambda^2},\\ \mathbb{D}(X)=\mathbb{E}(X^2)-[\mathbb{E}(X)]^2=\frac{n}{\lambda^2}. \]
现在回到正题,计算指数分布均值倒数\(\bar X^{-1}\)的期望,先计算\(T^{-1}\)的期望,容易计算得到
\[\mathbb{E}(T^{-1})=\int_0^{\infty}\frac{\lambda ^n}{\Gamma(n)}x^{n-2}e^{-\lambda x}\mathrm{d}x=\frac{\lambda\Gamma(n-1)}{\Gamma(n)}=\frac{\lambda}{n-1}, \]
因此自然有
\[\mathbb{E}\left(\frac{1}{\bar X} \right)=\mathbb{E}\left(\frac{n}{T} \right)=\frac{\lambda n}{n-1}. \]
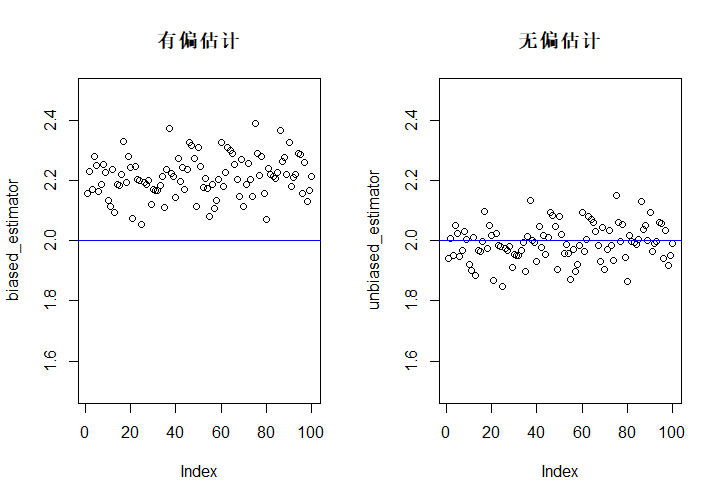
因此,\(\bar X^{-1}\)只是\(\lambda\)的渐进无偏估计,可以对它经过无偏处理得到无偏估计:
\[\hat\lambda(\boldsymbol{X})=\frac{n-1}{n\bar X}. \]
下面进行\(\hat \lambda\)的有偏估计、无偏估计的模拟计算,从指数分布\(E(2)\)中抽样。为了体现出区别,图中的每一个点都是100个估计量的平均值。
rm(list = ls())
unbiased_estimator <- c()
biased_estimator <- c()
for (j in 1:100){
meanlst <- c()
for (i in 1:100){
samples <- rexp(10, 2) # 每次产生10个样本计算均值
meanlst[i] <- 1/mean(samples)
}
biased_estimator[j] <- mean(meanlst)
unbiased_estimator[j] <- 9/10*biased_estimator[j]
}
split.screen(c(1, 2))
screen(1)
plot(biased_estimator, main = "有偏估计", ylim = c(1.5, 2.5))
abline(h = 2, col = "blue")
screen(2)
plot(unbiased_estimator, main = "无偏估计", ylim = c(1.5, 2.5))
abline(h = 2, col = "blue")
Part 3:\(\Gamma\)分布与其他分布
\(\Gamma\)分布与许多分布具有紧密的联系(中心极限定理这种与正态分布的联系就不说了)。与指数分布的联系是显然的:\(\Gamma(1,\lambda)\)就是\(E(\lambda)\),这点从上面的推导可以得出。
需要注意一点:指数分布的参数是其尺度参数。什么意思呢?对于\(X\sim E(\lambda)\),它的分布函数是\(F(x)=1-e^{-\lambda x}\),对其作伸缩变换\(aX\),有
\[F_{aX}(x)=\mathbb{P}(aX<x)=F\left(\frac{x}{a} \right)=1- e^{-\frac{\lambda x}{a}}, \]
对比\(F(x)\)的形式,发现\(aX\sim E(\lambda /a)\),这就代表伸缩变换不改变指数分布的性质,所以说指数分布的参数是其尺度参数。既然\(\Gamma\)分布是指数分布的直接推广,则\(\Gamma\)分布也具有这样的性质:若\(X\sim \Gamma(n,\lambda)\),则
\[aX\sim \Gamma\left(n,\frac{\lambda }{a} \right). \]
这样的变换不改变数量参数\(n\),这也是指数分布中得到的直接推广结论。
还记得正态分布的衍生分布——\(\chi^2(n)\)分布吗?之前,因为卡方分布的密度函数过于复杂,不好记忆,所以我们跳过了,但了解过\(\Gamma\)分布的密度函数后再回看卡方分布,就会有一种熟悉感。
对于\(X\sim \chi^2(n)\),其密度函数为
\[p(x)=\frac{1}{2^{n/2}\Gamma(n/2)}x^{\frac{n}{2}-1}e^{-\frac{x}{2}}, \]
可以看到,它的核刚好是\(e^{-x}\)的某次方,乘以\(x\)的某次方形式,前面的正则化系数由核决定,因此,\(\chi^2(n)\)分布本质上也是\(\Gamma\)分布的一种特例,即
\[X\sim \Gamma\left(\frac{n}{2},\frac{1}{2} \right). \]
这样,再记忆\(\chi^2(n)\)分布的密度函数就会显得容易一些了。另外,如果\(2n\)是整数,也可以通过\(\Gamma\)分布的伸缩变换将其变成卡方分布:
\[X\sim \Gamma(n,\lambda)\Rightarrow 2\lambda X\sim \Gamma\left(n,\frac{1}{2} \right)=\chi^2(2n),\\ X\sim E(\lambda)\Rightarrow 2\lambda X\sim \chi^2(2). \]
最后,由于我们接下来要进入离散分布的参数估计,在这里也给出一个\(\Gamma\)分布与泊松分布的联系,这个联系在随机过程中会发挥一定的作用,其证明在数理统计中倒不是特别重要。
若\(N\)定义为满足下列条件的\(n\)值:\(X_1,X_2,\cdots\stackrel{\mathrm{i.i.d.}}\sim E(\lambda)\),
\[\sum_{j=1}^n X_j\le 1<\sum_{j=1}^{n+1}X_j \]
则\(N\sim P(\lambda)\)。
下面给出这个定理的证明,其中的思想可以学习。
设\(\sum_{j=1}^k X_j\)的密度函数为\(p_k(x)\),则由于\(\sum _{j=1}^k X_j\sim \Gamma(k,\lambda)\),所以
\[p_k(x)=\frac{\lambda^k}{\Gamma(n)}x^{k-1}e^{-\lambda x}. \]
由全概率公式(连续形式),
\[\begin{aligned} &\quad \mathbb{P}(N=k)\\ &=\mathbb{P}\left(\sum_{j=1}^kX_i\le 1,\sum_{j=1}^{k+1}X_i>1 \right)\\ &=\int_0^1\mathbb{P}\left(\sum_{j=1}^{k+1} X_j>1\bigg|\sum_{j=1}^k X_i=x \right)p_k(x)\mathrm{d}x\\ &=\int_0^1\mathbb{P}(X_{k+1}>1-x)p_k(x)\mathbb{d}x\\ &=\int_0^1e^{-\lambda {(1-x)}}\frac{\lambda^k}{(k-1)!}x^{k-1}e^{-\lambda x}\mathrm{d}x\\ &=\frac{\lambda^k e^{-\lambda}}{(k-1)!}\int_0^1 x^{k-1}\mathrm{d}x\\ &=\frac{\lambda^k}{k!}e^{-\lambda}. \end{aligned} \]
这是泊松分布的分布列,故\(N\sim P(\lambda)\)。
在上面两篇文章中,将连续分布的点估计进行了详细的讨论,并引出了次序统计量的分布,介绍了\(\Gamma\)分布与\(\beta\)分布。接下来,我们将转向离散型分布的参数点估计,看看离散形式下因子分解定理应当如何使用。