动态规划中初识状态压缩（入门）_其他

想必很多人还不知道动态规划是可以状态压缩的吧，通俗的讲就是把维数变小，一般就是把二维数组降为一维。维数变小意味着空间变小，速度还不变，不用空间换时间，这就是状态压缩的强大之处。

以leetcode64题最小路径和为例，带大家一步一步见识一下状态压缩这个小技巧

题意：给定一个包含非负整数的 m x n 网格 grid ，请找出一条从左上角到右下角的路径，使得路径上的数字总和为最小

说明：每次只能向下或者向右移动一步

示例1

输入：grid = [[1,3,1],[1,5,1],[4,2,1]]

输出：7

解释：因为路径 1→3→1→1→1 的总和最小

函数名：

public int minPathSum(int[][] grid)

题目的最基本的状态转移方程是
dp[i][j] = Math.min(dp[i – 1][j], dp[i][j – 1]) + grid[i][j];

意思是如果我们在i, j 这个位置的话从可以从两个方向推出dp[i][j]的值，题目说明了每次只能向下或者向右移动一步，如下图

完整代码如下

class Solution {
    public int minPathSum(int[][] grid) {
        if (grid.length == 0) return 0;
        int n = grid.length;
        int m = grid[0].length;
        int[][] dp = new int[n][m];
        dp[0][0] = grid[0][0];
        //初始化
            //从（0，0）一直向下走
        for (int i = 1; i < n; i++)
            dp[i][0] = dp[i - 1][0] + grid[i][0];
            //从（0，0）一直向右走
        for (int j = 1; j < m; j++)
            dp[0][j] = dp[0][j - 1] + grid[0][j];

        //状态转移
        for (int i = 1; i < n; i++) 
            for (int j = 1; j < m; j++) 
                dp[i][j] = Math.min(dp[i - 1][j], dp[i][j - 1]) + grid[i][j];
        return dp[n - 1][m - 1];
    }
}

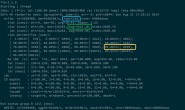
上面的测试用例运行后的dp数组如下

上面的代码很直观吧

下面的代码是为了推出状态压缩而写的，原理和上面一样，只是上面的dp[0][0]换成下面的dp[1][1]

我这样子写不是说要这样子做，只是为了方便大家理解状态压缩而已，基本思路完全没有变

先贴出dp数组结果如下

代码如下

class Solution {
    public int minPathSum(int[][] grid) {
        if (grid.length == 0) return 0;
        int n = grid.length;
        int m = grid[0].length;
        int[][] dp = new int[n + 1][m + 1];
        //初始化
        for (int i = 0; i <= n; i++)
            dp[i][0] = Integer.MAX_VALUE;
        dp[1][1] = grid[0][0];
        //初始状态
            //从（1，1）一直往右走
        for (int j = 2; j <= m; j++)
            dp[1][j] = dp[1][j - 1] + grid[0][j - 1];

        //状态转移
        for (int i = 2; i <= n; i++) 
            for (int j = 1; j <= m; j++) 
                dp[i][j] = Math.min(dp[i - 1][j], dp[i][j - 1]) + grid[i - 1][j - 1];
        return dp[n][m];
    }
}

接下来开始进行状态压缩

把二维降为一维结果如下,采用的是直接投影的方法

投影也就是直接把dp[i][j]中i所在的那一维去掉

代码的转变过程如下

由

dp[i][j] = Math.min(dp[i - 1][j], dp[i][j - 1]) + grid[i - 1][j - 1]

变成

dp[j] = Math.min(dp[j], dp[j - 1]) + grid[i - 1][j - 1]

解释一下上面为什么这样子就完成了

想要求出dp[i][j]需要先求出dp[i – 1][j]和dp[i][j – 1]

我们发现二维的dp[i – 1][j]映射成了一维的dp[j],dp[i][j – 1]映射成了dp[j – 1]

所需要的信息都能直接用一维来表示

哪怕dp[j]被覆盖了也没事，原因看下图

所以

dp[j] = Math.min(dp[j], dp[j - 1]) + grid[i - 1][j - 1]

完整代码如下：

class Solution {
    public int minPathSum(int[][] grid) {
        if (grid.length == 0) return 0;
        int n = grid.length;
        int m = grid[0].length;
        int[] dp = new int[m + 1];
        //初始化
        dp[0] = Integer.MAX_VALUE;
        dp[1] = grid[0][0];
        //从（1，1）一直向右走  真的只是把上面的代码中dp[i][j]的i那一维去掉
        for (int j = 2; j <= m; j++)
            dp[j] = dp[j - 1] + grid[0][j - 1];
        //这里也是直接去掉i中的那一维
        for (int i = 2; i <= n; i++) 
            for (int j = 1; j <= m; j++) 
                dp[j] = Math.min(dp[j], dp[j - 1]) + grid[i - 1][j - 1];
        return dp[m];
    }
}

这题到这里也就结束了

这题的状态压缩之所以简单是因为没有多个元素映射到同一个位置

如果如下图所示的话